算法与数据结构面试题(1)-把二元查找树转变成排序的双向链表
学习网址:http://blog.csdn.net/v_july_v/article/details/5934051
题目
把二元查找树转变成排序的双向链表:
输入一棵二元查找树,将该二元查找树转换成一个排序的双向链表。
要求不能创建任何新的结点,只调整指针的指向。
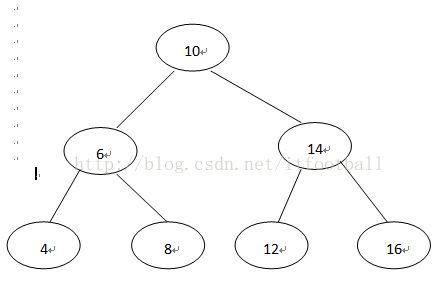
转换成双向链表
4=6=8=10=12=14=16。
首先我们定义的二元查找树 节点的数据结构如下:
struct BSTreeNode
{
int m_nValue; // value of node
BSTreeNode *m_pLeft; // left child of node
BSTreeNode *m_pRight; // right child of node
};个人解题思路
1.首先了解什么是二元查找树以及其特性。
2.存储二元查找树的存储结构
3.中序遍历二元查找树,会得到期望的由小到大的顺序。
4.调整左右指针,将其分别指向前面元素和后面元素。第一个元素的左元素为null,最后一个元素的右元素为null。
解完。
第一步
百度或google一下就知道:
二元查找树: 它首先要是一棵二元树,在这基础上它或者是一棵空树;或者是具有下列性质的二元树: (1)若左子树不空,则左子树上所有结点的值均小于它的根结点的值; (2)若右子树不空,则右子树上所有结点的值均大于它的根结点的值; (3)左、右子树也分别为二元查找树
第二步
存储结构采用数组的形式:第一个位置存储根节点,左右节点的形式为2i+1,2i+2。
int[] bsTree = {10,6,14,4,8,12,16};然后根据该数组得到根节点BSTreeNode。
第三步
中序遍历:中序遍历首先遍历左子树,然后访问根结点,最后遍历右子树。在遍历左、右子树时,仍然先遍历左子树,再访问根结点,最后遍历右子树。
中序遍历后得到的数组为{4,6,8,10,12,14,16}
第四部
调整指针
代码
(java实现)
public class BSTreeNode {
int value; // value of node
BSTreeNode left; // left child of node
BSTreeNode right; // right child of node
public int getValue() {
return value;
}
public void setValue(int value) {
this.value = value;
}
public BSTreeNode getLeft() {
return left;
}
public void setLeft(BSTreeNode left) {
this.left = left;
}
public BSTreeNode getRight() {
return right;
}
public void setRight(BSTreeNode right) {
this.right = right;
}
@Override
public String toString() {
return "BSTreeNode [value=" + value + "]";
}
}
public class Problem1 {
static BSTreeNode[] sortedNode;
int index = 0;
// 由输入的值的数组得到根节点
private BSTreeNode step2(int[] bsTree, int begin) {
int lIndex = 2 * begin + 1;
int rIndex = 2 * begin + 2;
int length = bsTree.length;
BSTreeNode rootNode = new BSTreeNode();
rootNode.setValue(bsTree[begin]);
if (lIndex < length) {
rootNode.setLeft(step2(bsTree, lIndex));
}
if (rIndex < length) {
rootNode.setRight(step2(bsTree, rIndex));
}
return rootNode;
}
// 中序排序
void step3(BSTreeNode rootNode) {
if (rootNode == null)
return;
step3(rootNode.left);
sortedNode[index++] = rootNode;
step3(rootNode.right);
}
// 指针变换
void step4() {
for (int i = 0; i < sortedNode.length; i++) {
BSTreeNode node = sortedNode[i];
node.setLeft(i - 1 > 0 ? sortedNode[i - 1] : null);
node.setRight(i + 1 < sortedNode.length ? sortedNode[i + 1] : null);
}
BSTreeNode firstNode = sortedNode[0];
System.out.println("--");
}
public static void main(String[] args) {
Problem1 p1 = new Problem1();
// step2
int[] bsTree = { 10, 6, 14, 4, 8, 12, 16 };
sortedNode = new BSTreeNode[bsTree.length];
BSTreeNode rootNode = p1.step2(bsTree, 0);
p1.step3(rootNode);
for (int i = 0; i < sortedNode.length; i++) {
System.out.println("第" + i + "节点的值为" + sortedNode[i]);
}
p1.step4();
System.out.println("Done");
}
}
输出
第0节点的值为BSTreeNode [value=4]
第1节点的值为BSTreeNode [value=6]
第2节点的值为BSTreeNode [value=8]
第3节点的值为BSTreeNode [value=10]
第4节点的值为BSTreeNode [value=12]
第5节点的值为BSTreeNode [value=14]
第6节点的值为BSTreeNode [value=16]
--
Done