点的旋转（4）：四元数的乘法

前言

同样的，跟前面一眼四元数的乘法也代表了旋转，四元数的积有多种定义，这里我们只讲被用在旋转操作的上积 —— 矢量积

矢量积

对于两个四元数q，p：
$q=w_1+x_{1}i+y_{1}j+z_{1}k$
$p=w_2+x_{2}i+y_{2}j+z_{2}k$
我们来看q右乘p，按照分配律
$qp=(w_1\ast w_2-x_1\ast x_2-y_1\ast y_2-z_1\ast z_2)+$
$$(x_1\ast w_2+w_1\ast x_2+z_1\ast y_2-z_1\ast y_2)i+$$$$(y_1\ast w_2+w_1\ast y_2+z_1\ast x_2-x_1\ast z_2)j+$$$$(z_1\ast w_2+w_1\ast z_2+x_1\ast y_2-x_2\ast y_1)k+$$
按照同样算法算pq结果是等于-qp的
也就是
$pq=-qp$

旋转

重新审视qp
（1）q右乘p，我们将q作为一个旋转操作，作用于某个值p上
qp即为：p被q按照右手法则变换
（2）p左乘q，我们将p作为一个旋转操作，作用于某个值q上
qp即为：q被p按照左手法则变换

如何旋转一个三维空间的点呢？
现在，假设我们这里有一个旋转操作q，和一个三维坐标v
我们将v看作w = 0处的一个四元数p
$p=(0,v)$
记 $t=qp$
经过一次旋转后 $w_t$ 不为0了，这在三维空间看起来已经变形了
为什么呢，因为一次旋转涉及i，j，k三个轴的变化，他们是联动的，
当你从i轴向j轴转动时，k轴向ij向量积的方向转动

你可能会问一个轴怎么转动向他所指的方向转动？
事实上这个轴是投影在三维空间的一个半径为无穷大的圆...

在这里有一个3Blue1Brown的交互性视频，如果你无法理解我的概念可以自己去试着操作一下超球（Hypersphere）
https://eater.net/quaternions/video/quatmult

看，这是旋转之前的投影

现在我们绕k轴旋转
$q_1=0.8+0.0i+0.0j+0.6k$
$q_2=1$
即
$q_{1}p\ast 1$
$q_1$模长1，确保四维超球不会变形
我们看

可以看到确实旋转了，我们来看看k轴的情况


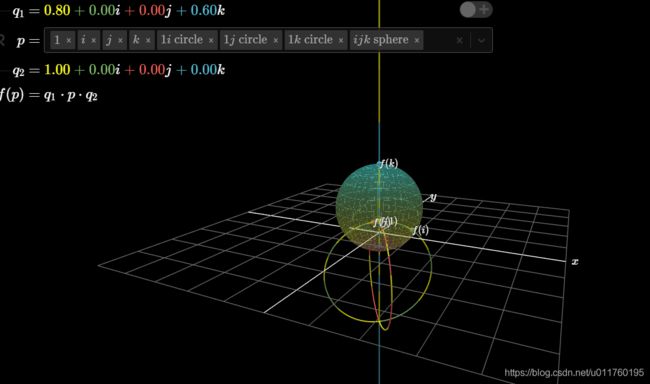
球体变形了，他膨胀了！

为什么？我们明明限制了$q_1$的模长1
根据运算结果，w不为0时偏离了我们的三维空间，导致超球在三维的投影变形了

如何去修复他？
我们左乘一个$q_2$，使得其按左手法则，向相反的方向旋转k轴，将超球拉回w=0处
当然，为了不变形超球，$q_2$模长 = 1，
我们做稍稍调整，$q_2=(w,-q_1.x,-q_1.y,-q_1.z)$
并用$q_2$左乘p，这样便可以抵消w的偏移

你可以同时拿出你的右手和左手，让食指从i轴的方向旋至j轴的方向，一个对应q1，另一个对应q2
两根拇指的方向相反，但是食指的转动的方向相同

也就是说：为了调整偏离w = 0的操作我们旋过了两倍$q_1$的操作。
或者说，要旋转$(\alpha ,\beta ,\gamma )$欧拉角，我们应该使q1等于其一半
$q_1=euler(\frac{\alpha }{2}，\frac{\beta }{2}，\frac{\gamma }{2})$
之后$q_{1}p{q}_2$ 即可

至此，四元数的三维空间旋转应用已经结束，下面给出C++代码

C++代码

quaternion.h

// 四元数
// Ayww
// 2018年12月30日15:10:11

#ifndef _QUATERNION_
#define _QUATERNION_
#define _USE_MATH_DEFINES
#include 
#include 
#include 

class quaternion {
public:
#ifdef QUATERNION_DOUBLE
	using _Myvt = double;
#else
	using _Myvt = float;
#endif
	using vec3 = std::tuple<_Myvt, _Myvt, _Myvt>;
	_Myvt w;
	_Myvt x;
	_Myvt y;
	_Myvt z;
	
public:
	explicit quaternion(_Myvt a = 0, _Myvt b = 0, _Myvt c = 0, _Myvt d = 0) :w(a), x(b), y(c), z(d) {}
	~quaternion(){}

	quaternion::quaternion(const quaternion &r) : w(r.w), x(r.x), y(r.y), z(r.z) {}
	quaternion::quaternion(quaternion &&r) : w(r.w), x(r.x), y(r.y), z(r.z) {}
	quaternion& operator=(quaternion const&);
	quaternion& operator=(quaternion &&);

	quaternion operator*(quaternion const &r);
	quaternion operator+(quaternion const &r);

	// 求模的平方
	_Myvt norm_square(void);

	// 求模
	auto norm(void)->decltype(sqrt(w));

	// 共轭
	quaternion conjugate(void);

	// 逆
	quaternion inv(void);

	// 加
	quaternion& add(quaternion const& qr);

	// 右乘
	quaternion& multi(quaternion const& qr);

	// 到欧拉角
	vec3 to_euler(void);

	// 欧拉角转换到四元数
	quaternion& from_euler(_Myvt, _Myvt, _Myvt);

	// 到三维向量
	vec3 to_vector3(void);

	// 三维向量扩充到四元数
	quaternion& from_vector3(_Myvt, _Myvt, _Myvt);
};


quaternion operator*(quaternion::_Myvt const& l,quaternion const &r);
quaternion operator*(quaternion const &l, quaternion::_Myvt const& r);

#endif // !_QUATERNION_

quaternion.cpp

#include "quaternion.h"

quaternion operator*(quaternion::_Myvt const& l, quaternion const &r) {
	return quaternion(l*r.w, l*r.x, l*r.y, l*r.z);
}
quaternion operator*(quaternion const &r, quaternion::_Myvt const& l) {
	return quaternion(l*r.w, l*r.x, l*r.y, l*r.z);
}

quaternion& quaternion::operator=(quaternion const& r) {
	w = r.w;
	x = r.x;
	y = r.y;
	z = r.z;
	return *this;
}
quaternion& quaternion::operator=(quaternion && r) {
	w = r.w;
	x = r.x;
	y = r.y;
	z = r.z;
	r.w = 0;
	r.x = 0;
	r.y = 0;
	r.z = 0;
	return *this;
}

quaternion::_Myvt quaternion::norm_square() {
	return w*w + x*x + y*y + z*z;
}

quaternion::vec3 quaternion::to_vector3() {
	return vec3(x, y, z);
}

quaternion& quaternion::from_vector3(_Myvt v1, _Myvt v2, _Myvt v3) {
	w = 0;
	x = v1;
	y = v2;
	z = v3;
	return *this;
}

// Z - Y - X Euler angles
// https://www.cnblogs.com/21207-iHome/p/6894128.html
std::tuple<quaternion::_Myvt, quaternion::_Myvt, quaternion::_Myvt> quaternion::to_euler() {
	_Myvt a, b, c;

	const _Myvt _eps = 0.0009765625f;
	const _Myvt _thres = 0.5f - _eps;

	_Myvt _test = w*y - x*z;

	if (_test < -_thres || _test > _thres) {// 奇异姿态,俯仰角为±90°

		int s = _test < .0 ? -1 : 1;

		c = -2 * s * atan2(x, w); // yaw

		b = s * (3.1415926535 / 2.0); // pitch

		a = 0; // roll

	}
	else {
		a = atan2(2 * (y*z + w*x), w*w - x*x - y*y + z*z);
		b = asin(-2 * (x*z - w*y));
		c = atan2(2 * (x*y + w*z), w*w + x*x - y*y - z*z);
	}
	return std::make_tuple(a, b, c);
}

quaternion& quaternion::from_euler(_Myvt r, _Myvt p, _Myvt y) {
	this->w = cos(r)*cos(p)*cos(y) + sin(r)*sin(p)*sin(y);
	this->x = sin(r)*cos(p)*cos(y) - cos(r)*sin(p)*sin(y);
	this->y = cos(r)*sin(p)*cos(y) + sin(r)*cos(p)*sin(y);
	this->z = cos(r)*cos(p)*sin(y) - sin(r)*sin(p)*cos(y);
	return *this;
}

quaternion quaternion::conjugate() {
	return quaternion(w, -x, -y, -z);
}

quaternion quaternion::inv(void) {
	auto a = 1.0 / (x*x + y*y + z*z + w*w);
	return quaternion(a*w, a*-x, a*-y, a*-z);
}

auto quaternion::norm(void)->decltype(sqrt(w)) {
	return sqrt(x*x + y*y + z*z + w*w);
}

quaternion quaternion::operator*(quaternion const &qr) {
	quaternion q;
	q.w = w*qr.w - x*qr.x - y*qr.y - z*qr.z;
	q.x = w*qr.x + x*qr.w + y*qr.z - z*qr.y;
	q.y = w*qr.y - x*qr.z + y*qr.w + z*qr.x;
	q.z = w*qr.z + x*qr.y - y*qr.x + z*qr.w;
	return q;
}
quaternion quaternion::operator+(quaternion const &r) {
	return quaternion(w+r.w,x+r.x, y + r.y, z + r.z);
}

quaternion& quaternion::add(quaternion const& qr) {
	x += qr.x;
	y += qr.y;
	z += qr.z;
	w += qr.w;
	return *this;
}

quaternion& quaternion::multi(quaternion const& qr) {
	quaternion q;
	q.w = w*qr.w - x*qr.x - y*qr.y - z*qr.z;
	q.x = w*qr.x + x*qr.w + y*qr.z - z*qr.y;
	q.y = w*qr.y - x*qr.z + y*qr.w + z*qr.x;
	q.z = w*qr.z + x*qr.y - y*qr.x + z*qr.w;
	this->x = q.x;
	this->y = q.y;
	this->z = q.z;
	this->w = q.w;
	return *this;
}

测试代码

#include 
using namespace std;
#include "quaternion.h"

int main(int argc, char**argv) {

	quaternion q,v,invq;
	const float pi = 3.1415926535f;
	v.from_vector3(1, 1, 0);		// 定义旋转点为 (1，1，0)
	const float deg_z = pi / 4.f;	// 定义本次旋转为：绕z轴逆时针转动 45°
	q.from_euler(0, 0, deg_z*0.5f);	// 将绕z轴转动22.5的欧拉角，转换为四元数
	invq = q.inv();					// 求出q的逆
	v = q*v*invq;					// 先用q来旋转v，此时 w 轴偏离了0 ，在三维空间的投影变形，我们再用q^-1使其转回w = 0的位置
	auto t = v.to_vector3();
	cout << "旋转后坐标，x = " << get<0>(t) << ", y = " << get<1>(t) << ", z = " << get<2>(t) << endl;

	return 0;
}

结果：
$x=0,y=\sqrt{2}，z=0$