主题:简介课程,渐近概念的大局观,插入排序和归并排序,递归式函数时间分析(递归树方法)
教材:《算法导论》
收获:很感动地看到算法分析那个log(n)是为什么出现了,更深层还要听第二讲,若不是因为要准备SAS,恨不得马上看。
内容:
1 何为算法分析?
计算机程序运行性能和存储空间的理论分析,叫算法分析。也就是关注2点:1 性能,就是程序跑得快不快; 2 存储空间,即占用了多大的内存。但是主要还是关注性能。(可能是因为时间就是金钱吧,而且现在计算机硬件发展速度还不错)
2 比性能更加重要的因素都有哪些?
比如成本,正确性,功能特征(features),用户用好,模块化性等等。
3 那为何还学习算法和性能?
很妙的引入方法,你都说了上面那些东西比性能还重要,那尼玛干嘛还要学习算法?
学习算法的原因:
A performance measures the line between the feasible and the infeasible.
对于很多比性能更重要的因素,其实他们跟性能是密切相关的,比如用户用好,就需要你的程序响应时间控制在一定范围内。算法总是处在解决问题的最前沿。
B algorithms give us a language for talking about program behavior.
算法给出了程序行为的描述。
其实形象的比喻就是:水,食物这些东西都比钱重要,你为什么还需要钱?算法就像经济社会中的“货币”,它给出了衡量的一般标准。比如你付出了性能来追求安全稳健性,用户友好性等等。
比如JAVA程序一直很流行,其实它的性能比起C语言要差3倍多,但是由于它本身的面向对象,异常机制等原因,使得人们还是很愿意牺牲性能来追求可拓展性,安全性这些东东。个人的理解就是,比如在软件设计中,你要着重追求某些方面,那在哪种程度范围内是可以接受的呢?性能就是一个标准,比如牺牲3倍性能可以接受,10倍就不行。
C tons of fun
追求速度总是很有趣的,所以人们才会热衷于赛车,火箭等东西。
4 引入插入排序
插入排序(Insertion Sort)
4.1 描述:
输入 A[1…n],要输出 A’[1,…n],使得A’中的元素按升序排序,也就是a’(1)<=a’(2)<=a’(3)…
4.2 伪代码:
For j=2 to n
{
Do key=a[j]
i=j-1;
While i>0 and a[i]>key
{
Do a[i+1]=a[i]
I=i-1;
}
A[i+1]=key
}
4.3 举例:
1 7 3 6 4 20 13 9
T1:看第二个元素,7,比1大,放在第二位
T2:看第三个元素,3,比7小,把7放到第三位,3再跟1 比较,比1大,所以3放在第二位,结果1 3 7
T3:类似,分析6,结果1 3 6 7
T4..
T7:1 3 4 6 7 9 13 20
4.4 本质:
每次循环后前面已经排好序的部分保持不变(这里的不变应该是指不用管了,而不是位置绝对不变),每次循环的目的是完成增量,使得已经排序的长度+1
5 通过插入排序,看运行时间依赖哪些因素,引入算法分析的渐近分析符号
5.1 运行时间依赖因素
A 输入的数列,如果已经排好序,工作量近似为0,而如果是逆序的,工作量最大
B 输入的数列规模n。6个数VS 6亿个数,所以后续的运行时间分析时,我们把时间看成是n的函数
5.2 T(n)引入
一般我们都想知道运行时间的下届,就是最差的情况,这样子对用户是一个保证,你可以跟人家说这个程序最多不超过3s,但是你不会说最少要3s吧,天知道最好3s,最差要多久,说不定是一辈子。
所以在算法分析中,我们一般是做最坏情况分析,可以用T(n)表示最长的运行时间,
T(n)is the max time on any input size n.
有时候我们也讨论平均情况。此时T(n) is the expected time over all input size n.也就是T(N)表示期望时间。
(什么是期望时间,数学上的公式是每种输入运行时间*每种输入出现的概率,通俗来讲就是加权平均。)
那么每种输入出现的概率是多大呢?我们假设一种统计分布:均匀分布,当然也可以选择其他分布。均匀分布,也就是说,每种输入出现的概率是一样的。
最好情况分析,这个是假象,一般是拿来忽悠人的。没什么用。
运行时间依赖于具体的机器,所以一般分析的时候是考虑相对速度,也就是在同一台机器上的运行速度。(相反的就是绝对速度,也就是在不同机器上做比较)
6 算法的大局观:The Big idea of algorithm——渐近分析
6.1 基本思路是:
忽略掉那些依赖于机器的常量(比如某条具体操作运行时间,如赋值操作),而且,不是去检查实际运行时间,而是关注运行时间的增长。什么意思呢?就是关注的是当输入规模n——》无穷时,T(n)是什么情况,而不是说n=10的时候的详细比较。
6.2 具体
渐近符号:Θ(n)
运算法则:对于一个公式,弃去它的低阶项,并忽略前面的常数因子。比如
Θ(3n^3+90n^2-5n+69)=Θ(n^3)
简单吧!
其实Θ(n)是有严格的数学定义的(下节课再一起讲),所以算法导论这门课既是讲数学,也是讲计算机科学的。
6.3 数学与工程的trade-offs
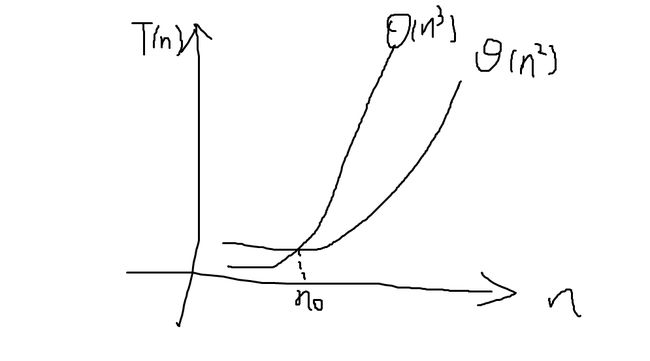
从图中(这个图画得不是一般的丑)可以看出,当n0趋于无穷时,Θ(n2)<<Θ(n3)
有时候交点n0太大,计算机无法运行,所以我们有时会对一些相对低速算法感兴趣。应该就是理论与实际的妥协trade-offs。
7 插入排序运行时间分析
插入排序最坏情况:
T(n)=2+3+…+n=(2+n)(n-1)/2=Θ(n^2)
插入排序算不算快?
对于较小的n,还算是很快的,但是对于大n,它就不算快了,更快的一种排序算法是归并排序。
8 引入归并排序
8.1 归并排序步骤
S1:如果n=1,那么结束;
S2:否则,递归地排序A[1,…[n/2]]和A[[n/2]+1,…n]
S3: 将2个已经排序好的表合并在一起(’Merge’)
8.2 归并子程序
这里用到了一个归并子程序,这也是这个算法的关键。
假设2张已经按照从小到大排序好的表,如何合并?
因为最小的元素一定是2张表中首个元素之一。所以每次对比2张表中最小元素即可。
举例:
1 7 11 13 15 19
3 4 9 18 20 22
首先比较1,3,取1,然后第一个表划掉1
然后比较7和3,取3,然后第二个表划掉3
然后比较7和9,取7,然后第一个表划掉7
以此类推
这个过程运行时间是Θ(n),因为每个元素用了一次对比,是常数时间,然后做了n次,所以是Θ(n),也就是线性时间。
9 归并排序运行时间分析(递归树方法)
所以T(n)={Θ(1) if n=1;
2T(n/2)+Θ(n)(if n>1)(注意:Θ(n)+Θ(1)=Θ(n)}
已经知道递归式子了,那么运行时间如何求解?
可以用递归树的方法求解运行时间,具体的在Lecture2 会讲到,我们只要考虑n>1的情况即可
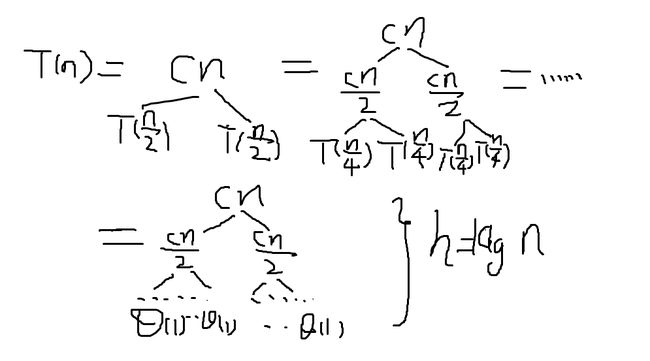
此时T(n)可以表示成为2*T(n/2)+C*n
构造递归树方法:
1 先把递归式子的左半部分写出来
注意:式子右边树上的叶子加起来正好就是T(n),比如第一颗树,T(n)=Cn+T(n/2)*2
高度(层数)约为log(n)(视频上写着log(n),个人觉得应该是表示log2(n),后面也直接用log(n)表示)
这里强调“约”,是因为n不一定是2的整数幂,但是接近。
假设n是2的整数幂,那么讲到Θ(1),正好有log(n)步,n->n/2->n/4->…1,实际上是log(n)的常数倍。
最底层的叶子节点数目是n
T(n)表达式?
为了得到T(n),考虑把所有树上叶子加起来是多少。
除了最后一层,每一层的综合都是C*n,最后一层不一定是C*n,因为边界情况可能存在别的值,记为Θ(n)
所以总数T(n)=Cn*log(n)+Θ(n)(第一项比第二项高)=Θ(n*logn)
考虑渐近情况下,Θ(n*logn)比Θ(n2)要快,所以归并排序在一个充分大的输入规模n下将优于插入排序。
10待解决疑问:
1比如递归树原理,有待下一讲一些理论
2 为什么在渐近情况下,Θ(n*logn)<<Θ(n2)