快速相交检测：平面与包围盒

1.前言

   在游戏等实时性要求高的三维程序中，相交检测是一项及其基础又重要的技术，大佬们相继提出各种检测技术。
  当然大多数人的实现方式可能 （确信）是将包围盒的8个点分别带入平面检测，这将要做8组点积。
  今天我来介绍其中一项比较快速的检测方法，在略去相交和内部的判断后可以直接降到四次点积，当然如果使用的是AABB则会变成一次点积，目前我是按照OBB的方式来算的。

2.数学背景

平面方程形式：$Ax+By+Cz+D=0$
对于坐标$P(x_0,y_0,z_0)$
检验其是否在平面内，可以直接带入平面方程
$A{x}_0+B{y}_0+C{z}_0+D$

• 若结果>0，则在平面外部。
• 若结果=0，则在正好在平面上。
• 若结果<0，则在平面内部。

什么？你问我平面还分内外？
这个我也无法解释，毕竟我只是一只鸽子
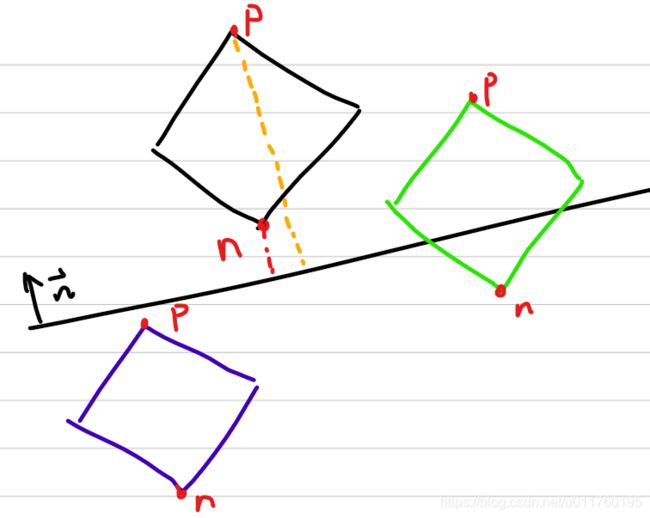
目前我个人来说，习惯性将平面法向量指向的那一侧称呼为外部，法向量负方向一侧称为内部

3.计算原理

   最重要的步骤是找到包围盒的n顶点和p顶点。

• 如果n顶点位于平面外部，则直接返回包围盒在平面外。
• 如果n顶点位于平面内部，p顶点位于平面外部，返回包围盒与平面相交。
• 如果n顶点位于平面内部，p顶点位于平面内部，返回包围盒在平面内。

那么n、p顶点如何寻找呢，通过将平面法向量与包围盒的轴方向进行点积，判断点积结果的正负来寻找。

4.代码

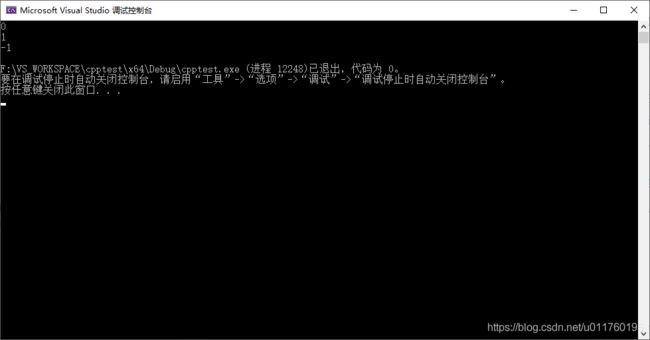
ok，按照惯例先放出结果图

• 0代表在外部
• 1代表相交
• -1代表在内部

测试用例包围盒为在点（0，0，0），长为（1，1，1），第一个轴方向为（1，0，0），第二个轴方向为（0，1，0），第二个轴方向为（0，0，1），对就是xyz轴方向
第一个是在点（2，2，2），法向量为（-1，-1，-1）的平面测试
第二个是在点（0.5，0.5，0.5），法向量为（-1，-1，-1）的平面测试
第三个是在点（-2，-2，-2），法向量为（-1，-1，-1）的平面测试

#include "pch.h"

#include 

using namespace std;

class vec3
{
     
public:
	float x, y, z;
};
class box
{
     
public:
	box(vec3 dx,vec3 dy,vec3 dz,vec3 l,vec3 o)
		:dX(dx),
		dY(dy),
		dZ(dz),
		len(l),
		origin(o)
	{
     

	}
	vec3 dX, dY, dZ;
	vec3 len;
	vec3 origin;

};

float dot(vec3 a, vec3 b)
{
     
	return (a.x * b.x + a.y * b.y + a.z * b.z);
}

class plane
{
     
public:
	plane(vec3 v,vec3 n)
	{
     
		a = n.x;
		b = n.y;
		c = n.z;
		d = -(dot(v,n));
	}

public:
	float check(vec3 x)
	{
     
		return (x.x * a + x.y * b + x.z * c + d);
	}
public:
	union {
     
		struct
		{
     
			float a, b, c;

		};
		vec3 n;
	};
	float d;

	
};

vec3 operator+ (vec3 const& _Left, vec3 const& _Right) noexcept
{
     
	return (vec3{
      _Left.x + _Right.x , _Left.y + _Right.y , _Left.z + _Right.z });
}

vec3 operator* (float _Left, vec3 const& _Right) noexcept
{
     
	return (vec3{
      _Left* _Right.x , _Left* _Right.y , _Left* _Right.z });
}

int check(box _box,plane _plane)
{
     
	auto res1 = dot(_plane.n,_box.dX);
	auto res2 = dot(_plane.n, _box.dY);
	auto res3 = dot(_plane.n, _box.dZ);

	char mask_n = 0 | (res1 >= 0 ? 0 : 1) | (res2 >= 0 ? 0 : 2) | (res3 >= 0 ? 0 : 4);

	vec3 _n = _box.origin;

	if (mask_n & 1)
	{
     
		_n = _n + (_box.len.x * _box.dX);
	}

	if (mask_n & 2)
	{
     
		_n = _n + (_box.len.y * _box.dY);
	}

	if (mask_n & 4)
	{
     
		_n = _n + (_box.len.z * _box.dZ);
	}

	if (_plane.check(_n) < 0.0)
	{
     
		char mask_p = ~mask_n;
		vec3 _p = _box.origin;

		if (mask_p & 1)
		{
     
			_p = _p + (_box.len.x * _box.dX);
		}

		if (mask_p & 2)
		{
     
			_p = _p + (_box.len.y * _box.dY);
		}

		if (mask_p & 4)
		{
     
			_p = _p + (_box.len.z * _box.dZ);
		}

		if (_plane.check(_p) < 0.0)
		{
     
			// inside
			return (-1);
		}
		else
		{
     
			// intersect
			return (1);
		}
	}
	
	// outside;
	return 0;
}

int main()
{
     

	plane p1({
      2,2,2 }, {
      -1,-1,-1 });
	plane p2({
      0.5,0.5,0.5 }, {
      -1,-1,-1 });
	plane p3({
      -2,-2,-2 }, {
      -1,-1,-1 });

	box _box({
     1,0,0},
		{
      0,1,0},
		{
      0,0,1 },
		{
     1,1,1},
		{
     0,0,0});

	std::cout << check(_box, p1) << std::endl;
	std::cout << check(_box, p2) << std::endl;
	std::cout << check(_box, p3) << std::endl;

	return 0;
}