lingo入门——从河北省第三届研究生建模竞赛B题开始
lingo,语法简便、程序较小且使用不受限,对规划问题又有奇效,正是建模人的利器。博主会在这里就河北省第三届研究生建模竞赛B题,贴出对应的lingo程序并做出适当解释。希望能给后来新学者一些启发,便于入门。如果有小伙伴对解析过程有所不理解或者有异议,欢迎在评论区讨论,我会及时回复的!d=====( ̄▽ ̄*)b
鉴于很多小伙伴找我要代码,这里贴一下网盘链接‘
链接:https://pan.baidu.com/s/1a5865l3kgZIryDwzHsT3rA
提取码:p8js
备注1:这里给的代码是包含全部四个题目的
备注2:我给的几个程序要想跑出全局最优解还是很漫长的但是出来局部最优解是很快的,五分钟内结果都是有的。
(有小伙伴反映七个小时都没有出来全局最优解。因为解空间确实过大了,30年15个项目总资金8000万美元,组合太多了。我的模型也只是求解的一个思路,各种约束不够精细又或者算法还有待提高,只能权当抛砖引玉了 /狗头。)
一、题目:投资建模(河北省第三届研究生建模竞赛B题)
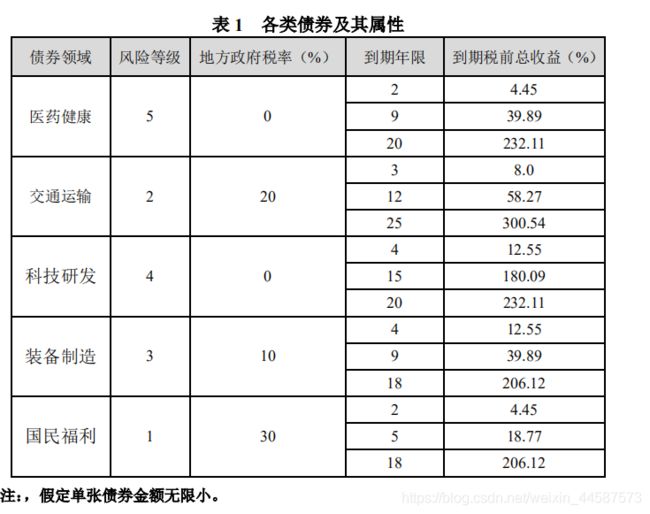
从2021年年初开始到2050年前,未来教育基金会(FFE)向M国部分高等院校捐助一笔经费以帮助贫困学生,将现有的8000万美元资金进行债务投资。
相关投资要求:
(1)医药健康债券购买金额不能少于购买总金额的20%,交通运输、科技研发、装备制造以及国民福利的债券购买金额不能少于购买总金额的10%。
(2)所购买债券的平均风险等级不得低于2.5,等级数字越大,风险越低。
(3)所购买的债券的平均到期年限不超过10年。
(4)要求捐助活动结束后FFE继续保留8000万美元资金。
问题
1.若 SEB 债券投资只允许在第一年初进行,分配8000万美元使收益最大。
2. 假定可以进行重复投资,使得 2050 年末的一次性捐款金额达到最大。
3. FFE 改变捐助方式,计划从 2021 开始,在未来 30 年内每年年初捐助一笔每年金额固定的经费。允许重复投资。使得每年捐助的金额达到最大。
4. FFE 为了帮助疫情防控,决定在每年捐助给高校的金额尽量不低于第 3 问 的金额的前提下,投资尽量向医药健康和科技研发上倾斜。原则上规定:医药健康的投资额,尽量与科技研发相等,尽量是交通运输的 1.2 倍,尽量是装备制造 的 1.5 倍,尽量是国民福利的 2 倍。允许重复投资。
由于该题四个问题并没有本质上的区别,我暂时选取其第三问来进行解释,对于其他问题我会贴出代码。
二、模型
变量解释:
| 变量名 | 解释 |
|---|---|
| x x x | 每年年初捐款金额 |
| m o n e y ( j ) money(j) money(j) | 投资债券 j 的资金数量 |
| m o n e y e a r ( i , j ) moneyear(i,j) moneyear(i,j) | 第 i 年投资债券 j 的资金数量 |
| p r o f i t ( i , j ) profit(i,j) profit(i,j) | 第 i 年投资债券 j ,其到期后的税后本息和 |
| t o t a l m o n e y totalmoney totalmoney | 总投资额 |
| m o n e y s t a r t ( i ) moneystart(i) moneystart(i) | 第 i 年年初可支配的资金数量 |
| m o n e y r e s t ( i ) moneyrest(i) moneyrest(i) | 第 i 年年初没有进行投资的空闲资金数量 |
m a x = x max=x max=x
定义 m o n e y money money,
m o n e y ( i ) = ∑ i = 1 30 m o n e y e a r ( i , j ) money(i)=\sum _{i=1}^{30} moneyear(i,j) money(i)=i=1∑30moneyear(i,j)
定义 p r o f i t profit profit,
p r o f i t ( i , j ) = m o n e y e a r ( i , j ) ∗ [ 1 + s h o u y i l v ( j ) / 100 ∗ t a x ( j ) ] profit(i,j)=moneyear(i,j)*[1+shouyilv(j)/100*tax(j)] profit(i,j)=moneyear(i,j)∗[1+shouyilv(j)/100∗tax(j)]
定义 m o n e y s t a r t moneystart moneystart,
m o n e y s t a r t ( 1 ) = 8000 moneystart(1)=8000 moneystart(1)=8000
m o n e y s t a r t ( i ) = m o n e y r e s t ( i ) + ∑ j = 1 15 m o n e y e a r ( i , j ) , 2 ≤ i ≤ 30 moneystart(i)=moneyrest(i)+\sum _{j=1}^{15}moneyear(i,j), \quad 2\le i\le30 moneystart(i)=moneyrest(i)+j=1∑15moneyear(i,j),2≤i≤30
m o n e y s t a r t ( i ) = m o n e y r e s t ( i − 1 ) + ∑ j = 1 15 p r o f i t ( i i ( i , j ) , j ) moneystart(i)=moneyrest(i-1)+\sum _{j=1}^{15}profit(ii(i,j),j) moneystart(i)=moneyrest(i−1)+j=1∑15profit(ii(i,j),j)
其中 i i ( i , j ) ii(i,j) ii(i,j)满足 i i ( i , j ) = i − y e a r ( j ) & & i i ( i , j ) ≥ 1 ii(i,j)=i-year(j)\&\&ii(i,j)\ge 1 ii(i,j)=i−year(j)&&ii(i,j)≥1 ,
i i ( i , j ) \quad\quad ii(i,j) ii(i,j)表示在第 i -1 年年末到期的债券 j 的购买年份,如果没有的话那么就不加进去,即在这个约束下,该式第二项的求和约束并不一定是15个。
\quad\quad 比如第五年年初,其可支配资金moneystart(5)等于第四年年初未使用的资金moneyrest(4),再加上第四年末到期的各类债券,至于投资期限超过四年的几类债券是不参与计算的,这也是 i i ( i , j ) ≥ 1 ii(i,j)\ge 1 ii(i,j)≥1 的意义所在。
约束1:投资比例限制
t o t a l m o n e y = ∑ j = 1 15 m o n e y ( j ) m o n e y ( 1 ) + m o n e y ( 2 ) + m o n e y ( 3 ) > = t o t a l m o n e y ∗ 0.2 m o n e y ( 4 ) + m o n e y ( 5 ) + m o n e y ( 6 ) > = t o t a l m o n e y ∗ 0.1 m o n e y ( 7 ) + m o n e y ( 8 ) + m o n e y ( 9 ) > = t o t a l m o n e y ∗ 0.1 m o n e y ( 10 ) + m o n e y ( 11 ) + m o n e y ( 12 ) > = t o t a l m o n e y ∗ 0.1 m o n e y ( 13 ) + m o n e y ( 14 ) + m o n e y ( 15 ) > = t o t a l m o n e y ∗ 0.1 totalmoney =\sum _{j=1}^{15}money(j) \\money(1)+money(2)+money(3) >= totalmoney*0.2 \\money(4)+money(5)+money(6) >= totalmoney*0.1 \\money(7)+money(8)+money(9)>=totalmoney*0.1 \\money(10)+money(11)+money(12)>=totalmoney*0.1 \\money(13)+money(14)+money(15)>=totalmoney*0.1 totalmoney=j=1∑15money(j)money(1)+money(2)+money(3)>=totalmoney∗0.2money(4)+money(5)+money(6)>=totalmoney∗0.1money(7)+money(8)+money(9)>=totalmoney∗0.1money(10)+money(11)+money(12)>=totalmoney∗0.1money(13)+money(14)+money(15)>=totalmoney∗0.1
约束2:风险等级
∑ j = 1 15 m o n e y ( j ) r i s k ( j ) ≥ 2.5 ∗ t o t a l m o n e y \sum _{j=1}^{15} money(j) risk(j)\ge 2.5*totalmoney j=1∑15money(j)risk(j)≥2.5∗totalmoney
约束3:平均年限
∑ j = 1 15 m o n e y ( j ) y e a r ( j ) ≤ 10 ∗ t o t a l m o n e y \sum _{j=1}^{15} money(j) year(j) \le 10*totalmoney j=1∑15money(j)year(j)≤10∗totalmoney
约束4:最后一年年初还有8000万美元
m o n e y s t a r t ( 30 ) − x + ∑ j = 1 15 p r o f i t ( 31 − y e a r ( j ) , j ) ) > 8000 moneystart(30)-x+\sum _{j=1}^{15}profit(31-year(j),j))>8000 moneystart(30)−x+j=1∑15profit(31−year(j),j))>8000
三、代码
!model:投资问题3;
sets:
i1/1..30/:moneystart,moneyrest;
!moneyear,每年年初可支配的资金;moneyrest,每年年初剩余的没有投资的资金;
i2/1..15/:risk,year,shouyilv,tax,money;!money表示每一项总共投资的资金总额;
i3(i1,i2):moneyear,profit;
endsets
data:
risk= 5 5 5 2 2 2 4 4 4 3 3 3 1 1 1;
year=2 9 20 3 12 25 4 15 20 4 9 18 2 5 18;
shouyilv=4.45 39.89 232.11 8 58.27 300.54 12.55 180.09 232.11 12.55 39.89 206.12 4.45 18.77 206.12;
tax=0 0 0 0.20 0.20 0.20 0 0 0 0.10 0.10 0.10 0.30 0.30 0.30;
enddata
max=x;!设置x为每年捐赠的资金;
@gin(x);
@for(i3(i,j):@gin(moneyear(i,j)));
!31-x=50-x+1-21+1,例2年期的债券j,money(30,j)=0表示该债券第30年初不能进行投资;
@for(i3(i,j)|i#gt#31-year(j)#and#i#lt#31:moneyear(i,j)=0);
@for( i2(j):money(j)=@sum(i1(i):moneyear(i,j)) );
!第i年投资j债券。等完成后的收益;
@for(i3(i,j):profit(i,j)=moneyear(i,j)*(1+shouyilv(j)/100*(1-tax(j))) );
moneystart(1)=8000;
!资金流出:每年年初可支配资金=每年初实际投资的钱+每年年初没有投资的钱+捐款x;
@for(i1(i):moneystart(i)=@sum(i2(j):moneyear(i,j))+ moneyrest(i)+x) ;
!资金流入:每年年初可支配资金=去年初没有进行投资的钱+去年年末到期的钱;
@for(i1(i)|i#gt#1:moneystart(i)=@sum(i3(ii,ij)|ii#eq#i-year(ij)#and#ii#gt#0:profit(ii,ij)) + moneyrest(i-1) );
!约束1:总投资计划中,各部份占总投资数量的百分比;
totalmoney=@sum(i2(j):money(j));
money(1)+money(2)+money(3)>=totalmoney*0.2;
money(4)+money(5)+money(6)>=totalmoney*0.1;
money(7)+money(8)+money(9)>=totalmoney*0.1;
money(10)+money(11)+money(12)>=totalmoney*0.1;
money(13)+money(14)+money(15)>=totalmoney*0.1;
!约束2:平均投资风险等级;
@sum(i2(i):money(i)*risk(i))>=2.5*totalmoney;
!约束3:投资平均年限设置;
@sum(i2(i):money(i)*year(i))<=totalmoney*10;
!约束4:投资完后2051年仍有8000万美元剩下。;
moneystart(30)-x+@sum(i2(j):profit(31-year(j),j))>8000;
end
四、代码逐行解析
行2-7 :设置集合
行9-14 :赋值
行16:目标函数
行18-44:约束条件
行18:对x取整,对解空间进行限制。同时也呼应题设”单张债券金额无限小“的假设
行19:对moneyear取整,对解空间进行限制。
行20-21:到期时间在2050年末之后的债券投资量为0,对解空间进行限制。不管有没有此约束,最优解都会满足这一条件。但是加上这个约束在没有改变模型的解同时还降低了模型求解复杂度。
行22:定义money中间变量,表示累计对每一债券投资的资金总和,便于后文对约束123的处理。
行23-24:定义profit收益。即第i年投资债券j,到期后得到的本息和。
行26-30:对每年年初的资金流入和流出进行定义,是条件4的捐助金额引出的中间变量。
行32-44:对债券投资的四条硬约束。之前这里对约束二的处理有些问题,在新发的代码里进行了修正,感谢小伙伴们的指正。
五、总结
5.1代码总结
整体看来该规划问题的主要硬约束是33行-45行。
18-21约束,主要是为了降低求解复杂度。
22-31是为33-45硬约束做铺垫,他们的存在主要是为了定义中间变量
5.2涉及下标索引的一类约束条件
lingo在求解规划问题时,比较棘手的一种情况是处理涉及下标索引的一类约束条件。
三种基本方法来解决这个问题。
way1:"|##:"的使用,直接对下标进行约束。代码简洁,最优。
第21行程序:
@for(i3(i,j)|i#gt#31-year(j)#and#i#lt#31:moneyear(i,j)=0);。
投资资金在2050年末一次性捐出,那么最优解肯定满足在2050年后到期的债券不能购买,即对应的moneyear(i,j)=0。如两年期的项目 j 在第29年初还可以投资,但是第30年初就不能投资了。即money(30,j)=0;同理其他债券类似。
way2:广设中间变量,
即对不好处理的问题,通过设置中间变量的方法逐步解决。如本文中对约束4的定义,引入了 p r o f i t profit profit来表示第 i 年 投资 j 债券 到期后的本息和。
way3:傻瓜编程
当然如果不是处理大量数据的话,傻瓜编程也是可以接受的。适合建模时候用,不用过多思考下标逻辑,同时也避免了潜在的模型出错。
如本文的约束1(32-38行),几行傻瓜代码解决了这个问题,避免重新构造集合和引入变量,同样也很简洁。
totalmoney=@sum(i2(j):money(j));
money(1)+money(2)+money(3)>=totalmoney*0.2;
money(4)+money(5)+money(6)>=totalmoney*0.1;
money(7)+money(8)+money(9)>=totalmoney*0.1;
money(10)+money(11)+money(12)>=totalmoney*0.1;
money(13)+money(14)+money(15)>=totalmoney*0.1;
5.3最后
本文主要分析了第三小问,关于其余小问的代码不再做过多阐述,我仅上传附件供大家参考。至于结果分析这里就不多加赘述了。
https://download.csdn.net/download/weixin_44587573/12565249。