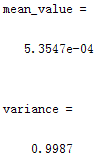MATLAB产生线性扫频信号、高斯白噪声信号、ASK、FSK、PSK、16QAM信号等
文章目录
- 背景:
- 1、高斯白噪声
- 2、噪声调幅信号
- 3、噪声调频信号
- 4、单音信号
- 5、多音信号
- 6、线性扫频信号
- 7、2ASK信号
- 8、2FSK信号
- 9、BPSK信号
- 10、16QAM信号
- 缩略对照表
背景:
临近毕业整理毕业论文的资料时,看到了写论文时仿真的各类常见通信信号,当时每种信号的仿真的都找了挺久的,因为网上有的代码实现太复杂看不太懂,有的代码呈现的效果不太好,所以现在把这些MATLAB代码整理总结一下方便大家直接使用。本文仿真的信号类型有:高斯白噪声、噪声调幅信号、噪声调频信号、单音信号、多音信号、扫频信号、2ASK信号、2FSK信号、BPSK信号、16QAM信号。仿真时主要针对时域波形和频谱进行展示,并对当时的代码加注释方便大家理解。
1、高斯白噪声
在分析通信系统的抗噪声性能时,因为通信系统中常见的热噪声近似为白噪声,且热噪声的取值恰好服从高斯分布,
所以常用高斯白噪声作为通信信道中的噪声模型。其中噪声的统计均值为 0,统计方差为1,并且高斯白噪声的幅值-频次统计直方图服从正态分布。仿真结果如图所示,图1是高斯白噪声的时域波形,图2是高斯白噪声的归一化功率,图3是高斯白噪声的统计信息和幅值用来验证高斯白噪声分布的特点,其中程序的最后两行分别计算了噪声的均值和方差验证是否均值=0,方差=1,本次仿真的均值=5.3547e-4,接近于0,方差=0.9987,接近于1。
length = 1000000;
ff = 0:length-1;
noise = wgn(length,1,0);%生成100000*1个高斯白噪声,功率为0dBW(分贝瓦)
y1 = fft(noise,length);%采样点个数100000个
p1 = y1.*conj(y1);%conj()得到相应的复共轭数,y1.*conj(y1)就是模的平方
max_P=max(p1);%求功率的最大值
p1 =p1/(max_P);%除以最大值把功率谱归一化
subplot(2,2,1),plot(ff,noise(1:length)),axis([0 (length) -5 5]),xlabel('时间(s)'),ylabel('幅值(V)'),title('高斯白噪声波形');
subplot(2,2,2),plot(ff,p1(1:length)),axis([0 length 0 1]);xlabel('频率(Hz)');ylabel('功率');title('高斯白噪声归一化功率谱');
set(gca,'YTick',0:1:1);%设置逻辑值坐标轴为0和1,这样子就不会出现0-0.1-0.2^0.8-0.9-1的坐标,影响美观
subplot(2,2,3),hist(noise,40);axis([ -5 5 0 110000]);xlabel('幅值(V)');ylabel('频次');title('幅值-频次直方图');
mean_value = mean(noise)%计算噪声的均值,理论上应该是0
variance = var(noise)%计算噪声的方差,理论上应该为1,功率为0dBW(10*log1=0)
2、噪声调幅信号
噪声调幅信号是是利用噪声作为调制信号,对载波信号进行AM调制,使得载波信号的振幅随基带噪声做随机变化,这里的噪声使用了上面的高斯白噪声进行调制。其中这里的上包络和下包络只是噪声信号的变形,不是噪声调幅信号真正的包络,只是为了便于理解调幅信号的本质所构造的辅助曲线。
噪声调幅信号的公式为: J ( t ) = ( U 0 + U n ( t ) ) cos ( w j t + φ ) , J(t)=\left(U_{0}+U_{n}(t)\right) \cos \left(w_{j} t+\varphi\right), J(t)=(U0+Un(t))cos(wjt+φ),其中, U 0 U_{0} U0是载波振幅, w j w_{j} wj是载波角频率, U n ( t ) U_{n}(t) Un(t)是基带噪声, φ φ φ在[0,2π]内均匀分布。
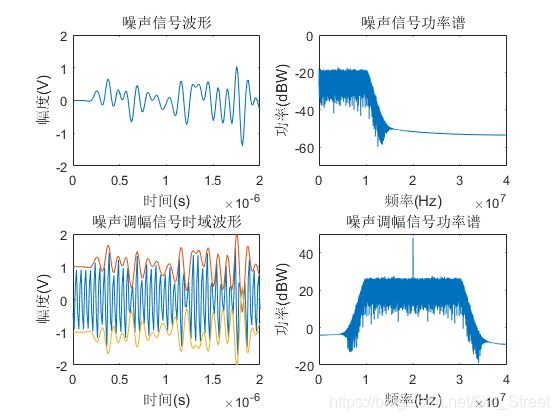
通过分析图中噪声信号和噪声调幅干扰信号的波形与功率谱,可以发现噪声调幅干扰信号具有以下特点:
1) 噪声调幅干扰信号的功率谱由载波谱和对称旁瓣谱构成,旁瓣谱的形状与基带噪声功率谱的形状相似。
2) 噪声调幅干扰信号的带宽为基带噪声带宽的两倍。
fj=20e6;fs=4*fj; Tr=520e-6;
t1=0:1/fs:3*Tr-1/fs; N=length(t1);
u=wgn(1,N,0);%生成N*1个高斯白噪声,功率为0dBW(分贝瓦)
df1=fs/N;n=0:N/2;f=n*df1;
wp=10e6;ws=14e6;rp=1; rs=60;
[n1,wn1]=buttord(wp/(fs/2),ws/(fs/2),rp,rs);
[b,a]=butter(n1,wn1);
u1=filter(b,a,u);
p=0.1503*mean((u1.^2));
figure;subplot(2,2,1),plot(t1,u1),title('噪声信号波形'); axis([0,0.02e-4,-2,2]);xlabel('时间(s)');ylabel('幅度(V)');
subplot(2,2,2), j2=fft(u1);plot(f,10*log10(abs(j2(n+1)*2/N)));xlabel('频率(Hz)');ylabel('功率(dBW)');axis([0,4e7,-70,0]);title( '噪声信号功率谱');
u0=1;y=(u1+u0).*cos(2*pi*fj*t1+2);%噪声调幅信号的波形
u2=u1+u0;%上包络的波形
u3=-u0-u1;%下包络的波形
subplot(2,2,3), plot(t1,y,t1,u2,t1,u3),title( '噪声调幅信号时域波形'); axis([0,0.02e-4,-2,2]);xlabel('时间(s)');ylabel('幅度(V)');
subplot(2,2,4), J=fft(y);plot(f,10*log10(abs(J(n+1))));xlabel('频率(Hz)');ylabel('功率(dBW)');axis([0,4e7,-20,50]);title( '噪声调幅信号功率谱');
3、噪声调频信号
噪声调频信号是是利用噪声作为调制信号,对载波信号进行FM调制,使得载波信号的频率随基带噪声做随机变化,这里的噪声同样使用了上面的高斯白噪声进行调制。
噪声调频信号的公式为: J ( t ) = U j cos ( w j t + 2 π K F M ∫ 0 t U n ( t ′ ) d t ′ + φ ) J(t)=U_{j} \cos \left(w_{j} t+2 \pi K_{FM} \int_{0}^{t} U_{n}\left(t^{\prime}\right) d t^{\prime}+\varphi\right) J(t)=Ujcos(wjt+2πKFM∫0tUn(t′)dt′+φ)其中, U 0 U_{0} U0是载波振幅, w j w_{j} wj是载波角频率, U n ( t ) U_{n}(t) Un(t)是基带噪声, φ φ φ在[0,2π]内均匀分布, K F M K_{FM} KFM是调频斜率,噪声调频信号的幅值是一个常数。
uj=1;mf=2;wpp=10;
fj=20e6;fs=8*fj;Tr=520e-6;
t1=0:1/fs:3*Tr-1/fs;N=length(t1);
u=wgn(1,N,0);
wp=10e6;ws=16e6;rp=1;rs=60;
[n1,wn1]=buttord(wp/(fs/2),ws/(fs/2),rp,rs);
[b,a]=butter(n1,wn1);
u1=filter(b,a,u);
p=0.8503*mean((u1.^2)) ;
fj=20e6;fs=8*fj;Tr=520e-6;bj=5e6;
t1=0:1/fs:3*Tr-1/fs;N=length(t1);
u=wgn(1,N,wpp);
df1=fs/N;n=0:N/2;f=n*df1;
wp=10e6;ws=14e6;rp=1;rs=60;
[Nn,wn]=buttord(wp/(30e6/2),ws/(30e6/2),rp,rs);
[b,a]=butter(Nn,wn);
figure;subplot(2,2,1),plot(t1,u1),title('噪声信号波形');axis([0,2e-6,-2,2]);xlabel('时间(s)');ylabel('幅度(V)');
subplot(2,2,2),j2=fft(u1); plot(f,10*log10(abs(j2(n+1)*2/N)));xlabel('频率(Hz)');ylabel('功率(dBW)');axis([0,4e7,-20,50]);title( '噪声信号功率谱');axis([0,4e7,-80,0]);
i=1:N-1;ss=cumsum([0 u1(i)])
ss=ss*Tr/N;
y=uj*cos(2*pi*fj*t1+2*pi*mf*bj*ss*10);%uj=1 是输出的噪声调频信号的幅度 fj是调制信号中心频率是20M 增加调制指数*10 让波形明显
subplot(2,2,3), plot(t1,y),title( '噪声调频信号波形'),axis([0,2e-6,-1.5,1.5]);xlabel('时间(s)');ylabel('幅度(V)');
y=uj*cos(2*pi*fj*t1+2*pi*mf*bj*ss);%uj=1 是输出的噪声调频信号的幅度 fj是调制信号中心频率是20M
subplot(2,2,4),J=fft(y);plot(f,10*log10(abs(J(n+1))));axis([0,4e7,-20,60]);xlabel('频率(Hz)');ylabel('功率(dBW)');axis([0,4e7,-20,50]);title( '噪声调频信号功率谱')
4、单音信号
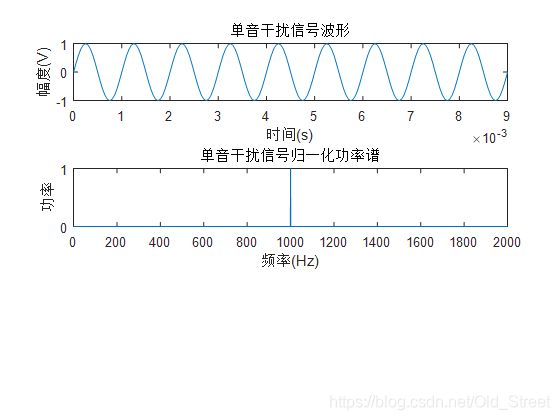
单音信号是一个频率的正弦波。通过MATLAB仿真的是频率为1000Hz、幅值为1V的单音信号。
单音信号的公式为: J ( t ) = U j sin ( 2 π f j t + φ ) J(t)=U_{j} \sin \left(2 \pi f_{j} t+\varphi\right) J(t)=Ujsin(2πfjt+φ)其中, U j U_{j} Uj是单音振幅, f j f_{j} fj是单音频率, φ φ φ在[0,2π]内均匀分布,单音信号只有一根谱线。
Fs=20000; %采样频率
N=20000; %采样点
n=0:N-1;t=n/Fs; %时间序列
fc=1000; %载波信号频率
f=n*Fs/N; %频率
Uc=1*sin(2*fc*pi*t); %载波信号
C1=fft(Uc); %对载波信号进行傅里叶变换
cxf=abs(C1); %进行傅里叶变换
cxf=cxf/max(cxf);%归一化
subplot(3,1,1);plot(t,Uc);title('载波信号波形');xlabel('时间(s)');ylabel('幅度(V)');title('单音干扰信号波形');axis([0 0.009 -1 1]);
subplot(3,1,2); plot(f(1:N/2),cxf(1:N/2));title('载波信号频谱'); axis([0 2000 0 1]);xlabel('频率(Hz)');ylabel('功率');title('单音干扰信号归一化功率谱');
set(gca,'YTick',0:1:1);%设置功率谱坐标轴只有0和1
5、多音信号
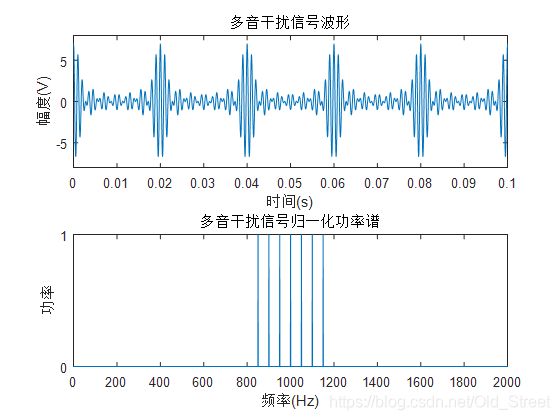
多音信号是由L个独立的正弦信号波形叠加而产生的。通过MATLAB仿真的是940Hz、960Hz、980Hz、1000Hz、1020Hz、1040Hz、1060Hz的多音信号,L=7。
多音信号的公式为: J ( t ) = ∑ n = 1 L U j n sin ( w n t + φ n ) J(t)=\sum_{n=1}^{L} U_{j n} \sin \left(w_{n} t+\varphi_{n}\right) J(t)=∑n=1LUjnsin(wnt+φn),其中 w n = 2 π ( f j + n Δ f ) w_{n}=2 \pi\left(f_{j}+n \Delta f\right) wn=2π(fj+nΔf), f j f_{j} fj是多音起始频率, Δ f \Delta f Δf是多音间隔频率,第n和正弦信号的频率为 f j + n Δ f f_{j}+n \Delta f fj+nΔf,多音信号有*L*根谱线。
Fs=200000; %采样频率
N=200000; %采样点
n=0:N-1;t=n/Fs; %时间序列
A0=1; %信号振幅
fc=1000; %信号中间频率
f=n*Fs/N; %信号步进频率
w0=2*fc*pi;
step=2*pi*50;
Uc=A0*cos(w0*t)+A0*cos((w0+step)*t)++A0*cos((w0+2*step)*t)++A0*cos((w0+3*step)*t)+A0*cos((w0-step)*t)++A0*cos((w0-2*step)*t)++A0*cos((w0-3*step)*t);%多音信号
C1=fft(Uc); %对信号进行傅里叶变换
cxf=abs(C1); %求绝对值
cxf=cxf/max(cxf);%归一化
subplot(2,1,1);plot(t,Uc);xlabel('时间(s)');ylabel('幅度(V)');title('多音信号波形');axis([0 0.1 -8 8]);
subplot(2,1,2);plot(f(1:N/2),cxf(1:N/2));title('载波信号频谱');axis([0 2000 0 1]);xlabel('频率(Hz)');ylabel('功率');title('多音信号归一化功率谱');
set(gca,'YTick',0:1:1);%设置功率谱坐标轴只有0和1
6、线性扫频信号
线性扫频信号的频率时间关系是线性的。通过MATLAB仿真的是起始截止频率为5Hz,扫频斜率为95Hz/s的线性扫频信号。可以参考博客:[线性扫频信号(多周期)]。(https://blog.csdn.net/Old_Street/article/details/105523053)
线性扫频信号的公式为: u ( t ) = Arect ( t T ) cos ( 2 π ( f 0 t + 1 2 μ t 2 ) ) u(t)=\operatorname{Arect}\left(\frac{t}{T}\right) \cos \left(2 \pi\left(f_{0} t+\frac{1}{2} \mu t^{2}\right)\right) u(t)=Arect(Tt)cos(2π(f0t+21μt2)),线性扫频信号的瞬时频率为 f ( t ) = f 0 + μ t ( μ = f 1 − f 0 T ) f(t)=f_{0}+\mu t\left(\mu=\frac{f_{1}-f_{0}}{T}\right) f(t)=f0+μt(μ=Tf1−f0);其中, f 0 f_{0} f0是起始频率, f 1 f_{1} f1是终止频率, μ \mu μ是扫频斜率。
t=0:0.00001:3-0.00001;%3对应3个周期,0.00001为精度
f0=5;%扫频起始频率
fe=100;%扫频截止频率
x=chirp(mod(t,1),f0,1,fe);%1代表的是单周期时间
subplot(3,1,1);plot(t,x);title('三个周期的线性扫频信号波形');xlabel('时间(s)');ylabel('幅度(V)');
ft=f0+(fe-f0)*mod(t,1);
subplot(3,1,2);plot(t,ft);title('线性扫频信号频率-时间图');xlabel('时间(s)');ylabel('频率(Hz)');
t=0:0.00001:1-0.00001;%求频谱时不能对多周期的求,对1个周期进行FFT
x=chirp(t,f0,1,fe);
C1=fft(x); %对载波信号进行傅里叶变换
cxf=abs(C1); %求绝对值
cxf=cxf/max(cxf);%归一化
subplot(3,1,3);plot(cxf); axis([0 150 0 1]);title('线性扫频信号归一化频谱');xlabel('频率(Hz)');ylabel('功率');
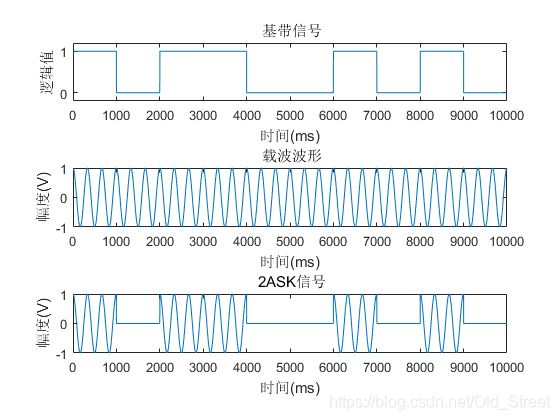
7、2ASK信号
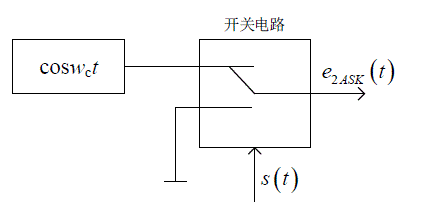
ASK是利用载波的幅度变化来传递数字信息的一种数字调制技术,根据幅度种类的不同,ASK包括2ASK、4ASK、8ASK等。当数字基带信号只取“1”或“0”时,又称为2ASK。2ASK信号的产生比较简单,可以使用通断键控法产生2ASK调制信号。通断键控法的调制原理框图如图所示,通过开关电路实现键控,可以产生2ASK调制信号,当开关通路的时候,输出载波,当开关断路的时候,输出0。当基带信号是1时,2ASK信号与载波信号波形一致,当基带信号是0时,2ASK信号输出0。
2ASK信号的公式为: e 2 A S K ( t ) = { cos w c t 出现概率为P 0 出现概率为1 − P e_{2 ASK\mathrm{}}(t)=\left\{\begin{array}{ll}\cos w_{c} t & \text { 出现概率为P } \\0 & \text { 出现概率为1}-\mathrm{P}\end{array}\right. e2ASK(t)={ coswct0 出现概率为P 出现概率为1−P;其中, P P P是为开关通路的概率对应基带信息中1出现的概率。
N=10;%仿真10S的时间
xn=[];
x=[1 0 1 1 0 0 1 0 1 0];%每秒一个逻辑值,一共10个
t=0.001:0.001:N;%以1ms为步进
for i=1:N
if x(i)==1
xn(i*1000-999:i*1000)=ones(1,1000);
else
xn(i*1000-999:i*1000)=zeros(1,1000);
end
end
y=cos(2*pi*3*t);%载波波形 频率为3Hz
z=xn.*y;%载波调制
subplot(3,1,1);plot(xn);title(' 基带信号');xlabel('时间(ms)');ylabel('逻辑值');axis([0 10000 -0.2 1.2]);
set(gca,'YTick',-1:1:1);%设置逻辑值坐标轴只有0和1
subplot(3,1,2);plot(y);title(' 载波波形');xlabel('时间(ms)');ylabel('幅度(V)');axis([0 10000 -1 1]);
subplot(3,1,3);plot(z);title(' 2ASK信号');xlabel('时间(ms)');ylabel('幅度(V)');axis([0 10000 -1 1]);
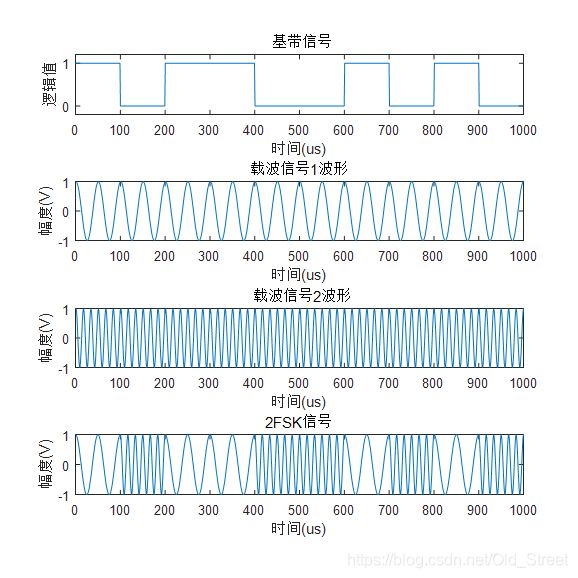
8、2FSK信号
FSK是利用载波的频率变化来传递数字信息的一种数字调制技术,根据频率种类的不同,FSK包括2FSK、4FSK、8FSK等。当数字基带信号只取“1”或“0”时,又称为2FSK。2FSK 可以通过键控法实现,利用受矩形脉冲序列控制的开关电路对两个不同的独立频率源进行选通。当基带信号是1时,2FSK信号与载波信号1波形一致,当基带信号是0时,2FSK信号与载波信号2波形一致。
2FSK信号的公式为: e 2 F S K ( t ) = { A cos ( f 1 t + φ n ) 1 出现概率为P A cos ( f 2 t + θ n ) 0 出现概率为1 − P e_{2 F S K}(t)=\left\{\begin{array}{ll} A \cos \left(f_{1} t+\varphi_{n}\right) & 1 \quad \text { 出现概率为P } \\ A \cos \left(f_{2} t+\theta_{n}\right) & 0 \quad \text { 出现概率为1 }-\mathrm{P} \end{array}\right. e2FSK(t)={ Acos(f1t+φn)Acos(f2t+θn)1 出现概率为P 0 出现概率为1 −P;其中, P P P是为开关通路的概率对应基带信息中1出现的概率。
N=10;%仿真10S的时间
xn=[];xn1=[];
x=[1 0 1 1 0 0 1 0 1 0];%%每秒一个逻辑值,一共10个
t=0.001:0.001:N;%以1ms为步进
for i=1:N
if x(i)==1
xn(i*1000-999:i*1000)=ones(1,1000);%xn都置为0
xn1(i*1000-999:i*1000)=zeros(1,1000);%xn1都置为1
else
xn(i*1000-999:i*1000)=zeros(1,1000);%xn都置为1
xn1(i*1000-999:i*1000)=ones(1,1000);%xn1都置为0
end
end
y=cos(2*pi*2*t);%载波波形1 频率为2Hz
y2=cos(2*pi*6*t);%载波波形2 频率为6Hz
F1=xn.*y; %加入载波1
F2=xn1.*y2; %加入载波2
e_fsk=F1+F2;%叠加
figure(1);heigth=160;width=160;set(gcf,'Position',[0 0 width/0.277 heigth/0.277]);%前面是图片在屏幕的位置,后面是图片大小为20*20
subplot(4,1,1);plot(xn);title(' 基带信号');xlabel('时间(ms)');ylabel('逻辑值');axis([0 10000 -0.2 1.2]);
set(gca,'YTick',-1:1:1);%设置逻辑值坐标轴只有0和1
subplot(4,1,2);plot(y);title(' 载波波形');xlabel('时间(ms)');ylabel('幅度(V)');axis([0 10000 -1 1]);
subplot(4,1,3);plot(y2);title(' 2ASK信号');xlabel('时间(ms)');ylabel('幅度(V)');axis([0 10000 -1 1]);
subplot(414);plot(e_fsk);title('2FSK信号');axis([0 10000 -1 1]);xlabel('时间(ms)');ylabel('幅度(V)');
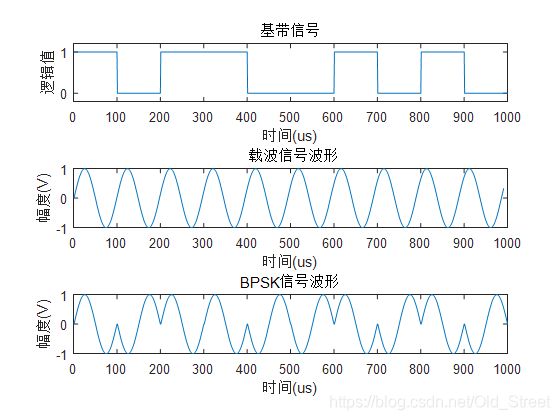
9、BPSK信号
PSK是利用载波的相位变化进行数字信息的传递,根据相位种类的不同,PSK包括BPSK、QPSK、16PSK、64PSK等。以二进制调相为例,取码元为“1”时,调制后载波与未调载波同相;取码元为“0”时,调制后载波与未调载波反相;“1”和“0”时调制后载波相位差π。本章仿真的是BPSK,仅包含0和π两个相位。
PSK信号的通用公式为: s n ( t ) = A cos ( 2 π f 0 t + n 2 π M ) , n = 0 , 2 , … , M − 1 s_{n}(t)=A \cos \left(2 \pi f_{0} t+\frac{n 2 \pi}{M}\right), n=0,2, \ldots, M-1 sn(t)=Acos(2πf0t+Mn2π),n=0,2,…,M−1;其中 M M M代表的是传送信号的符号种类,种类越多,传送的位元数越多,则在固定时间内可以传送的数据量越多,当 M = 2 M=2 M=2时,信号是BPSK信号。
N=10;%仿真10S的时间
xn=[];xn1=[];
x=[1 0 1 1 0 0 1 0 1 0];%每秒一个逻辑值,一共10个
t=0.001:0.001:N;%以1ms为步进
for i=1:N
if x(i)==1
xn(i*1000-999:i*1000)=ones(1,1000);
xn1(i*1000-999:i*1000)=ones(1,1000);%码元值都为1
else
xn(i*1000-999:i*1000)=-ones(1,1000);
xn1(i*1000-999:i*1000)=zeros(1,1000);%码元值都为0
end
end
y=sin(2*pi*1*t);%载波波形 频率为3Hz 与前面的不一样,为正弦波
z=xn.*y;%载波调制
subplot(3,1,1);plot(xn1);title(' 基带信号');xlabel('时间(ms)');ylabel('逻辑值');axis([0 10000 -0.2 1.2]);
set(gca,'YTick',-1:1:1);%设置逻辑值坐标轴只有0和1
subplot(3,1,2);plot(y);title(' 载波波形');xlabel('时间(ms)');ylabel('幅度(V)');axis([0 10000 -1 1]);
subplot(3,1,3);plot(z);title(' 2ASK信号');xlabel('时间(ms)');ylabel('幅度(V)');axis([0 10000 -1 1]);
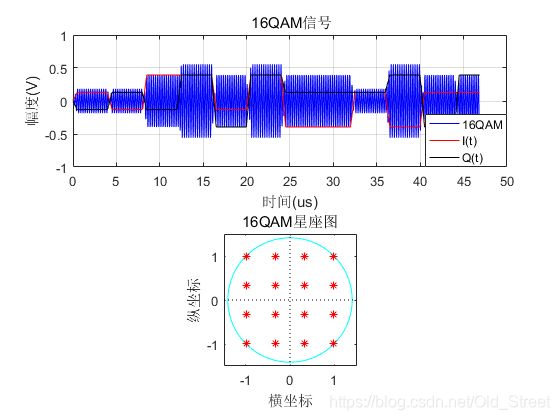
10、16QAM信号
QAM信号是使用QAM调制生成的信号。因为16QAM的程序包含的文件比较多,所以只展示了仿真图。程序放到百度云-链接:https://pan.baidu.com/s/1zxSyYBqJhjAnLdgjqnwOtA
提取码:t8eq,QAM的程序主要来自16QAM百度文库。
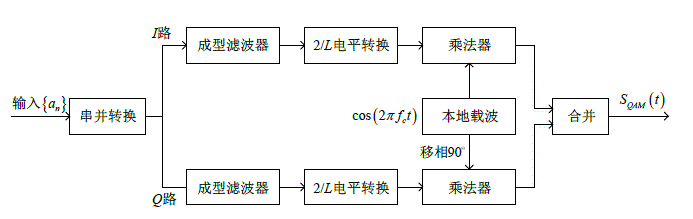
如图是QAM的实现原理,首先将输入二进制bit信号进行串并变换,再分别将两路二进制信号进行2到L的变换产生 I ( t ) I(t) I(t)和 Q ( t ) Q(t) Q(t),接着将两通道的基带信号 I ( t ) I(t) I(t)和 Q ( t ) Q(t) Q(t)分别乘以 cos ( 2 π f c t ) \cos \left(2 \pi f_{c} t\right) cos(2πfct)和 sin ( 2 π f c t ) \sin \left(2 \pi f_{c} t\right) sin(2πfct),最后将两个乘积信号进行矢量和就得到QAM 调制信号。
QAM信号的公式为: S QAM ( t ) = I ( t ) cos ( 2 π f c t ) − Q ( t ) sin ( 2 π f c t ) S_{\text {QAM }}(t)=I(t) \cos \left(2 \pi f_{c} t\right)-Q(t) \sin \left(2 \pi f_{c} t\right) SQAM (t)=I(t)cos(2πfct)−Q(t)sin(2πfct).
缩略对照表
| 2ASK | 2 Amplitude Shift Keying | 二进制幅移键控 |
|---|---|---|
| 2FSK | 2 Frequency Shift Keying | 二进制频移键控 |
| BPSK | Binary Phase Shift Keying | 二进制相移键控 |
| 16QAM | 16 Quadrature Amplitude Modulation | 十六进制正交振幅调制 |
| AM | Amplitude Modulation | 振幅调制 |
| FM | Frequency Modulation | 频率调制 |