自适应波束形成(三)——频域宽带LCMV波束形成器
为了将窄带波束形成扩展至宽带,可以使用频域LCMV波束形成器。首先将麦克风阵列各阵元接收到的信号进行时延补偿,做DFT变换到频域,然后在频域内划分子频带,在每个子频带内运用窄带LCVM算法,最后将得到的结果做IDFT逆变换回时域。尽管频域LCMV波束形成器会降低收敛速度,但可以减少计算复杂度。
1 算法原理
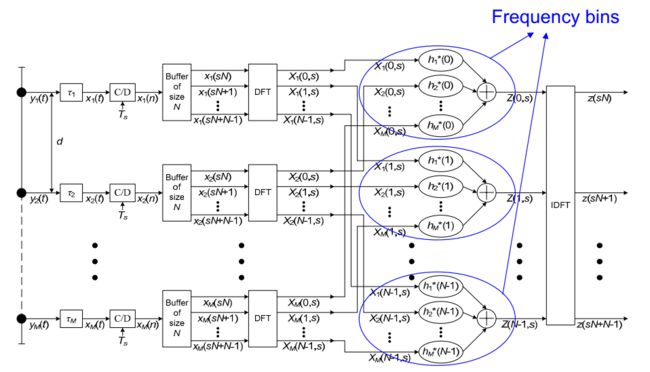
频域LCMV波束形成器的结构如图1所示。
图1 频域LCMV波束形成器
图中yn(t),n=1,2,…,M,为各阵元接收到的信号,进行时延补偿后的到时序一致的信号xn(t),n=1,2,…,M,然后对其采样,得
x(n) = 1Ms(n)+v(n)
其中x(n)=[x1(n) x2(n) …xM(n)]T为采样后信号向量,1M=[1 1 … 1]T,s(n)为期望信号,v(n)= [v1(n) v2(n) …vM(n)]T为噪声向量。将接收到的划分为S段,每段包含N个采样点。考虑第s段,对其做DFT,得到
X(k,s) = [X1(k,s)X2(k,s) …XM(k,s)]T k=0,1,…,N-1
由上两式得
X(k,s) =1MS(k,s) +V(k,s)
其中S(k,s)为我们期望信号,V(k,s) = [V1(k,s) V2(k,s) …VM(k,s)]T。在第s段做N次窄带LCMV波束形成,第k次的输出为
Z(k,s) = wH(k)X(k,s)
其中w(k)=[w1(k) w2(k) …wM(k)]T为滤波器权向量。因此问题转化为求解最优权向量,即
其中RX(k)=E{ X(k,s) XH(k,s)},运用拉格朗日算子,解得
w opt( k) = R X -1( k) 1 M/( 1 M H R X -1( k) 1 M)如果未做时延补偿,则
X(k,s)≅a(θ,k)S(k,s) +V(k,s)≠1MS(k,s)+V(k,s)
其中a(θ,k)=[1 e-jk2πτ2/NTs…e-jk2πτM/NTs]T,τm=(m-1)dsinθ/c,此时解最优权向量方程变为
运用拉格朗日算子,解得
wopt(k) = RX-1(k)a(θ,k)/( aH(θ,k) RX-1(k)a(θ,k))
2 算法仿真
Matlab仿真代码如下:
% 宽带信号频域处理
clear all
clc
% f0 = 1.3*10^9; % 信号中心频率
% fr=1.3*10^9;
% B = 50*10^6; % 信号带宽
f0 = 2.2*10^3; % 信号中心频率
fr=2.2*10^3;
B = 3.6*10^3;
fl = f0-B/2; % 信号起始频率
fh = f0+B/2;
Tr = 50*10^(-6); % 工作周期
T = 10*10^(-6); % 信号持续时间,要求大于孔径渡越时间
% Tr = 5; % 工作周期
% T = 1; % 信号持续时间,要求大于孔径渡越时间
fs = 100*10^6; % 采样频率
snr = [40;0]; % 信噪比
w0 = 40/180*pi; % 指向角
M =8; % 阵元数为M
Kr=1;
Ks = 2; % 信号数目
seta =[0/180*pi,40/180*pi]; % 干扰信号方向
Nm = 6; % 驻留周期个数
Nr = Tr*fs; % 采样点数
N = T*fs;
J = 1000; % FFT的点数
NN = Nm*Nr/J; % 频域快拍数 为么?
c= 340; % 光速
d = 0.5*c/f0; % 阵元间距
x = zeros(M,1); % 数据矢量
R = zeros(M,M); % 接收数据协方差矩阵
tic
% 产生阵列接收的宽带数据
x2 = LFMsource(M,f0,fl,B,fs,T,seta,snr,2); % 期望信号的脉冲宽度为T,出现时间不定
% 产生干扰信号
x1 = LFMsource(M,f0,fl,B,fs,Tr,seta,snr,1);
% u = 1:Nr;
% for k=1:Kr
% for n=1:Nr
% fai(k,n) = rand;
% s(k,n) = exp(i*2*pi*(fr*u(n)/fs+fai(k,n))); % 源信号
% end
% end
% for k=1:Kr
% for m=1:M
% A(m,k)=exp(-i*2*pi*d*fr*(m-1)*sin(seta(k))/c);
% end
% end
% % 阵列接收信号
% x1 = 10.^(snr(1)/20).*A*s;
% 阵列接收的和信号
t1 = 1000; % 任意选择的期望信号出现位置
x1(:,(t1+1):(t1+N)) = x1(:,(t1+1):(t1+N)) + x2;
for nm=1:Nm
x(:,((nm-1)*Nr+1):(nm*Nr)) = x1;
end
noise = randn(M,Nm*Nr)+i*randn(M,Nm*Nr); % 噪声
x = x + noise;
% 时域信号变换为频域信号
fft_8_1;
toc
tic
% 构造方向矢量
w = -90*pi/180:0.01:90*pi/180;
WW = length(w);
P = zeros(1,WW);
Wav=zeros(M,1);
% 计算不同子频点的加权向量
F = fl:B/(J/2-1):fh;
for k = 1:250 %为么是250?
for m = 1:M % 估计子频点对应的协方差矩阵
for n = 1:NN
xf(n,m) = X(k,n,m);
end
end
R = xf.'*conj(xf)./NN;% xf.'??
Ri = inv(R);
for m=1:M
a0(m,1) = exp(-i*2*pi*d*F(k+250)*(m-1)*sin(w0)/c);% 指向向量
end
W = Ri*a0/(a0'*Ri*a0); % 加权向量
for m=1:M
a(m,:) = exp(-i*2*pi*d*F(k+250)*(m-1)*sin(w)/c); % 方向向量,用于方向搜索
end
Wav=Wav+W;
f((k+250),:) = abs(W'*a).^2;
f((k+250),:) =f((k+250),:)./max(f((k+250),:));
end
for k = 1:250
for m = 1:M % 估计子频点对应的协方差矩阵
for n = 1:NN
xf(n,m) = X((k+750),n,m);
end
end
R = xf.'*conj(xf)./NN;
Ri = inv(R);
for m=1:M
a0(m,1) = exp(-i*2*pi*d*F(k)*(m-1)*sin(w0)/c);% 指向向量
end
W = Ri*a0/(a0'*Ri*a0); % 加权向量
for m=1:M
a(m,:) = exp(-i*2*pi*d*F(k)*(m-1)*sin(w)/c); % 方向向量,用于方向搜索
end
Wav=Wav+W;
f(k,:) = abs(W'*a).^2;
f(k,:)=f(k,:)./max(f(k,:));
end
Wav=Wav./500;
for m=1:M
a(m,:) = exp(-i*2*pi*d*f0*(m-1)*sin(w)/c); % 方向向量,用于方向搜索
end
fav=abs(Wav'*a).^2;
fav=fav./max(fav);
f1 = f(1,:)./max(f(1,:));
f2 = f(500,:)./max(f(500,:));
f3 = f(251,:)./max(f(251,:));
% figure;
% plot(w*180/pi,10*log10(f1));
% % title('pattern of linear array(bearing45,interfere20),B=4M,f0=40M,不聚焦,信号不相关(0,40)dB');
% xlabel('\theta/deg');
% ylabel('阵列增益/dB');
% grid on
% legend('最低频率')
% hold on
%
% figure;
% plot(w*180/pi,10*log10(f2));
% xlabel('\theta/deg');
% ylabel('阵列增益/dB');
% grid on
% legend('最高频率')
% hold on
%
% figure;
% plot(w*180/pi,10*log10(f3));
% xlabel('\theta/deg');
% ylabel('阵列增益/dB');
% grid on
% legend('中心频率')
% hold on
%
figure;
plot(w*180/pi,10*log10(f1),w*180/pi,10*log10(f2),w*180/pi,10*log10(f3));
xlabel('\theta/deg');
ylabel('阵列增益/dB');
title('不同频率下波束形成')
grid on
legend('最低频率','最高频率','中心频率')
hold on
%
% figure;
% plot(w*180/pi,10*log10(fav));
% % title('pattern of linear array(bearing45,interfere20),B=4M,f0=40M,不聚焦,信号不相关(0,40)dB');
% xlabel('\theta/deg');
% ylabel('阵列增益/dB');
% grid on
% legend('ISM参考频率')
% hold on
% figure;
% plot(w*180/pi,10*log10(f3),w*180/pi,10*log10(fav));
% xlabel('\theta/deg');
% ylabel('阵列增益/dB');
% grid on
% legend('不做平均的中心频率','平均后的中心频率')
% hold on
figure; % 三维立体图
[XX,Y] = meshgrid(w*180/pi,F);
meshc(XX,Y,10*log10(f/max(max(f))))
title('宽带波束形成');
xlabel('\theta/deg');
ylabel('频率/Hz');
zlabel('阵列增益/dB')
toc
首先产生两个线性调频信号模拟宽带信号,最低频率400Hz,最高频率4000Hz,中心频率2200Hz,正是语音信号的频带范围;信噪比为-40dB,期望信号持续时间为干扰信号的1/5,在干扰信号的1/5处开始加入期望信号。阵元数为16,阵元间距为半波长约为7.7cm,假设期望信号在0o,干扰信号在40o,仿真结果如图2所示。
图2 宽带波束形成增强0o信号
左图是频率为400Hz、2200Hz和4000Hz时对0o信号进行增强的波束图,由图可看出,400Hz时主瓣宽度最大,在40o干扰方向有明显陷波,随着频率的升高主瓣宽度变小,在40o干扰方向上的陷波变得不明显甚至偏差。右图是400Hz~4000Hz的波束图,由图可看出在0o有明显波峰,随频率升高主瓣变窄,说明对高频成分的空间分辨率高于低频成分。
然后改变期望信号和干扰信号的位置,即期望信号在40o,干扰信号在0o,仿真结果如图3所示。
图3 宽带波束形成增强40o信号
由图3能得出相似的结论,右可以看出在0o有较好的陷波。
最后减少一半麦克风阵元数量,即为8个,期望信号在40 o,干扰信号在0 o,仿真结果如图4所示。图4 8个麦克风宽带波束形成
比较图4和图2可知,麦克风阵元数减少一半,主瓣宽度明显变宽,空间分辨率降低,且在0 o的陷波也不明显。说明麦克风阵元数量的减少会降低宽带波束形成的性能。