数字调制：IQ基本理论【转自微信公众号微波射频网】

数字IQ调制凭借高数据速率以及易于实现等优势，广泛应用于无线通信系统。与传统的模拟调制不同，数字调制采用了新颖的IQ调制架构，以0、1比特流为调制信号。简单地讲，数字调制的过程就是将原始数据比特流按照一定的规则映射至IQ坐标系的过程。映射完成后将得到数字I和Q信号，再分别由DAC转换为模拟I和Q信号，最后经IQ调制器上变频至射频频段。

起初接触数字调制的时候，不知道如何理解IQ信号，疑惑比较多。经过长时间的实践和思考，略有心得体会，整理下来供大家参考。因涉及的内容较多，本文主要介绍数字IQ调制的基本理论。

无论是模拟调制，还是数字调制，都是采用调制信号去控制载波信号的三要素：幅度、频率和相位，分别称为调幅、调频和调相。模拟调制称为AM、FM和PM，而数字调制称为ASK、FSK和PSK。数字调制中还有一种调制方式同时包含幅度和相位调制，称为QAM调制(正交幅度调制)。下面将逐一介绍。

1. ASK (Amplitude Shift Keying)

ASK称为幅移键控，只对载波作幅度调制，通常指二进制幅移键控2ASK。2ASK在IQ 坐标系上只有两个星座点，理论上，只要不改变载波相位和频率，星座点的位置可以随意设置。但是为了方便，通常将符号映射至I坐标轴，如图1所示。一个bit可以表征“0” 和“1” 两个状态，状态“0” 对应幅度A1，状态“1” 对应幅度A2。
图1. 2ASK调制映射星座图
类似于模拟AM调制，ASK也具有调制深度的概念，调制深度定义为

当2ASK的调制深度为100%时，只有比特“1”有信号，比特“0”没有信号，所以称为On-Off Keying，简称为OOK调制。OOK是一种特殊的ASK调制，调制后的波形为射频脉冲信号。

图2给出了当调制源为pattern "1001110001101"时，OOK调制之后产生的波形。其中上半图为采用Rectangular filter对应的波形，脉冲波形很完美；下半图为采用Raised Cosine filter时的波形，由于该滤波器具有陡峭的滚降特性，抑制了脉冲信号的高频边带，所以脉冲波形的边沿变得很缓。因此，如果采用OOK方式产生射频脉冲串，一定要采用Rectangular filter。

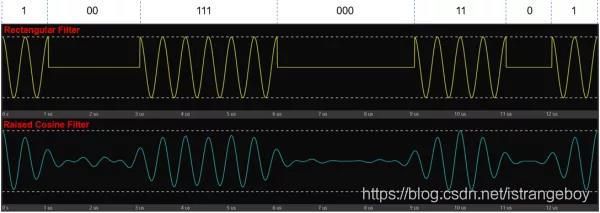
图2. OOK调制生成射频脉冲信号(pattern “1001110001101”

2. FSK (Frequency Shift Keying)

FSK称为频移键控，常见的FSK包括2FSK、4FSK、8FSK、16FSK等。FSK一般不提及星座图，而是将符号映射至频率轴，图3以2FSK和4FSK为例，给出了经典的符号映射关系，纵轴为基带信号频率相对于FSK Peak Deviation的归一化值。

图3. 2FSK和4FSK符号映射方式

FSK是如何实现的呢？以4FSK为例，具有{-1, -1/3, 1/3, 1} 四个归一化频率状态，假设FSK Peak Dev.为3MHz，则四个基带频率分别为{-3MHz, -1MHz, 1MHz, 3MHz }。选择调制源为pattern ‘00011011’，并设置符号速率为1M Sym./s，则在四个频点上都将分别持续1us，即每个符号周期内对应的都是一个CW信号。

虽然FSK并不是将符号直接映射至IQ坐标系中，但是FSK调制依然具有I 分量和Q 分量。因为任何一个频率不为0的基带信号，在IQ坐标系上的矢量轨迹都是一个圆，这意味着在不同时刻，该信号的I 分量和Q 分量也是变化的。

假设基带信号频率为ω1，则用虚指数形式可以表示为，因此在IQ坐标系上，随着时间变化的矢量轨迹为一个圆。根据欧拉公式可得
故I=cos(ω1t)，Q=sin(ω1t) 。

图4. 频率非0时的基带信号矢量轨迹

图5给出了上述例子中4FSK调制的I 和Q 波形，因为符号周期为1us，所以对于f1和f4，一个符号周期内包含三个周期波形。类似地，对于f2和f3，包含一个周期波形。从IQ坐标系的角度看，FSK调制的过程就是沿着轨迹圆作圆周运动的过程，只是基带频率越高，运动速度越快。圆周运动过程中，改变的是载波的相位，因此也可以理解为FSK是通过调相间接实现的。

如果符号速率较高，则符号周期较短，FSK调制过程中很有可能出现一个符号周期只包含部分波形的情况，如图6所示，除了+/-3MHz两个频点是一个完整的周期，+/-1MHz两个频点只有部分波形。

图5. 4FSK调制的IQ波形(1M Sym./s，3MHz deviation)

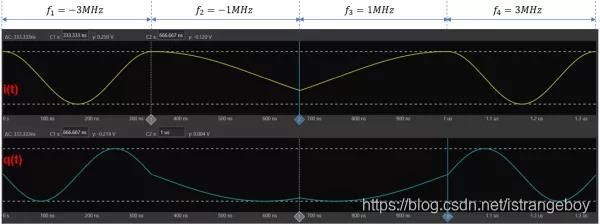
图6. 4FSK调制的IQ波形(3M Sym./s，3MHz deviation)

3. PSK (Phase Shift Keying)

称为相移键控，是非常主流的数字调制方式，常用的PSK包括BPSK、QPSK、OQPSK、8PSK等。PSK调制是将符号直接映射到IQ坐标系上的，图7给出了几组常用的映射方式。

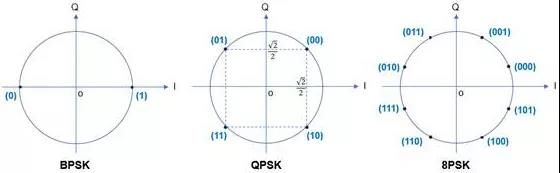
图7. 常见的BPSK/QPSK/8PSK映射方式

下面以QPSK为例，介绍符号映射的过程，其它PSK调制过程与此类似。假设比特流为“00 01 11 10 01 00 11 10 00 11” 共10个符号，按照图7的映射方式，可以得到图8所示的IQ基带波形及其矢量轨迹图。

图中数字1~9表示符号点的跳变轨迹，比如跳频路径1是指从符号(00)跳变至(01)的矢量轨迹，跳频路径2是从符号(01)跳变至(11)的矢量轨迹。其中跳频路径4、6和9会出现I 和Q 同时为0的情况，意味着这一瞬间将没有信号输出。这将导致输出的射频信号具有较高峰均比PAR，如果要求发射平均功率达到某一水平，高PAR对应的峰值功率将更高，对功率放大器的设计提出了挑战。

图8. QPSK调制后得到的基带IQ波形以及矢量轨迹图

为了规避这种过零点“行为”，通过将Q路信号延迟半个符号周期，此时I 和Q 不会同时为0，符号跳变时也就绕开了原点，如下图所示。这种QPSK调制一般称为Offset QPSK，简称为OQPSK；有的文献称为staggered QPSK，简称为SQPSK。

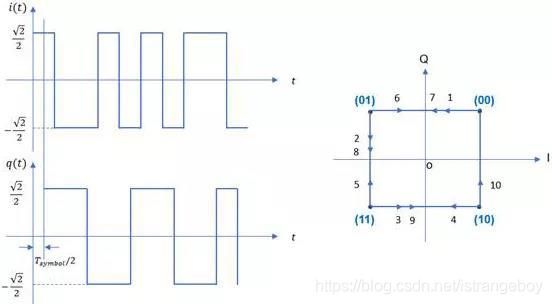
图9. OQPSK调制后得到的基带IQ波形以及矢量轨迹图

4. QAM (Quadrature Amplitude Modulation)

QAM称为正交幅度调制，属于高阶数字调制，一个符号携带多个bit信息，比如16/32/64/128 /256/512/1024 QAM等，在移动通信中较为常用。前面介绍的PSK调制并不会改变载波的振幅，只是改变其相位，而QAM调制相当于调幅和调相结合的调制方式，不仅会改变载波振幅，还会改变其相位。

图10以16QAM调制为例，给出了常用的映射星座图，具有16个星座点，因此一个符号携带4 bits信息。16QAM调制的I 和Q 路信号为4电平信号，作为示例，图11给出了pattern为“0100 0101 0011 1100 0000 0010 1001 1100” 对应的16QAM调制的基带IQ信号波形。

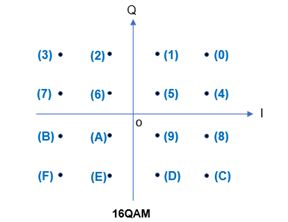
图10. 常用的16QAM映射星座图

图11. 16QAM调制的IQ基带波形(“01000101001111000000001010011100”)

IQ坐标系上映射星座点的I 和Q 决定了载波信号的振幅，而不是包络(有效值)。为了便于证明，下面使用IQ调制的方式产生一个与载波同频的CW信号，对应的I 和Q 分量为一个常数，假设取图12所示的映射点，。经过图13所示的IQ调制器上变频后得到射频信号s(t)为



图12. 选择此映射点用于产生与载波同频的射频信号

可见，射频信号是振幅为1的连续波信号，因此定义了载波信号的振幅。

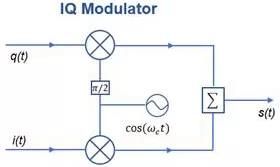
图13. IQ Modulator架构示意图

根据16QAM的星座图可知，任意两个符号之间都有可能存在跳变，而每个符号映射点对应的矢量模值可能不同，相位也可能不同，因此QAM调制会导致载波的振幅发生变化，同时相位也发生变化。

以上简单介绍了常见的几种通用数字调制方式，有时由于系统需要，要求的调制方式比较特殊，这种情况下可以自定义数字调制。自定义数字调制其实就是根据要求自定义星座图，然后按照映射规则实现符号映射，从而完成调制。通常标准测试设备AWG或者VSG都允许用户自定义数字调制，并提供相应的操作界面，图14是Tek一款AWG自定义数字调制的界面，可以直接调整IQ坐标。

图14. 自定义星座点的坐标