相控阵天线matlab程序

clc;
clear all;
%%%%%%当波束指向阵面法向时的天线方向图
%在波束指向阵面法向时的最大增益值,27dB
A=27;
%在波束指向阵面法向时的第一副瓣的增益值,-1dB
B=-1;
%在波束指向阵面法向时的第一零深,-30dB
C=-30;
%在波束指向阵面法向时的半功率点(3dB)宽度(rad)
B_0=1.54*pi/180;
%在波束指向阵面法向时的第一零点(rad)
alpha_1=1.5*pi/180;
%在波束指向阵面法向时的第一旁瓣的峰值所在角度(rad)
alpha_1_5=2.5*pi/180;
%波束指向，方位角rad
alpha_0=60*pi/180;
%波束指向，方位角rad
beta_0=60*pi/180;
%比例系数,01)
%     x22(j)=-x2(k);
%     j=j+1;
%     k=k-1;
% end
% x_2=cat(2,x22,x2);
x_2=[-26.995,-26.3398,-21.1428,-19.6195,-15.1408,-13.0477,-9.0962,-6.5165,-3.0337,0,3.0337,6.5165,9.0962,13.0477,15.1408,19.6195,21.1428,26.3398,26.995];
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%%%%%%%%%%计算 sin(x)=x*C/(0.707*A)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% k=1;
% for i=0:75
% a1=0+i*2*pi;
% b1=pi/2+i*2*pi;
% x1(k)=TwoStep('sin(x)-x*10^(-2.85)/0.707',a1,b1,1,1.0e-4);
% k=k+1;
% a2=pi*0.5959+i*2*pi;
% b2=pi+i*2*pi;
% x1(k)=NewtonDown('sin(x)-x*10^(-2.85)/0.707',a2,b2,1.0e-4);
% k=k+1;
% end
% 
% for i=76:79
% a1=0+i*2*pi;
% b1=pi/2-0.0001*pi+i*2*pi;
% x1(k)=TwoStep('sin(x)-x*10^(-2.85)/0.707',a1,b1,1,1.0e-4);
% k=k+1;
% a2=pi/2+0.00001*pi+i*2*pi;
% b2=pi+i*2*pi;
% x1(k)=NewtonDown('sin(x)-x*10^(-2.85)/0.707',a2,b2,1.0e-4);
% k=k+1;
% end
% j=1;
% k=k-1;
% while (k>1)
%     x11(j)=-x1(k);
%     j=j+1;
%     k=k-1;
% end
% x_1=cat(2,x11,x1);
x_1=[-498.0419,-497.8389,-491.8457,-491.4688,-485.6207,-485.1274,-479.3845,-478.7972,-473.142,-472.4734,-466.8951,-466.1538,-460.6452,-459.8374,-454.3928,-453.5233,-448.1385,-447.2112,-441.8827,-440.9007,-435.6255,-434.5915,-429.3671,-428.2835,-423.1078,-421.9764,-416.8476,-415.6702,-410.5867,-409.3648,-404.325,-403.06,-398.0628,-396.7559,-391.7999,-390.4523,-385.5366,-384.1492,-379.2728,-377.8466,-373.0086,-371.5445,-366.744,-365.2427,-360.479,-358.9413,-354.2137,-352.6402,-347.9481,-346.3394,-341.6822,-340.0389,-335.416,-333.7387,-329.1496,-327.4388,-322.8829,-321.1391,-316.616,-314.8396,-310.3489,-308.5403,-304.0815,-302.2412,-297.814,-295.9423,-291.5463,-289.6436,-285.2785,-283.3451,-279.0104,-277.0467,-272.7423,-270.7485,-266.4739,-264.4504,-260.2055,-258.1525,-253.9369,-251.8547,-247.6682,-245.557,-241.3994,-239.2594,-235.1304,-232.962,-228.8614,-226.6646,-222.5922,-220.3674,-216.323,-214.0702,-210.0536,-207.7732,-203.7842,-201.4762,-197.5147,-195.1793,-191.2451,-188.8825,-184.9754,-182.5858,-178.7057,-176.2891,-172.4359,-169.9925,-166.166,-163.696,-159.8961,-157.3995,-153.6261,-151.1031,-147.356,-144.8068,-141.0859,-138.5105,-134.8158,-132.2142,-128.5456,-125.918,-122.2753,-119.6219,-116.005,-113.3257,-109.7347,-107.0297,-103.4643,-100.7336,-97.1939,-94.4376,-90.9235,-88.1416,-84.6531,-81.8457,-78.3826,-75.5497,-72.1121,-69.2538,-65.8415,-62.958,-59.571,-56.6621,-53.3004,-50.3663,-47.0298,-44.0705,-40.7592,-37.7747,-34.4886,-31.4789,-28.2179,-25.1831,-21.9473,-18.8873,-15.6766,-12.5915,-9.406,-6.2958,-3.1353,0,3.1353,6.2958,9.406,12.5915,15.6766,18.8873,21.9473,25.1831,28.2179,31.4789,34.4886,37.7747,40.7592,44.0705,47.0298,50.3663,53.3004,56.6621,59.571,62.958,65.8415,69.2538,72.1121,75.5497,78.3826,81.8457,84.6531,88.1416,90.9235,94.4376,97.1939,100.7336,103.4643,107.0297,109.7347,113.3257,116.005,119.6219,122.2753,125.918,128.5456,132.2142,134.8158,138.5105,141.0859,144.8068,147.356,151.1031,153.6261,157.3995,159.8961,163.696,166.166,169.9925,172.4359,176.2891,178.7057,182.5858,184.9754,188.8825,191.2451,195.1793,197.5147,201.4762,203.7842,207.7732,210.0536,214.0702,216.323,220.3674,222.5922,226.6646,228.8614,232.962,235.1304,239.2594,241.3994,245.557,247.6682,251.8547,253.9369,258.1525,260.2055,264.4504,266.4739,270.7485,272.7423,277.0467,279.0104,283.3451,285.2785,289.6436,291.5463,295.9423,297.814,302.2412,304.0815,308.5403,310.3489,314.8396,316.616,321.1391,322.8829,327.4388,329.1496,333.7387,335.416,340.0389,341.6822,346.3394,347.9481,352.6402,354.2137,358.9413,360.479,365.2427,366.744,371.5445,373.0086,377.8466,379.2728,384.1492,385.5366,390.4523,391.7999,396.7559,398.0628,403.06,404.325,409.3648,410.5867,415.6702,416.8476,421.9764,423.1078,428.2835,429.3671,434.5915,435.6255,440.9007,441.8827,447.2112,448.1385,453.5233,454.3928,459.8374,460.6452,466.1538,466.8951,472.4734,473.142,478.7972,479.3845,485.1274,485.6207,491.4688,491.8457,497.8389,498.0419];
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
m=1;
n=1;
num=length(-6:0.05:6);
g=zeros(num,num);
for alpha=-6:0.05:6
    alpha_rad=alpha*pi/180;
    for beta=-6:0.05:6
        beta_rad=beta*pi/180;
        delta=acos(cos(alpha_rad)*cos(beta_rad)/(sqrt((cos(alpha_rad))^2+(cos(beta_rad))^2*(sin(alpha_rad))^2)));
        if (delta>=0)&(delta<=B_0/(2*M_0))
            g(m,n)=A*sinc(2*x_0(3)*delta*M_0/B_0)*sqrt(K_0);
            
        elseif (delta>B_0/(2*M_0))&(delta<=alpha_1/M_0)
            g(m,n)=0.707*A*sinc(2*x_1(290)*M_0*(delta-B_0/(2*M_0))/(2*alpha_1-B_0))*sqrt(K_0);
            
        elseif delta>alpha_1/M_0
            g(m,n)=B*sinc(x_2(11)*M_0*(delta-alpha_1_5/M_0)/(alpha_1_5-alpha_1))*sqrt(K_0);            
        else
            disp('输入超界限');
            return;
        end
        n=n+1;
        if n>num
            n=1;
        end
    end
    m=m+1;
    if m>num
        m=1;
    end
end

alpha=-6:0.05:6;
beta=-6:0.05:6;
figure(1)
[alpha,beta]=meshgrid(alpha,beta);
surf(alpha,beta,g)
xlim([-6,6])
ylim([-6,6])

牛顿下山法的实现：

function root=NewtonDown(f,a,b,eps)
%牛顿下山法
%函数名f
%区间左端点a
%区间右端点b
%根的精度eps
%求出的函数零点root

if nargin==3
    eps=1.0e-4;
end

f1=subs(sym(f),findsym(sym(f)),a);
f2=subs(sym(f),findsym(sym(f)),b);
if (f1==0)
    root=a;
end
if (f2==0)
    root=b;
end

if(f1*f2>0)
    disp('两端点函数值乘积大于0！');
    return;
else
    tol=1;
    fun=diff(sym(f));
    fa=subs(sym(f),findsym(sym(f)),a);
    fb=subs(sym(f),findsym(sym(f)),b);
    dfa=subs(sym(fun),findsym(sym(fun)),a);
    dfb=subs(sym(fun),findsym(sym(fun)),b);
    if(dfa>dfb)
        root=a;
    else
        root=b;
    end
    while(tol>eps)
        r1=root;
        fx=subs(sym(f),findsym(sym(f)),r1);
        dfx=subs(sym(fun),findsym(sym(fun)),r1);
        toldf=1;
        alpha=2;
        while toldf>0
            alpha=alpha/2;
            root=r1-alpha*fx/dfx;
            fv=subs(sym(f),findsym(sym(f)),root);
            toldf=abs(fv)-abs(fx);
        end
        tol=abs(root-r1);
    end
end

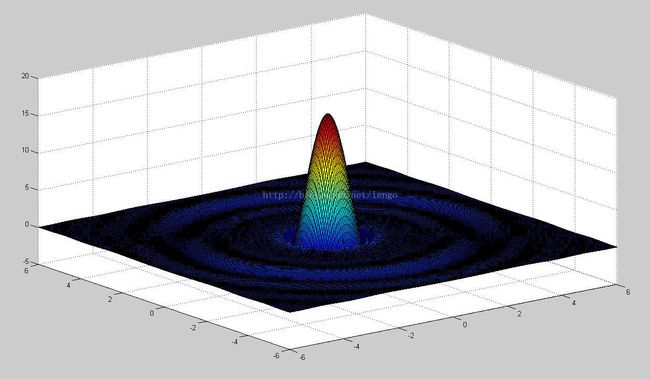
下面是仿真结果：