差分隐私 走过的坑
差分隐私
小记:学了隐私保护相关匿名模型后,初看差分隐私感觉真,一时好难理解,像是个大坑。书上的内容就给一对兄弟数据表,一个ε-差分隐私公式,然后两个实现机制。真的很难结合起来看懂,到底如何差分?如何实现?如何评估?
以下是我初学时一直不理解的几个问题:
- 差分隐私针对怎样的数据进行何样的保护?
- 差分是什么意思?
- 为何给输出结果添加噪声就能使其概率分布近似?
- Laplace机制和指数机制的原理到底什么鬼?
- 隐私保护强度ε、Laplace噪声参数λ、敏感度如何理解?
在知乎上看到一些文章,通俗易懂,各抒己见,可罗列学习。
文章一
作者:Nemo 链接:https://www.zhihu.com/question/47492648/answer/194047182
来源:知乎 著作权归作者所有。
问题提出
2016 年 6 月份,苹果 WWDC 大会上提到了一项 Differential Privacy 差分隐私技术,其作用是能够对用户的数据进行「加密」上传到苹果服务器。苹果能通过这些「加密」过的数据计算出用户群体的行为模式,但是对每个用户个体的数据却无法解析。
从而达到保护个人隐私的目的。
苹果这项技术的实现原理是什么?
- 什么是隐私?
隐私的定义:不同的考量也各抒己见,目前普遍比较接受的是:“单个用户的某一些属性” 可以被看做是隐私。
这个说法里所强调的是:单个用户。也就是说,如果是一群用户的某一些属性,那么可以不看做隐私。
举个例子:医院说,抽烟的人有更高的几率会得肺癌。这个不泄露任何隐私。但是如果医院说,张三因为抽烟,所以有了肺癌。那么这个就是隐私泄露了。好,那么进一步,虽然医院发布的是趋势,说抽烟的人更高几率得肺癌。然后大家都知道张三抽烟,那么是不是张三就会有肺癌呢?那么这算不算隐私泄露呢?结论是不算,因为张三不一定有肺癌,大家只是通过一个趋势猜测的。
因此: 从隐私保护的角度来说,隐私的主体是单个用户,只有牵涉到某个特定用户的才叫隐私泄露,发布群体用户的信息(一般叫聚集信息)不算泄露隐私。
记得高德地图发过一张图,大意是开凯迪拉克的群体喜欢去洗浴中心…很多人说暴露隐私,
其实从学术定义上来说,这个不算隐私泄露,因为没有牵涉到任何个体。
那么我们是不是可以任意发布聚集信息呢?倒是未必。
我们设想这样一种情况: 医院发布了一系列信息,说我们医院这个月有100个病人,其中有10个感染HIV。假如攻击者知道其中99个人是否有HIV的信息,那么他只需要把他知道的99个人的信息和医院发布的100人比对,就可以知道第100个人是否感染HIV。
这种对隐私的攻击行为就是差分攻击。
当然,差分隐私一般针对统计数据库的隐私泄露问题,即用户或攻击者看不到数据库的数据集,他们只能通过对数据库查询获取某些统计数据值。
例如上例,攻击者可查询医院数据库,获取当月患病总人数100,和感染HIV的人数10,并且攻击者已经拥有最大背景知识,知道其中99人的信息。从而进行差分攻击。
- 差分隐私
差分隐私顾名思义就是防止差分攻击了,它想做的事情就是即使你小子知道我发布的100个人的信息,以及另外99个人的信息,你也绝对没办法把这两个信息比对之后获取第100个人的信息。怎么才能做到这一点呢?
差分隐私于是定义:如果你能找出一种方法让攻击者用某种方式查询100个信息和查询那99个信息得到的结果是一致的,那攻击者就没办法找出那第100个人的信息了。
但这个“一致” 怎么做到呢?那就加入随机性吧。
如果查询100个记录和查询99个记录,输出同样值的概率是一样的,攻击者就无法进行差分攻击。
这里我们就得到了差分隐私的核心思想:对于差别只有一条记录的两个数据集,查询它们获得相同值的概率非常非常的接近。
Wait,不是说一致的么?为什么变成了非常接近了? 这是因为,如果概率一样,就表示数据集需要完全随机化,那数据的可用性就没有了,隐私保护也没有意义了。所以,我们尽可能的把概率做的接近,而不是一致,以期在隐私和可用性之间找一个平衡。
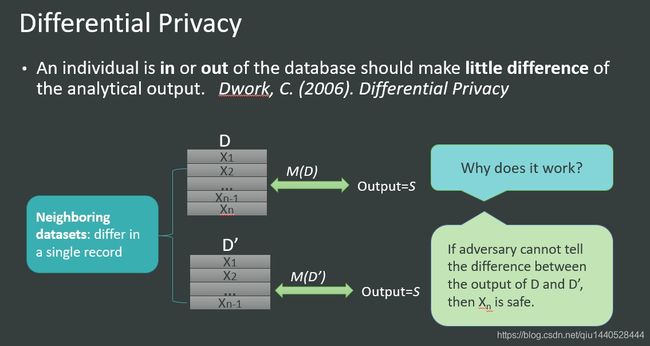
上面这张图描述了差分隐私的基本思想:
对于两个只相差一条记录的数据集D和D’来说,查询M的输出结果S的概率应该非常接近。
Differential Privacy (DP)的严格定义如下:

参数ε 接近0时,exp(ε )接近1,两个概率接近相等,保密程度高。
ε 越大,越没隐私,但查询结果可以更精确。
DP就是为了允许研究者在不泄露个体信息(用户隐私)的前提下,对一个数据集的整体(用户行为)进行分析而研究出的加密手段。
通俗来讲,这个机制保证了一个数据集的每个个体都不被泄露,但数据集整体的统计学信息(比如均值,方差)却可以被外界了解。因此,比如一个医疗机构要公布患者的疾病数据给外界以供研究,就可以先对这个数据集做一个满足DP的扰动,再公布出去。
- 如何做到差分隐私
其实就是在查询结果里 加入随机性。
任何一种方法,只要用在数据集上能满足差分隐私的核心思想,那这个方法就是满足差分隐私的。所以最常用的方法是在结果上加满足某种分布的噪音,使查询结果随机化。
目前常用的有两种方法,一个是Laplace机制,在查询结果里加入Laplace分布的噪音,适用于数值型输出。
例如: zhihu里有多少人是985大学毕业的? 假如结果是2000人,那么加噪后,每一次查询得到的结果都会稍稍有些区别,比如有很高的概率输出2001,也有较高概率输出2010, 较低概率输出1990,等等。
另外一个是指数机制,在查询结果里用指数分布来调整概率,适用于非数值型输出。
例如: 中国top 3大学是哪一所。很高概率输出 浙江大学,较高概率输出上海交大,较低概率输出武汉大学,很低概率输出蓝翔技校,等等。
- 差分隐私应用
这么说吧,任何需要保护隐私的算法里都可以使用差分隐私。
差分隐私最美丽的一点在于只要你的算法每一个步骤都满足差分隐私的要求,那么它可以保证这个算法的最终输出结果满足差分隐私,
换句话说,即使攻击者具有足够多的背景知识,也无法在最终的输出中找出单个人的某项属性。
| 目前在学术上,差分隐私可以被应用在 |
|---|
| 推荐系统 |
| 社交网络 |
| 基于位置的服务 |
| 当然,也包括了苹果的输入系统 |
- 差分隐私的弱点
差分隐私的弱点其实很明显:
- 由于对于背景知识的假设过于强,需要在查询结果中加入大量的随机化,导致数据的可用性急剧下降。
- 特别对于那些复杂的查询,有时候随机化结果几乎掩盖了真实结果。这也是导致目前应用不多的一个原因。
但差分隐私作为一个非常漂亮的数学工具,为隐私研究指明了一个发展的方向。
- 在早期,人们很难证明我的方法保护了隐私,更无法证明究竟保护了多少隐私。
- 现在差分隐私用严格的数学证明告诉人们,只要你按照我的做,我就保证你的隐私不会泄露。
有兴趣可以移步Havard的Differential Privacy实验室,
他们做了一个DP的原型实现,你可以传一个数据集上去,得到一个加密过的新数据集:Differentially Private Curator
更有意思的是,Dwork团队2015年提出应用差分隐私的想法可以解决机器学习的over-fitting问题,一步从隐私界跨到了AI界,开始抢机器学习的饭碗了。她们的论文发表在了2015年的Science上,有志于抢AI饭碗的同学可以瞄一下。
The reusable holdout: Preserving validity in adaptive data analysis
- 最后,放一篇作者朱老师在2017年写的有关差分隐私的前世今生,很学术,有兴趣研究这个方向的同学可以读读。
Differentially Private Data Publishing and Analysis: a Survey
附录一篇Dwork的比较老的综述。
Differential Privacy: A Survey of Results