阵列天线方向图乘积定理的Python实现

简述

我前面的一篇博客已经对方向图乘积定理进行了C#的实现，https://blog.csdn.net/qq_23176133/article/details/85641248，这次用python实现，并为接下来的阵列天线综合做准备。

效果如下

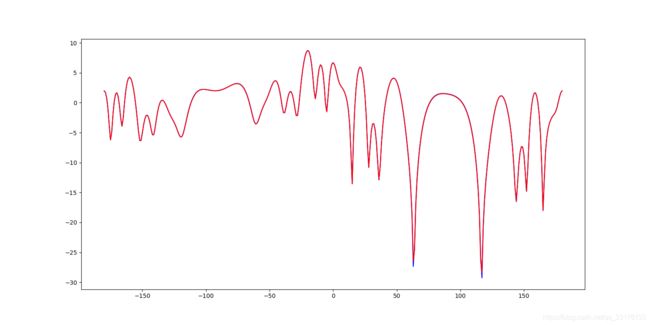
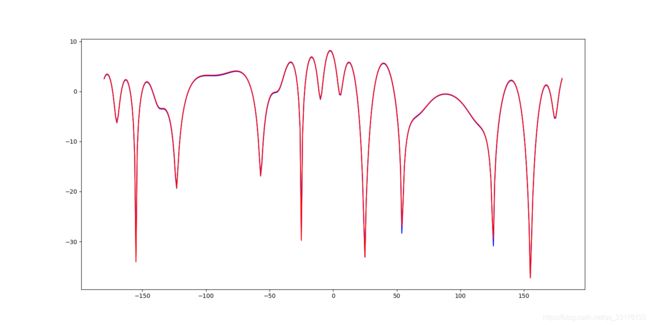
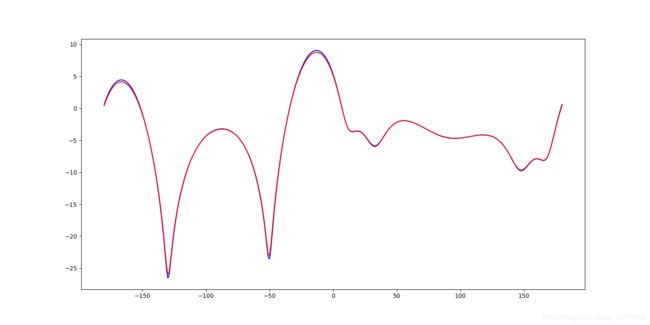
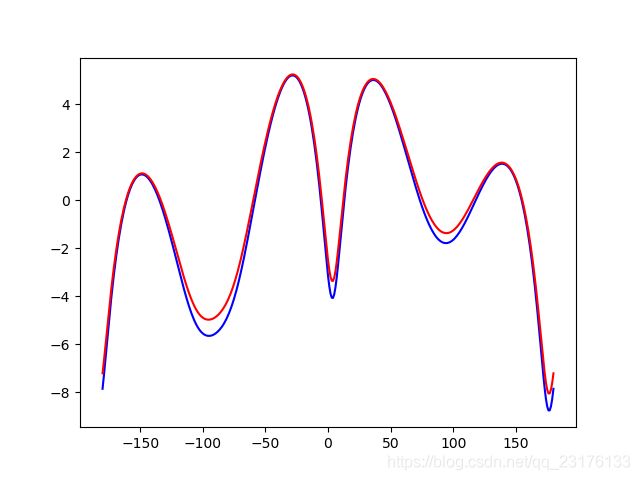
对少数量，中等数量，大数量阵列进行了综合，其中黄色线和红色线是我用Python写的方向图乘积定理综合得到的，蓝色的是hfss综合得到的，基本99%以上的重合，归一化方向图完全一致，最大增益在绝大部分阵列一致，有一小部分有5%左右的差异。

16单元组阵

与HFSS综合完全一致

8单元组阵

与HFSS综合完全一致

5单元组阵

与HFSS综合基本一致

2单元组阵

与HFSS综合基本一致

python实现

先读取单元方向图的数据，然后通过方向图乘积定理综合，写入新的csv，并通过matplot绘制方向图。

#!/usr/bin/env python
# -*- coding:utf-8 -*-
import pandas as pd
import math
import cmath
import csv
import matplotlib.pyplot as plt

class Pattern:
    def radiation(self):
        data_x = []
        data_y = []
        csv_data = pd.read_csv("./data.csv")
        n_data = len(csv_data)

        for i in range(0, n_data):
            data_x.append(csv_data.loc[i][0])
            data_y.append(csv_data.loc[i][1])

        n_cell = 9
        f = 1.575
        position = [0, 94, 206, 281, 393, 475, 587, 683, 785]
        power = [0.2, 0.8, 0.4, 0.3, 0.5, 0.9, 0.2, 0.7, 0.4]
        phase = [0, 82, 165, 201, 247, 229, 262, 305, 334]

        k = 2 * math.pi * f / 300
        csvfile = open("newdata.csv", "w+", newline='')
        writer = csv.writer(csvfile)
        data_array = []
        data_array.append(['Theta [deg]','Power'])
        data_new = []

        for i in range(0, n_data):
            data_array.append([])
            data_array[i+1].append(data_x[i])
            a = complex(0, 0)
            k_d = k * math.sin(data_x[i] * math.pi / 180)
            for j in range(0, n_cell):
                a = a + power[j] * data_y[i] * cmath.exp(complex(0,(phase[j] * math.pi / 180 + k_d * position[j])))
            data_array[i+1].append(10*math.log10(abs(a)))
            data_new.append(data_array[i+1][1])

        writer.writerows(data_array)

        plt.plot(data_x, data_new,"y")
        plt.show()


def main(argv=None):
    pattern = Pattern()
    pattern.radiation()

if __name__ == '__main__':
    main( )

运行结果

运行结果：增益和副瓣波形包络完全一致，只是副瓣的波峰略有差异。