AcWing 1148 秘密的牛奶运输

题目描述：

农夫约翰要把他的牛奶运输到各个销售点。

运输过程中，可以先把牛奶运输到一些销售点，再由这些销售点分别运输到其他销售点。

运输的总距离越小，运输的成本也就越低。

低成本的运输是农夫约翰所希望的。

不过，他并不想让他的竞争对手知道他具体的运输方案，所以他希望采用费用第二小的运输方案而不是最小的。

现在请你帮忙找到该运输方案。

注意：：

• 如果两个方案至少有一条边不同，则我们认为是不同方案；
• 费用第二小的方案在数值上一定要严格小于费用最小的方案；
• 答案保证一定有解；

输入格式

第一行是两个整数 N,M，表示销售点数和交通线路数；

接下来 M 行每行 3 个整数 x,y,z，表示销售点 x 和销售点 y 之间存在线路，长度为 z。

输出格式

输出费用第二小的运输方案的运输总距离。

数据范围

1≤N≤500,
1≤M≤10^4,
1≤z≤10^9,
数据中可能包含重边。

输入样例：

4 4
1 2 100
2 4 200
2 3 250
3 4 100

输出样例：

450

分析：

本题要求严格的次小生成树。我们只需要将最小生成树中某一条边替换为另一条较大的边即可，可以尝试加上每一条非树边，然后去掉多余的边，最后在所有方案中求权值最小的那个就是答案了。

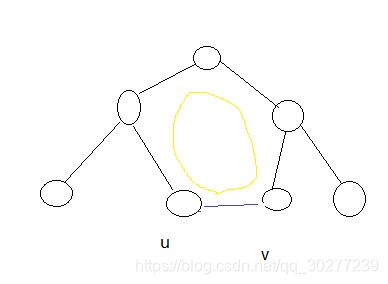
如图所示，我们求出了图的一个最小生成树，然后尝试连接u到v，从而在生成树中u到v的路径加上u到v的这条边就构成了一个环，我们可以删掉生成树中u到v的路径中的任意一条边，就可以生成新的生成树了。由最小生成树的性质知，uv之间的边权一定是这个环上边权最大的一个了，否则就不是最小生成树了，为了生成一棵次小生成树，需要在环中删除那个小于uv边权的边中的最大值。设原最小生成树的边权之和为sum，uv的边权为w，待删除的树边的边权是d，则生成的新的生成树的边权之和为sum + w - d，sum和d是固定的，为了边权之和尽可能的小，则待删去的边权d要尽可能的大，这就解释了为什么要删去环中除w外边权最大的边了。

因为题目要求的是严格意义上的次小生成树，要求新生成树的权值和一定要比最小生成树大，所以在上图的环中如果删除了和w一样大的树边，得到的还是最小生成树，既然不能确定生成树中u到v经过的边的边权都不大于w，那么只好求出u到v的路径中边权的最大值和次大值了，即使最大值等于w，次大值也会小于w。下面的问题就是如何在一棵树中求任意两个节点间路径中最大的边权和次大的边权了，显然可以用dfs遍历来实现。具体实现见代码：

#include 
#include 
#include 
#include 
using namespace std;
const int N = 505,M = 10005;
typedef long long ll;
int n,m,fa[N],m1[N][N],m2[N][N];
int idx,h[N],w[2*M],e[2*M],ne[2*M];
struct Edge{
    int a,b,c;
    bool flag;
    bool operator <(const Edge& ed){
        return c < ed.c;
    }
}edge[M];
void add(int a,int b,int c){
    e[idx] = b,w[idx] = c,ne[idx] = h[a],h[a] = idx++;
}
int find(int x){
    if(x != fa[x])  fa[x] = find(fa[x]);
    return fa[x];
}
//遍历到了u点，u的父节点是p，目前路径中的最大边权是r1，次大边权是r2
void dfs(int u,int p,int r1,int r2,int *s1,int *s2){
    s1[u] = r1,s2[u] = r2;
    for(int i = h[u];~i;i = ne[i]){
        int j = e[i];
        if(j != p){//不用遍历父节点
            int t1 = r1,t2 = r2;
            if(w[i] > t1)   t2 = t1,t1 = w[i];
            else if(w[i] > t2 && w[i] != t1)  t2 = w[i];
            dfs(j,u,t1,t2,s1,s2);
        }
    }
}
int main(){
    scanf("%d%d",&n,&m);
    int a,b,c;
    memset(h,-1,sizeof h);
    for(int i = 0;i < m;i++){
        scanf("%d%d%d",&a,&b,&c);
        edge[i] = {a,b,c,false};
    }
    for(int i = 1;i <= n;i++)   fa[i] = i;
    sort(edge,edge + m);
    ll sum = 0,res = 1e18;
    for(int i = 0;i < m;i++){
        a = find(edge[i].a),b = find(edge[i].b),c = edge[i].c;
        if(a != b){
            fa[a] = b;
            edge[i].flag = true;//树边
            sum += c;
            add(edge[i].a,edge[i].b,edge[i].c);
            add(edge[i].b,edge[i].a,edge[i].c);
        }
    }
    for(int i = 1;i <= n;i++)   dfs(i,-1,-1,-1,m1[i],m2[i]);
    for(int i = 0;i < m;i++){
        if(!edge[i].flag){
            a = edge[i].a,b = edge[i].b,c = edge[i].c;
            if(c > m1[a][b])   res = min(res,sum + c - m1[a][b]);
            else if(c > m2[a][b])   res = min(res,sum + c - m2[a][b]);
        }
    }
    printf("%lld\n",res);
    return 0;
}