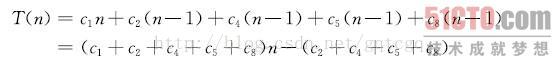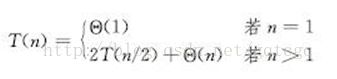1:插入排序:类似于扑克牌,为了将一张牌插入正确的位置,从右向左将它与已在手中的每张牌进行比较,这样,拿在手上的牌就总是排序好的。分析该算法的时间复杂度:
求和:
因此,最好运行时间为:
可以把运行时间表示为an+b。因此这是n的线性函数。
最差运行时间为:
把该最坏情况运行时间表示为an^2+bn+c,因此,它是n的二次函数。
所以,插入排序的时间复杂度为Ө(n^2)。
2:选择排序:首先找出A中的最小元素并将其与A[1]中的元素进行交换。接着,找出A中的次最小元素并将其与A[2]中的元素进行交换。对A中前n-1个元素按该方式继续。选择排序的时间复杂度为Ө(n^2)。
该算法的核心就是找到最小元素的索引index,然后在进行置换。代码如下:
void selectsort(int *set, int num)
{
int i, j, index;
int temp;
for(i = 0; i < num - 1; i++)
{
index = i;
for(j = i+1; j < num; j++)
{
if(set[index] > set[j])
{
index = j;
}
}
temp = set[index];
set[index] = set[i];
set[i] = temp;
}
}
3:归并排序:采用分治策略,将要排序的n个元素分成n/2个元素的子序列,对每个子序列继续分解直到只剩一个元素为止。合并两个已经排好序的子序列。该算法的核心是合并步骤,合并步骤的时间为Ө(n)。总的运行时间递归式如下:
因此,归并排序的时间复杂度为Ө(nlgn)。代码如下:
#define max(x, y) ((x > y)?x:y)
void merge(int *set, int begin1, int end1, int end2)
{
int n1 = end1 - begin1 + 2;
int n2 = end2 - end1 + 1;
int *set1 = malloc(n1 * sizeof(int));
int *set2 = malloc(n2 * sizeof(int));
int maxnum = max(set[end1], set[end2]) + 1;
int i, j;
int k;
for(i = 0; i < n1 - 1; i++)
{
set1[i] = set[begin1 + i];
}
set1[n1 - 1] = maxnum;
for(i = 0; i < n2 - 1; i++)
{
set2[i] = set[end1 + 1 + i];
}
set2[n2 - 1] = maxnum;
i = 0; j = 0;
for(k = begin1; k <= end2; k++)
{
if(set1[i] <= set2[j])
{
set[k] = set1[i];
i++;
}
else
{
set[k] = set2[j];
j++;
}
}
free(set1);
free(set2);
}
void mergesort(int *set, int begin, int end)
{
int mid;
if(begin < end)
{
mid = (end + begin)/2;
mergesort(set, begin, mid);
mergesort(set, mid + 1, end);
merge(set, begin, mid, end);
}
}
4:冒泡排序:反复交换相邻的元素进行排序,把最大的元素放在后面。该算法的时间复杂度为Ө( n^2)。代码如下:
void bubblesort(int *set, int num)
{
int i,j;
for(i = num-1; i > 0; i--)
{
for(j = 0; j < i; j++)
{
if(set[j] > set[j+1])
{
set[j] = set[j] + set[j+1];
set[j+1] = set[j] - set[j+1];
set[j] = set[j] - set[j+1];
}
}
}
}
5:线性查找:依次查找对比数组中的每个元素,看是否与查找值相等。
6:二分查找:对于已经排好序的数组,每次都与中间值对比,然后查找剩下的一半。二分查找的时间复杂度为Ө(lgn)。在插入排序的过程中,因要扫描前面的元素找到合适的位置,如果采用二分查找的方法,尽管查找的时间变短了,但是移动元素的时间还是Ө(n^2)。但是如果该数组是采用链表结构的话,那么移动数组的时间就会变快。代码如下:
int binaryfind(int findarg, int *set, int num)
{
int begin = 0;
int end = num-1;
int mid;
while(begin <= end)
{
mid = (begin + end)/2;
if(set[mid] == findarg)return mid;
else if(set[mid] > findarg)
{
end = mid -1;
}
else
{
begin = mid + 1;
}
}
return -1;
}
7:给定n个元素的集合S,一个整数x,判断在S中是否存在两个元素的和为x。该算法可以先使用归并排序对S进行排序,然后再用二分查找找x – S[i]。所以,该算法的时间复杂度为Ө(nlgn)。