A Demo Allocator——实现一个简单的自定义显式分配器

前言

在本篇博客中，我们拟用C语言实现简单的一个显式分配器，它模拟实现了C标准库中的动态内存分配的过程。我们给出了其详细的设计方案与具体实现，也在文章的最后给出了现实应用中，分配器所采用的一些常见设计。

---

背景知识

首先介绍一下关于动态内存分配的背景知识。

关于分配器

虽然可以使用低级的mmap和munmap函数来创建和删除虚拟内存的区域，但是C程序员还是会觉得当运行时需要额外虚拟内存时，用动态内存分配器 (dynamic memory allocator) 更方便，也有更好的可移植性。

动态内存分配器维护者一个进程的虚拟内存区域，称为堆 (heap) ，对于每个进程，内核维护这一个变量brk，它指向堆的顶部。

分配器有两种基本风格，两种风格都要求应用显式地分配块，它们的不同之处在于由哪个实体来负责释放已分配的块。

显式分配器 (explicit allocator) ，要求应用显式地释放任何已分配的块。例如，C标准库提供一种叫做malloc程序包的显式分配器，并通过调用free函数来释放一个块。C++中的new和delete操作符和C中的malloc和free相当。

隐式分配器 (implicit allocator) ，另一方面，要求分配器检测一个已分配块何时不再被程序所使用，那么就释放这个块。隐式分配器也叫做垃圾收集器 (garbage collector) ，而自动释放为使用的已分配的块的过程叫做垃圾收集 (garbage collecion) 。例如，诸如Lisp、ML以及Java之类的高级语言就依赖垃圾收集来释放已分配的块。

在本篇博客中，我们拟用C语言实现简单的一个显式分配器，它模拟的正是C标准库中的分配与释放内存的过程。

关于虚拟内存

在实现分配器之前，我们需要知道一些关于Linux系统内存管理的基本知识。

为了简单，现代操作系统在处理内存地址时，普遍采用虚拟内存地址技术。即在汇编程序（或机器语言）层面，当涉及内存地址时，都是使用虚拟内存地址。采用这种技术时，每个进程仿佛自己独享一片2^N字节的内存，其中N是机器位数。例如在64位CPU和64位操作系统下，每个进程的虚拟地址空间为2^64Byte。

这种虚拟地址空间的作用主要是简化程序的编写，及方便操作系统对进程间内存的隔离管理，真实中的进程不太可能（也用不到）如此大的内存空间，实际能用到的内存取决于物理内存大小。

由于在机器语言层面都是采用虚拟地址，当实际的机器码程序涉及到内存操作时，需要根据当前进程运行的实际上下文将虚拟地址转换为物理内存地址，才能实现对真实内存数据的操作。这个转换一般由一个叫MMU （Memory Management Unit） 的硬件完成。

那么，对于一个进程来说，内核又是如何维护它的内存分配呢？

我们以64位的Linux系统为例，假设实际用到的内存地址为空间为0x0000000000000000 ~0x00007FFFFFFFFFFF和0xFFFF800000000000 ~ 0xFFFFFFFFFFFFFFFF，其中前面为用户空间 (User Space) ，后者为内核空间 (Kernel Space) 。图示如下：

对用户来说，主要关注的空间是User Space。将User Space放大后，可以看到里面主要分为如下几段：

• Code：这是整个用户空间的最低地址部分，存放的是指令（也就是程序所编译成的可执行机器码）
• Data：这里存放的是初始化过的全局变量
• BSS：这里存放的是未初始化的全局变量
• Heap：堆，这是我们本文重点关注的地方，堆自低地址向高地址增长，后面要讲到的brk相关的系统调用就是从这里分配内存
• Mapping Area：这里是与mmap系统调用相关的区域。大多数实际的malloc实现会考虑通过mmap分配较大块的内存区域，本文不讨论这种情况。这个区域自高地址向低地址增长
• Stack：这是栈区域，自高地址向低地址增长

一般来说，malloc所申请的内存主要从Heap区域分配（本文不考虑通过mmap申请大块内存的情况）。

---

堆与系统级调用

堆

在上文中我们也提到了，Linux维护一个break指针，这个指针指向堆空间的某个地址。

如下图所示，从堆起始地址到break之间的地址空间为映射 (mapped region) 好的，可以供进程访问；而从break往上，是未映射 (unmapped region) 的地址空间，如果访问这段空间则程序会报错。

brk与sbrk

我们希望通过直接调用系统级函数来实现分配器的功能，因此就需要在分配和释放内存时，改变brk指针的位置。

Linux通过brk和sbrk系统调用操作break指针。两个系统调用的原型如下：

int brk(void *addr);
void *sbrk(intptr_t increment);

brk将break指针直接设置为某个地址，而sbrk将break从当前位置移动increment所指定的增量。

brk在执行成功时返回0，否则返回-1，并设置errno为ENOMEM；sbrk成功时返回break移动之前所指向的地址，否则返回(void *)-1。

一个小技巧是，如果将increment设置为0，则可以获得当前break的地址。

这两个系统级函数应如何使用呢？我们先编写一个最简单的malloc函数：

#include 
#include 
void *malloc(size_t size)
{
    void *p;
    p = sbrk(0);
    if (sbrk(size) == (void *)-1)
        return NULL;
    return p;
}

这个malloc每次都在当前break的基础上增加size所指定的字节数，并将之前break的地址返回。

当然，这个malloc由于对所分配的内存缺乏记录，不便于内存释放，所以无法用于真实场景。下面我们就来考虑一个比较完整的分配器设计方案。

---

设计方案

实现目标

首先我们必须明确的是，一个可用的分配器需要达到哪些要求：

• 处理任意请求序列：分配器不可以假设分配和释放请求的顺序，即：一个应用可以有任意的分配请求和释放请求序列，只要满足响应的约束条件。

  注：约束条件指的是——每个释放请求必须对应于一个当前已分配块，这个块是由一个以前的分配请求获得的。对于不满足约束条件的请求，会引起内存管理的错误。现有的C标准库没有对此类错误进行相应的出错预警，我们可以为其添加一些错误处理功能，详见笔者的另一篇博客：An Enhanced Allocator——为C语言的动态内存分配添加出错预警.

• 立即响应请求：不允许分配器为了提高性能而重新排列或者缓冲请求。

• 只使用堆：为了使分配器是可扩展的，分配器使用的任何非标量数据结构都必须保存在堆里。

• 对齐块（对齐要求）：分配器必须对齐块，使得它们可以保存任何类型的数据对象。

• 不修改已分配的块：分配器只能操作或者改变空闲块。

一个实际的分配器要在吞吐率和利用率之间把握好平衡，就必须考虑以下几个问题：

• 空闲块组织：我们如何记录空闲块？

• 放置（适配）：我们如何选择一个合适的空闲块来放置（适配）一个新分配的块？

• 分割：在将一个新分配的块放置到某空闲块之后，我们如何处理这个空闲块中的剩余部分？

• 合并：我们如何处理一个刚刚被释放的块？

下面我们将分别讨论这些问题的实现方案。

数据抽象——隐式空闲链表

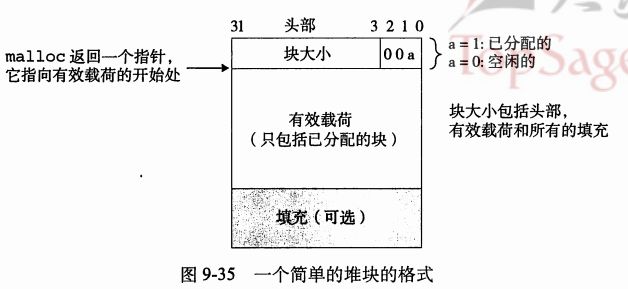
我们首先介绍一种实现分配器比较简单的数据结构：隐式空闲链表 (implicit free lists) ，它将区分块边界、区别已分配块和空闲块的信息，嵌入块本身，在32位操作系统下，其结构如下图所示：

一个块由一个字的头部、有效载荷，以及可能的一些额外的填充组成。头部编码了这个块的大小（整个连续的内存片，包括头部、有效载荷和所有的填充），以及这个块是已分配的还是空闲的。

那么，块的头部究竟蕴含着哪些信息呢？

我们先为内存器强加一个双字的对齐约束条件，在32位操作系统下，这个块大小就总是8的倍数，因此块大小的最低3位就一定是0。所以，我们通过头部这个字的前29位就可以获知块大小，后面的3位就可用来标记这个块是否为空闲。

例如：我们用1来标记已分配的块，用0来标记空闲块，那么如果检测到头部信息为0x00000019的块，将其转化为二进制，即为0000 0000 0000 0000 0000 0000 0001 1001，因此其块大小为11000，即24个字节，其最后的三位001标记了这个块为已分配的块。在这个块首之后的24个字节地址处，我们就可以找到下一个块的头部。

因此，我们可以通过所有块的头部，就可以将堆中所有的块隐含地连接起来。

适配策略

当一个应用请求一个k字节当块时，分配器搜索空闲链表，查找一个足够大可以放置所请求块的空闲块。分配器执行这种搜索方式的常见策略有如下三种：

• 首次适配 (first fit)：从头开始搜索，选择第一个合适的空闲块。

• 下一次适配 (next fit)：从上一次查询结束的地方开始，选择第一个合适的空闲块。

• 最佳适配 (best fit)： 检查每个空闲块，选择适合所需请求大小的最小空闲块。

合并策略

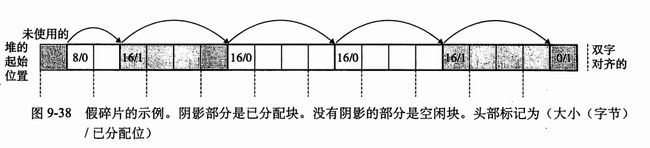
当分配器释放一个已分配块时，可能有其他空闲块与这个新释放的空闲块相邻，这些临界的空闲块可能引起一种现象，叫做假碎片 (fault fragmentation) ，就是有许多空闲块被切割成小的，无法使用的空闲块。如下图所示：

合并 (coalescing) 正是为了解决这一问题，常见的合并策略有如下两种：

• 立即合并 (immediate coalescing) ：在每次一个块被释放时，就合并所有的相邻块。

• 推迟合并 (deferred coalescing) ：等到每个稍晚的时候再合并，如：直到某个分配请求失败时，再扫描整个堆，合并所有的空闲块。

---

具体实现

数据结构

首先我们要确定所采用的数据结构。一个简单可行方案是将堆内存空间以块（Block）的形式组织起来，每个块由meta区和数据区组成，meta区记录数据块的元信息（数据区大小、空闲标志位、指针等等），数据区是真实分配的内存区域，并且数据区的第一个字节地址即为malloc返回的地址。

typedef struct s_block *t_block;
struct s_block {
    size_t size;  /* 数据区大小 */
    t_block next; /* 指向下个块的指针 */
    int free;     /* 是否是空闲块 */
    int padding;  /* 填充4字节，保证meta块长度为8的倍数 */
    char data[1]  /* 这是一个虚拟字段，表示数据块的第一个字节，长度不应计入meta */
};

由于我们只考虑64位机器，为了方便，我们在结构体最后填充一个int，使得结构体本身的长度为8的倍数，以便内存对齐。示意图如下：

适配

我们采用了首次适配的方案：

/* First fit */
t_block find_block(t_block *last, size_t size) {
    t_block b = first_block;
    while(b && !(b->free && b->size >= size)) {
        *last = b;
        b = b->next;
    }
    return b;
}

开辟额外的堆内存

如果现有block都不能满足size的要求，则需要在链表最后开辟一个新的block。这里关键是如何只使用sbrk创建一个struct：

/* 由于存在虚拟的data字段，sizeof不能正确计算meta长度，这里手工设置 */
#define BLOCK_SIZE 24

t_block extend_heap(t_block last, size_t s) {
    t_block b;
    b = sbrk(0);
    if(sbrk(BLOCK_SIZE + s) == (void *)-1)
        return NULL;
    b->size = s;
    b->next = NULL;
    if(last)
        last->next = b;
    b->free = 0;
    return b;
}

分割空闲块

First fit有一个比较致命的缺点，就是可能会让很小的size占据很大的一块block，此时，为了提高payload，应该在剩余数据区足够大的情况下，将其分裂为一个新的block，示意如下：

void split_block(t_block b, size_t s) {
    t_block new;
    new = b->data + s;
    new->size = b->size - s - BLOCK_SIZE ;
    new->next = b->next;
    new->free = 1;
    b->size = s;
    b->next = new;
}

malloc的实现

有了上面的代码，我们可以利用它们整合成一个简单但初步可用的malloc。注意首先我们要定义个block链表的头first_block，初始化为NULL；另外，我们需要剩余空间至少有BLOCK_SIZE + 8才执行分裂操作。

由于我们希望malloc分配的数据区是按8字节对齐，所以在size不为8的倍数时，我们需要将size调整为大于size的最小的8的倍数：

size_t align8(size_t s) {
    if(s & 0x7 == 0)
        return s;
    return ((s >> 3) + 1) << 3;
}

#define BLOCK_SIZE 24
void *first_block=NULL;

void *malloc(size_t size) {
    t_block b, last;
    size_t s;
    /* 对齐地址 */
    s = align8(size);
    if(first_block) {
        /* 查找合适的block */
        last = first_block;
        b = find_block(&last, s);
        if(b) {
            /* 如果可以，则分裂 */
            if ((b->size - s) >= ( BLOCK_SIZE + 8))
                split_block(b, s);
            b->free = 0;
        } else {
            /* 没有合适的block，开辟一个新的 */
            b = extend_heap(last, s);
            if(!b)
                return NULL;
        }
    } else {
        b = extend_heap(NULL, s);
        if(!b)
            return NULL;
        first_block = b;
    }
    return b->data;
}

calloc的实现

有了malloc，实现calloc只要两步：（1）malloc一段内存.（2）将数据区内容置为0.

由于我们的数据区是按8字节对齐的，所以为了提高效率，我们可以每8字节一组置0，而不是一个一个字节设置。我们可以通过新建一个size_t指针，将内存区域强制看做size_t类型来实现。

void *calloc(size_t number, size_t size) {
    size_t *new;
    size_t s8, i;
    new = malloc(number * size);
    if(new) {
        s8 = align8(number * size) >> 3;
        for(i = 0; i < s8; i++)
            new[i] = 0;
    }
    return new;
}

free的实现

free的实现并不像看上去那么简单，这里我们要解决两个关键问题：

• 如何验证所传入的地址是有效地址，即确实是通过malloc方式分配的数据区首地址.
• 如何解决碎片问题

首先我们要保证传入free的地址是有效的，这个有效包括两方面：
- 地址应该在之前malloc所分配的区域内，即在first_block和当前break指针范围内.
- 这个地址确实是之前通过我们自己的malloc分配的.

第一个问题比较好解决，只要进行地址比较就可以了，关键是第二个问题。这里有两种解决方案：一是在结构体内埋一个magic number字段，free之前通过相对偏移检查特定位置的值是否为我们设置的magic number，另一种方法是在结构体内增加一个magic pointer，这个指针指向数据区的第一个字节（也就是在合法时free时传入的地址），我们在free前检查magic pointer是否指向参数所指地址。这里我们采用第二种方案。

首先我们在结构体中增加magic pointer（同时要修改BLOCK_SIZE）：

typedef struct s_block *t_block;
struct s_block {
    size_t size;  /* 数据区大小 */
    t_block next; /* 指向下个块的指针 */
    int free;     /* 是否是空闲块 */
    int padding;  /* 填充4字节，保证meta块长度为8的倍数 */
    void *ptr;    /* Magic pointer，指向data */
    char data[1]  /* 这是一个虚拟字段，表示数据块的第一个字节，长度不应计入meta */
};

然后我们定义检查地址合法性的函数：

t_block get_block(void *p) {
    char *tmp;  
    tmp = p;
    return (p = tmp -= BLOCK_SIZE);
}

int valid_addr(void *p) {
    if(first_block) {
        if(p > first_block && p < sbrk(0)) {
            return p == (get_block(p))->ptr;
        }
    }
    return 0;
}

当多次malloc和free后，整个内存池可能会产生很多碎片block，这些block很小，经常无法使用，甚至出现许多碎片连在一起，虽然总体能满足某此malloc要求，但是由于分割成了多个小block而无法fit，这就是碎片问题。

一个简单的解决方式时当free某个block时，如果发现它相邻的block也是free的，则将block和相邻block合并。为了满足这个实现，需要将s_block改为双向链表。修改后的block结构如下：

typedef struct s_block *t_block;
struct s_block {
    size_t size;  /* 数据区大小 */
    t_block prev; /* 指向上个块的指针 */
    t_block next; /* 指向下个块的指针 */
    int free;     /* 是否是空闲块 */
    int padding;  /* 填充4字节，保证meta块长度为8的倍数 */
    void *ptr;    /* Magic pointer，指向data */
    char data[1]  /* 这是一个虚拟字段，表示数据块的第一个字节，长度不应计入meta */
};

合并方法如下：

t_block fusion(t_block b) {
    if (b->next && b->next->free) {
        b->size += BLOCK_SIZE + b->next->size;
        b->next = b->next->next;
        if(b->next)
            b->next->prev = b;
    }
    return b;
}

free的实现：

void free(void *p) {
    t_block b;
    if(valid_addr(p)) {
        b = get_block(p);
        b->free = 1;
        if(b->prev && b->prev->free)
            b = fusion(b->prev);
        if(b->next)
            fusion(b);
        else {
            if(b->prev)
                b->prev->prev = NULL;
            else
                first_block = NULL;
            brk(b);
        }
    }
}

realloc的实现

为了实现realloc，我们首先要实现一个内存复制方法。如同calloc一样，为了效率，我们以8字节为单位进行复制：

void copy_block(t_block src, t_block dst) {
    size_t *sdata, *ddata;
    size_t i;
    sdata = src->ptr;
    ddata = dst->ptr;
    for(i = 0; (i * 8) < src->size && (i * 8) < dst->size; i++)
        ddata[i] = sdata[i];
}

下面是realloc的实现：

void *realloc(void *p, size_t size) {
    size_t s;
    t_block b, new;
    void *newp;
    if (!p)
        /* 根据标准库文档，当p传入NULL时，相当于调用malloc */
        return malloc(size);
    if(valid_addr(p)) {
        s = align8(size);
        b = get_block(p);
        if(b->size >= s) {
            if(b->size - s >= (BLOCK_SIZE + 8))
                split_block(b,s);
        } else {
            /* 看是否可进行合并 */
            if(b->next && b->next->free
                    && (b->size + BLOCK_SIZE + b->next->size) >= s) {
                fusion(b);
                if(b->size - s >= (BLOCK_SIZE + 8))
                    split_block(b, s);
            } else {
                /* 新malloc */
                newp = malloc (s);
                if (!newp)
                    return NULL;
                new = get_block(newp);
                copy_block(b, new);
                free(p);
                return(newp);
            }
        }
        return (p);
    }
    return NULL;
}

---

现实应用

至此，我们通过实现一个简单的显式分配器，学习了动态内存分配背后的机制。当然与现有C的标准库实现（例如glibc）相比，我们实现的malloc并不是特别高效，但是这个实现比目前真实的malloc实现要简单很多，因此易于理解。重要的是，这个实现和真实实现在基本原理上是一致的。

关于真实世界中malloc的实现，可以查阅 glibc 给出的源码。除此之外，我们接下来将从其他的方面，再简要分析一下现实应用中的分配器实现特点。

适配策略

在上文中我们提到了首次适配、下一次适配和最佳适配这三种策略，我们先权衡一下它们的优劣：

策略	优势	劣势
首次适配	将大的空闲块保留在链表的后面	靠近链表起始处的碎片多
下一次适配	比首次适配运行起来快一些	内存利用率比首次适配低得多
最佳适配	内存利用率最高	需要对堆进行彻底的搜索，耗时最长

在现实应用中，有一些非常精细复杂的分离式空闲链表组织，它接近于最佳适配策略，不需要进行彻底地堆搜索，从而在内存利用率、搜索时间都有较好的应用效果。

合并策略

除了适配策略外，我们还提到了立即合并与推迟合并这两种合并策略。

我们的Allocator使用了立即合并的策略，它简单明了，可以在常数时间内完成，但是对于某些请求模式，这种方式会产生一种形式的抖动，块会反复地合并，然后马上分割。

如下图所示：如果反复地分配和释放一个3个字的块，将产生大量不必要的分割和合并。

因此，在现实应用中，快速的分配器通常会选择某种形式的推迟合并。

显式空闲链表

对于显示分配器来说，除了我们的Allocator中使用的隐式空闲链表（尽管我们最终的数据结构使用了双向链表的形式，而不是一个简单的头部，但这依然是把所有的已分配块与空闲块连接在一起，因此依然是隐式的），它为我们提供了一种介绍基本分配器概念的简单方法，然而，因为块分配与堆块的总数呈线性关系，所以对于通用的分配器，隐式空闲链表是不适合的。

我们下面将分别讨论显式空闲链表和分离的空闲链表，它们都对空闲块进行了不同于隐式空闲链表的组织方法。

上图中的显式空闲链表，把分配块和空闲块用不同的数据结构进行组织，每个空闲块中，包含一个前驱和后继指针，所有的空闲块形成了一个双向空闲链表，如果我们依然采取首次适配的方式，那么分配时间就可以从块总数的线性时间减少到了空闲块数量的线性时间。

分离的空闲链表

通过显式空闲链表，我们将分配时间就从块总数的线性时间减少到了空闲块数量的线性时间。采用分离存储 (segregated storage) 的方式，可以进一步减少分配的时间。

分离存储，就是维护多个空闲链表，其中每个链表中的块有大致相等的大小。一般的思路是将所有可能的块大小分成一些等价类，也叫做大小类 (size class)。

我们只简要介绍两种最基本的方法：简单分离存储 (simple segregated storage) 和分离适配 (segregated fit) 。

• 简单分离存储
  每个大小类的空闲链表包含大小型等的块，每个块的大小就是这个大小类中最大元素的大小。
  优点：分配和释放块都是很快的常数时间操作。
  缺点：很容易造成内部和外部碎片。

• 分离适配
  分配器维护这一个空闲链表的数组，每个空闲链表适合一个大小类相关联的，并且被组织成某种类型的显式或隐式链表。
  这种方法既快速，对内存的使用也很有效率。C标准库中提供的GNUmalloc包就是采用这种方法。

---

参考资料

[1] 《C和指针》. [美] Kenneth A.reek 著.

[2]《深入理解计算机系统》（第3版）. Randal E. Bryant, David R.O’Hallaron 著.

[3] 博客：如何实现一个malloc.

[4] 《A Malloc Tutorial》.

[5] 真实世界的malloc实现——glibc.