软件构造实验二

前言：这次实验相比于第一次实验难度高了不少，主要是以前还没有这样从头到尾地设计过ADT，不是很清楚哪里该怎么做。前几天终于把实验写完了，趁还有记忆先把这次实验总结一下。

P1 Poetic Walks

MIT的指导页面链接如下：
http://web.mit.edu/6.031/www/sp17/psets/ps2/
仔细阅读MIT的指导页面发现，该问题已经将ADT的大体框架提供给我们，Graph的接口，边和顶点的两种具体实现形式，我们要做的就是按照规约去实现具体功能，并将ADT泛型化（需要了解接口、泛型的概念），在过程中贯穿着测试优先的理念，Problem 4中的诗歌其实就是考察我们在设计好ADT之后，具体应用ADT的能力。

Problem 1: Test Graph

1.首先是静态方法测试：我直接使用了他提供的两个测试方法，未作修改，由于有两种实现方式，在测试时只需要令Graph中的empty方法返回ConcreteEdgesGraph或者ConcreteVerticesGraph中的一个新对象即可，我这里选择ConcreteEdgesGraph，如图：
完成以后进行测试：

2.之后是对图接口中各个方法的测试，Graph接口中各个方法已经给出规约，按照规约进行输入域的等价类划分，进行测试用例设计，值得注意的是，这是黑盒测试，只需按照规约设计，与接口的具体实现方式无关。也就是说无论是边的实现方式还是顶点的实现方式，测试都应该是适用的。测试策略如下
// Testing strategy
// Test add: add new vertex;add vertex that has existed
// Test set: 1.both vertices are in the graph;one is in the graph and another is not;neither is in the graph
// 2.reset the edge is in the graph; edge is not in the graph;
// 3.weight=0; weight>0; weight<0;
// Test remove: 1.vertex is in the graph; vertex is not in the graph;
// 2.remove vertex with edges; remove vertex without edges;
// Test vertices: empty graph;graph with n vertices(n>0)
// Test sources: empty graph;graph with n vertices(n>0)
// Test targets: empty graph;graph with n vertices(n>0)

Problem 2: Implement Graph

1.ConcreteEdgesGraph

1）.先介绍Edge类，这是实现ConcreteEdgesGraph类的基础。

按指导要求，Edge类必须是不可变类型，因此将属性全部设置为私有和final。每条边的权值，按要求都必须为正值，因此checkRep检查边是否权值为正
private void checkRep() {
assert weight>0;
}
该类中其余的方法都是基本的构造函数以及get方法，以及对toString函数进行了重写，使之能够正确显示Edge的信息：起点->终点：边权值
2）.再介绍ConcreteEdgesGraph类
// Abstraction function:
// represents the graph with vertices and positive directed edges
// Representation invariant:
// vertices contains different graph vertices
// edges has instinct direction and positive weight
// Safety from rep exposure:
// All fields are private and final
// change the return value to unmodifiable type when needed to return changeable fields
该类的属性已经由MIT给定，包括顶点集合以及边集。
1.检查不变量：边集中每一条边都要为正权值private void checkRep() {
for(Edge e:edges) {
assert e.getweight()>0;
}
}

2.实现Graph接口中add函数
利用顶点属性是一个集合的特点，如果顶点本身已经存在，便不会再加入到集合中，反之可以顺利加入，因此可以直接调用集合类中的add函数

3.实现Graph接口中set函数
由于顶点存储在集合里，而set的边的两个顶点本身可能未加入到图中，因此先直接调用集合add函数将两个顶点加入图中，即使图中存在也不会重复添加。
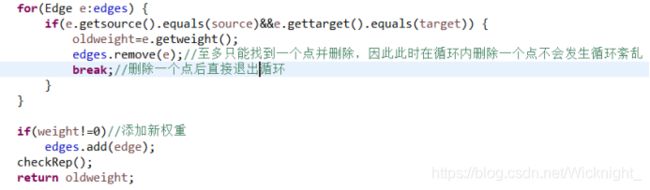
然后在边集中遍历，如果找到了一条同样起点和终点的边，返回权值并将其删除如果没找到，权值始终是0。如果参数weight为0，则已完成删除操作，直接返回旧权值即可。如果不为0，将新边加入边集，然后返回旧权值。

4.实现Graph接口中remove函数
首先将指定顶点在顶点集合中删除，然后遍历边集，凡是以指定顶点作为起点或终点的边，都将其删除

5.实现Graph接口中vertices函数
由于成员变量中已经包含顶点集合，因此直接返回该集合即可，但为了防止表示泄露，将返回集合转换为不可变类型。

6.实现Graph接口中sources函数
依据规约，我们要找到所有以指定点作为终点的边，因此我们新建一个map，遍历边集，凡是遇到这样的边，就将 起点-权值键值对加入map，遍历完成后返回即可。由于该map本身与图的成员变量无引用关系，因此无需转换为不可变类型。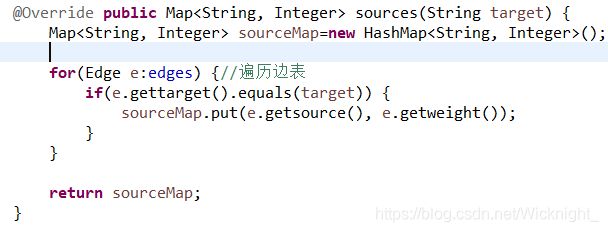
7.实现Graph接口中targets函数
同6的实现，只不过指定点作为起点，仍是遍历边集即可
8.toString函数
逐个调用每条边的toString函数

2.ConcreteVerticesGraph

1）.首先介绍Vertex类
根据要求，该类为可变类，因为每个顶点的边数是动态变化的，但一定要注意表示泄露问题，这种可变并不是可以将属性暴露给用户让用户实现“变化”，而应该是在类的内部提供实现变化的方法，用户通过调用这些方法实现“可变”，因此我设计了addedge和removeedge方法，实现顶点出边的动态变化，并将get方法中的返回值使用防御式拷贝。

每一个Vertex记录顶点自己的标签以及该顶点的所有出边，为了节省存储空间我并没有存储入边。
// Abstraction function:
// represents one vertex and its adjacent out edges of graph
// Representation invariant:
// only one edge between two vertices
// Safety from rep exposure:
// All fields are private and defensive programming
在起点确定的情况下，每两个顶点间都应该只存在一条有向边，即为表示不变量，因此checkRep中建立一个出边终点集合，它的大小应该等于出边集map的大小

addedge函数是向出边集中添加一条新的有向边（如果该边已存在就忽略）
removeedge函数是移除出边集中一条指定的有向边（该边必须在图中）

toString函数同样进行重写，以将每个顶点关联的出边全部打印：

2）然后介绍ConcreteVerticesGraph类的实现：
// Abstraction function:
// represents graph:different vertices and their adjacent out edges
// Representation invariant:
// vertices different from each other
// Safety from rep exposure:
// field is private and final and change the return value to unmodifiable type when needed to return changeable fields

1.add函数
遍历顶点list，如果存在顶点标签与该顶点标签相同，无需添加，否则，添加进顶点list

2.set函数
先在顶点list中遍历找到起点，用index记录下标，如果找到了起点，在起点的边集中遍历，若是找到了连接终点的边，记录权值并删除之后根据index的值判断是否存在起点，不存在时，将其加入list如果weight为0，此时删除操作已完成，若不为0，将新权值的边加入之后为了防止终点原来不存在于图中，调用add函数将终点加入图中，最后返回旧权值

3.remove函数
两次遍历顶点list，一次找到指定顶点，将其移除出list；由于我设计的Vertex类只保存了出边，因此需要第二次遍历所有顶点，删除入边

4.vertices函数
只需创建一个set，遍历顶点list，将所有顶点的标签加入set即可

5.sources函数
新建一个map，遍历顶点list，对于每一个顶点都遍历出边集，如果出边中包括该终点，将这条边加入map，最后返回这个map，为了防止表示泄露，将其转换为不可变类型返回

6.targets函数
遍历顶点集，找到指定顶点，然后复制其出边集即可，为了防止表示泄露，将其转换为不可变类型返回

7.toString逐个调用每一个顶点的toString即可，所有的出边即构成了图的所有边

Problem 3: Implement generic Graph

1.用泛型代替String类型，类的声明中加上,同时顶点的标签改为L类型
2.Implement Graph.empty()
在两种实现方式中任选一种创建实例即可，我这里选择ConcreteEdgesGraph的实现方式

Problem 4: Poetic walks

1.测试策略：
①根据规约，构造函数中完成了从文件读取信息并保存在图中的功能，测试策略从可根据规约进行提取：大小写不敏感–大写输入，小写输入；可有重复输入–存在重复词，无重复词；
②对于poem函数，根据桥词的不同情况来进行测试：输入字符串在图中已存储，输入字符串未在图中存储；输入之间没有桥词可插入；输入有唯一桥词可插入；多桥词要选最大权值，因此测试：多桥词情况；单桥词情况其中我将poem中部分功能单独写成了hasbridge函数，测试策略可沿用以上策略
③我还改写了toString函数以正确向client显示存储的信息，设计一般用例测试即可

3.GraphPoet
①首先逐行读取文件，将大写全部转化为小写。获得长度以后用一个循环遍历，对于每两个相邻词进行处理，判断两个单词是否已经在图中有邻接边。
②如果有邻接边说明已经多次出现，得到旧权值后再+1，调用set函数
③如果没有邻接边说明第一次出现该邻接关系，直接set权值为1的边
④需要注意的是对于每一行结尾字符串的处理，每一行的结尾认为是与下一行的开头相邻接的，因此每一行都要记录结尾字符串，下一行开始时先判断起始字符串与该结尾字符串的关系。这也是我单独处理第一行的原因，需要先用第一行得到一个结尾，这样后续行才能接着利用循环进行处理

4.Graph poetry slam
①由于图中存储的都是小写单词的结点信息，对于输入字符串先按照空格分词，然后转化为全小写副本。
②新建一个初始为空的输出字符串，然后遍历每一个单词。
③如果两个单词全部都在图中，调用hasbridge函数判断二者之间是否有桥词，有桥词则将首单词、桥词、尾单词依次插入输出字符串中，无桥词则将两个单词直接插入输出中；
④如果二者之一未在图中，直接原封不动的插入到输出中
其中hasbridge是判断两个词之间是否存在桥词的功能方法，我将其分离出来：

根据起点直接调用targets函数得到所有出边，遍历出边，以每一条出边的终点再利用targets得到出边，如果这次得到的出边中含有指定终点，说明在图中两个顶点之间有桥词存在，记录下来，因为可能存在多个桥词，要从中选取最大权重的桥词；如果不存在桥词，则返回和顶点标签相同的字符串。

P2 Re-implement the Social Network in Lab1

该任务主要是训练我们在设计好ADT之后应用ADT解决问题的能力，person类的实现直接沿用，friendshipgraph则可以继承图的一种实现方式，复用Graph中的函数重新实现，相对来说比较简单

1.FriendshipGraph类

继承ConcreteEdgesGraph，利用父类方法实现功能。
addVertex函数，调用父类add函数即可，另外加入重名处理。
addEdge函数，调用父类的set函数，另外加入重复边的处理
getDistance函数，与实验一中的实现思路相同，采用广度优先搜索+队列的方式，新建两个列表：nowList和friendList，只不过这里对于邻接边的存储方式发生变化，我在实验一中采取的是定长数组的实现方式，这里的边存储已经在父类中实现。另外获得一个顶点的邻接边时可以直接利用父类的targets方法，非常方便。

2.Person类

沿用实验一中的Person类，两个属性：name与visit。
visit是用来标记在计算距离的遍历时其是否被访问过。
一个构造方法：根据名字构建对象
以及相关的get、set方法，对visit进行初始化的方法
同时对equals方法和hashCode方法进行重写便于在加入顶点时判断重名

实验未要求Person类的测试用例，因此这里简单用main函数测试一下，重名判断效果

客户端与测试用例按实验要求直接沿用实验一中部分即可。

P3 Playing Chess

1.ADT设计/实现方案

这里由小的方面向大的方面逐步阐述

一.Position类这是最基本的一个ADT，它代表了棋盘上的一个基础的位置坐标，有x和y两个维度，位置一旦确定，不能再进行修改，设计为不可变类。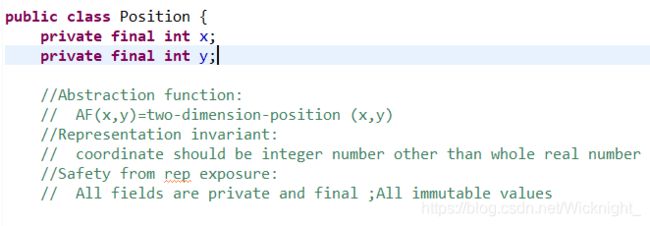
函数为基本的构造函数和get函数

二．Piece类

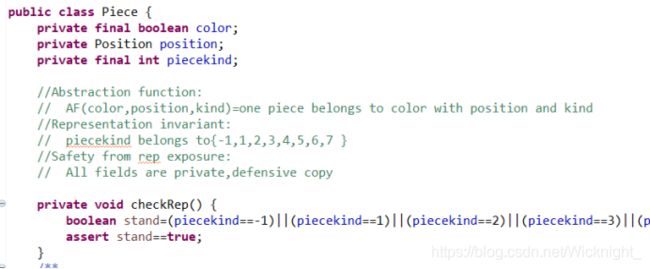
1）.拥有三个成员变量，其中color表明棋子是黑棋还是白旗，position是棋子的位置坐标，piecekind表明棋子的类型，是用来检测异常的错误棋子（-1），还是围棋（1），亦或是国际象棋（2-7）。
由于在游戏进行过程中会有移动棋子，移除棋子等操作，因此要求棋子的位置坐标应该是可变的，故为可变类。
2）.仅在构造方法时会对piecekind进行赋值，因此在此时进行checkRep
3）.常规的get方法以及对pisition实现改变的set方法这里不多作介绍
4）.采用了防御式拷贝以防表示泄露

三.Player类

1）.拥有三个成员变量，color表明棋手执白棋（true）还是黑棋（false），利用这一点与棋子建立联系；name是棋手的姓名，在游戏中会由玩家在命令行输入，history记录棋手的走棋历史，每成功执行一次操作变添加
2）.常规构造方法与get方法
3）.对于history有一些特殊方法：
首先，由于棋手的走棋历史会随对局进行动态变化，因此需要设计添加走棋历史的方法，Player也为可变类。

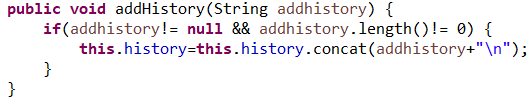
其次，当国际象棋棋盘初始化时通过棋手的操作来实现32个棋子的初始化，因此会添加走棋历史，但这其实并不属于棋手真正的走棋历史，因此需要清空，便设计了清空走棋历史的方法

四.Board类

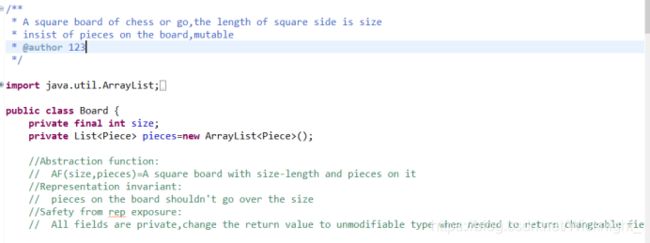
1）. 两个成员变量，size表示棋盘的边长，pieces列表是存储棋盘上已经存在的棋子的动态数组。棋盘大小一经确定不能更改，为final属性；由于棋盘上棋子需要动态变化，需要提供变值器，因此为可变类
2）. 构造函数与get函数

为了防止表示泄露，将list返回为不可变类型3）. checkpositon方法
判断一个给定坐标是否越界，为了将各个大功能细化而抽离出的方法
4）haspiece方法
给定一个坐标，判断该坐标处有无棋子，越界时返回-2，无棋子返回-1，否则返回棋子在list中的下标（加入棋盘的顺序）
5）getpiece函数
给定棋子加入棋盘的顺序i，返回list中棋子，越界时返回一个kind为-1的错误棋子，5和4连用得到指定坐标处棋子
6）putpiece函数
将一个棋子放置在棋盘的指定位置，考虑了多种异常情况：棋子不属于指定棋手，位置越界，位置已存在棋子，进行分别处理；添加成功时返回true，该方法是落子，吃子的基础方法

7）.removepiece函数
将指定位置处的棋子删除，仅当位置合法，指定位置处有棋子且棋子属于操作的棋手时能够成功移除并返回true，该方法是提子，吃子的基础方法
8）.printboard函数
利用一个二重循环将size*size的棋盘打印出来，通过haspiece可判断指定坐标有无棋子。需要注意的是由于存储的棋盘和玩家观察的棋盘上下颠倒，因此打印时需要行逆序打印

五. Action类

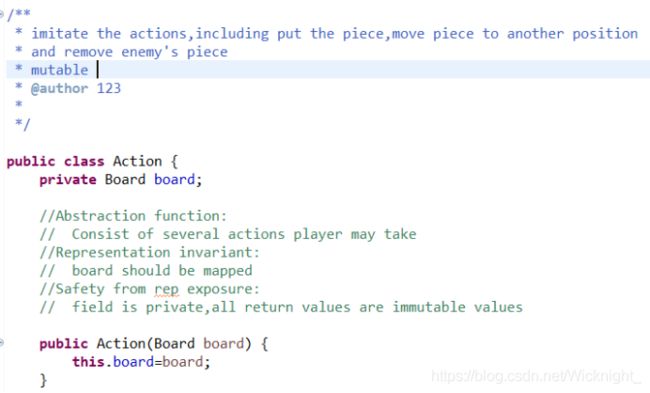
1）. 只有一个棋盘属性，因为行为都是针对棋盘以及棋盘上的所有棋子的
2）. put（落子）
Put是将棋子置于指定位置，可以直接调用board中实现的putpiece函数，放置成功时添加走棋历史

3)move（移动棋子）
move实现将一个位置处棋子移动到另一个位置处棋子，是针对国际象棋的。考虑了多种异常情况：
①先判断两个位置是否相同
②判断原位置处棋子：是否越界、是否有棋子、是否属于棋手
③判断目标位置：是否越界、是否存在棋子
④条件均满足则先删除再放置到新位置，最后添加走棋历史。
⑤注意这里不能直接利用board中实现的removepiece和putpiece方法的返回值来判断原位置以及目标位置情况，假设原位置处棋子满足条件，但目标位置不满足，如果是直接用remove返回值判断，返回true的同时已经将棋子删除，但实际上操作不应该进行。因此一定要先判断两个条件是否满足，都满足时才能调用这两个函数

4)pickup（提子）
由于是移除对手的棋子，因此要先构造一个执相反棋的棋手，之后调用board中removepiece方法即可
5）eatchess（吃子）
整体过程与move动作相似，需要判断原位置、目标位置两个位置的情况，不同的是这次目标位置应该存在对方棋子，同样不能直接调用removepiece函数以及putpiece函数，而是先判断两个条件是否都满足。这里不再赘述

六. Game类
最高层次的抽象，包含正常对局的所有基本信息，是前五个类的一个抽象整合，为client建立与底层ADT交互的方法接口

1). 包含之前所有ADT的基本信息，棋盘，两个玩家，在对局中提供给玩家的可能动作，另外，gamekind表示对局类型，true表示围棋，false表示国际象棋两个常量gosize,chesssize分别表示围棋棋盘、国际象棋棋盘的边长
2).
//Abstraction function:
// represents a game of chess or go,determined by gamekind,with a gameboard,and two players and
// actions that could be taken of the game
//Representation invariant:
// gameboard,p1,p2 should be mapped,two player’s name should be different
//Safety from rep exposure:
// All fields are private,all return values are immutable values
表示不变量要求两个玩家的姓名必须不同，因此

3)构造函数

确定对局类型，玩家姓名后即可初始化棋盘与玩家，动作，其中注意的是如果为国际象棋游戏，需要额外对棋盘进行初始化，因此设计了initBoard函数

由于是利用put操作初始化，因此会添加历史，所以需要清空玩家历史
4) 提供动作的“方法接口”：put、move、pickup、eatchess
调用action中相应的方法，并对异常情况再打印一些提示信息即可另外，printboard打印棋盘也可直接调用属性gameboard中printboard方法即可
5)querypiece方法：查询某一位置棋子信息：空闲、哪个棋手的什么棋子
6)countpiece方法：计算某棋手在棋盘上一共还拥有多少棋子
用count变量保存总和，初始化为0;遍历gameboard棋盘，遇到该棋手棋子便加1
7)printhistory方法：打印某一棋手的走棋历史
打印对应棋手的getHistory函数即可

2.主程序MyChessAndGoGame设计/实现方案

除了main函数之外分别设计了go方法以及chess方法分别处理围棋游戏与国际象棋游戏与玩家的交互，在main中实现调用
在main函数中先从玩家处获得游戏对局的基本信息，如游戏类型、玩家姓名等，创建Game类对象后根据游戏类型调用二者之一。
利用一个boolean变量记录每一回合的执棋手，true为白棋棋手，false为黑棋棋手，每执行一回合后令turn=!turn
对于各种功能实现的演示截图如下：
①围棋起始功能菜单：

②围棋落子：空格分词后匹配put功能，则对第二个字符串按照“,”进行split分词得到x,y坐标，然后调用game的put函数即可
③围棋提子：空格分词后匹配到pick功能，则对第二个字符串按照“,”进行split分词得到x,y坐标，然后调用game的pickup函数即可

④围棋查询棋子：空格分词后匹配到query功能，则对第二个字符串按照“,”进行split分词得到x,y坐标，然后调用game的querypiece函数即可

⑤围棋打印棋盘：

⑥围棋计算棋子数：匹配后直接调用game中的countpiece函数

⑦围棋结束&走棋历史：
⑧国际象棋功能菜单

⑨国际象棋print&初始化效果

⑩国际象棋move：空格分词得到三个字符串，对后两个字符串进行关于”,”的split分词，得到两个坐标，然后调用game中的move函数

⑪国际象棋eat（吃子）：空格分词得到三个字符串，对后两个字符串进行关于”,”的split分词，得到两个坐标，然后调用game中的eat函数

⑫国际象棋query：空格分词得到两个字符串，对后一字符串进行关于”,”的split分词，得到坐标，然后调用game中的querypiece函数

⑬国际象棋count计算棋子数：调用game中的countpiece函数

⑭国际象棋end&走棋历史

3.ADT和主程序的测试方案

一．Position、Piece、Player类的方法为基础的构造函数、get方法等，只需用一般实例测试即可

二．对于Board类测试时，多与棋子有关，棋子位置是否越界，棋子与棋手的关系，指定位置是否存在棋子为主要考察情况，针对合法及非法输入进行分别验证
//Test strategy:棋子不属于棋手；棋子属于棋手
// 指定位置已有棋子 ；指定位置无棋子
// 指定位置越界；指定位置合法

三．对于Action类的测试便是测试四个行为方法，现将每个方法的测试策略分别列出：
1). put:
//Test strategy:棋子不属于棋手；棋子属于棋手
// 指定位置已有棋子 ；指定位置可正常放置新棋子
// 指定位置越界；指定位置合法
2). move:
//Test strategy:初始位置棋子不属于棋手或无棋子；初始位置棋子属于棋手
// 两个位置相同；两个位置不同
// 指定位置已有棋子 ；指定位置可正常放置新棋子
// 指定位置越界；指定位置合法
3). pickup:
//Test strategy:所提棋子不属于对方；所提棋子属于对方
// 指定位置无棋子可提 ；指定位置可正常提取棋子
// 指定位置越界；指定位置合法
4). eatchess:
//Test strategy:第二个位置无棋子；第二个位置上棋子不属于对方；第二个位置棋子属于对方
// 第一个位置无棋子 ；第一个位置棋子不属于该棋手；第一个位置棋子属于该棋手
// 指定位置越界；指定位置合法
// 两个位置相同；两个位置不同

四．Game类测试
对于那种“方法接口”比如put，printboard，其实都是调用其余类的方法，测试策略相同，可额外增添一条测试策略：针对围棋游戏/国际象棋游戏