【机器学习】 Local Outlier Factor(LOF)算法
【机器学习】 Local Outlier Factor(LOF)算法
- 参考
- LOF算法
- k-distance:第k距离
- k-distance neighborhood of p:第k距离邻域
- reach-distance:可达距离
- local reachability density:局部可达密度
- local outlier factor:局部离群因子
- python中LOF算法的使用
- 结语
参考
局部异常因子算法-Local Outlier Factor(LOF)
Outlier detection with Local Outlier Factor (LOF)
LOF算法
局部异常因子LOF算法(Local Outlier Factor),是一种基于距离的异常检测算法。
理解LOF算法可以从理解下面几个概念开始:
k-distance:第k距离
d ( p , o ) d(p, o) d(p,o)代表点 p p p和点 o o o之间的距离
点 p p p的第k距离: d k ( p ) = d ( p , o ) d_k(p) = d(p,o) dk(p)=d(p,o), o o o是距离 p p p第k远的点(不包括 p p p自身)

上图 d 5 ( p ) d_5(p) d5(p)表示 p p p的第5距离
k-distance neighborhood of p:第k距离邻域
点 p p p的第k距离邻域 N k ( p ) N_k(p) Nk(p),就是 p p p的第k距离以内的所有点的个数,包括第k距离上的点,不包括点 p p p
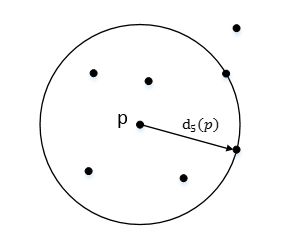
上图中 N 5 ( p ) = 6 N_5(p) = 6 N5(p)=6
reach-distance:可达距离
点 o o o到点 p p p的第k可达距离定义为:
r e a c h reach reach- d i s t a n c e k ( o , p ) = m a x { 点 o 的 第 k 距 离 , o 到 p 的 距 离 } distance_k(o,p) = max \lbrace{点o的第k距离,o到p的距离\rbrace} distancek(o,p)=max{点o的第k距离,o到p的距离}
注意上面提到的是:点 p p p的第k距离、点 p p p的第k距离邻域,圆心是 p p p
这里提到的是:点 o o o到点 p p p的第k可达距离,圆心是 o o o
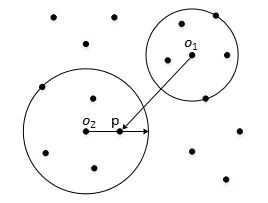
上图中, r e a c h reach reach- d i s t a n c e 5 ( o 1 , p ) = 点 o 1 到 点 p 的 距 离 distance_5(o_1,p) = 点o_1到点p的距离 distance5(o1,p)=点o1到点p的距离
上图中, r e a c h reach reach- d i s t a n c e 5 ( o 2 , p ) = 点 o 2 的 第 5 距 离 distance_5(o_2,p) = 点o_2的第5距离 distance5(o2,p)=点o2的第5距离
local reachability density:局部可达密度
点 p p p的第k距离局部可达密度表示为:
点 p p p的第k距离临域中所有的点,这些点到点 p p p的第k可达距离的平均值的倒数
注意这里圆心是点 o o o,点 o o o是点 p p p的第k距离临域中的点
l r d k ( p ) = N k ( p ) p 的 第 k 距 离 邻 域 中 所 有 的 点 , 这 些 点 到 p 的 第 k 可 达 距 离 的 和 lrd_k(p) = \dfrac{N_k(p)}{p的第k距离邻域中所有的点,这些点到p的第k可达距离的和} lrdk(p)=p的第k距离邻域中所有的点,这些点到p的第k可达距离的和Nk(p)
这个值的含义可以这样理解,首先这代表一个密度,密度越高,我们认为越可能属于同一簇,密度越低,越可能是离群点。
如果 p p p和周围邻域点是同一簇,那么可达距离越可能为较小的 d k ( o ) d_k(o) dk(o),导致可达距离之和较小,密度较高;如果p和周围邻域点较远,那么可达距离可能都会取较大值 d ( o , p ) d(o,p) d(o,p),导致密度较小,越可能是离群点。
local outlier factor:局部离群因子
点 p p p的局部离群因子表示为:
点 p p p的第k距离邻域 N k ( p ) N_k(p) Nk(p)中所有的点,这些点的第k距离局部可达密度的平均值,与点 p p p的第k距离局部可达密度的比值
L O F k ( p ) = 点 p 的 第 k 距 离 邻 域 N k ( p ) 中 所 有 的 点 , 这 些 点 的 第 k 距 离 局 部 可 达 密 度 的 平 均 值 点 p 的 第 k 距 离 局 部 可 达 密 度 LOF_k(p) = \dfrac{点p的第k距离邻域N_k(p)中所有的点,这些点的第k距离局部可达密度的平均值}{点p的第k距离局部可达密度} LOFk(p)=点p的第k距离局部可达密度点p的第k距离邻域Nk(p)中所有的点,这些点的第k距离局部可达密度的平均值
也就是说,点 p p p的局部离群因子 = = =点 p p p邻域点的密度的平均值比上点 p p p的密度
如果这个比值越接近1,说明 p p p与其邻域点密度差不多, p p p可能和邻域同属一簇;如果这个比值越小于1,说明 p p p的密度高于其邻域点密度, p p p为密集点;如果这个比值越大于1,说明 p p p的密度小于其邻域点密度, p p p越可能是异常点
python中LOF算法的使用
pip install -U scikit-learn
# 使用pip安装sklearn
from sklearn.neighbors import LocalOutlierFactor
clf = LocalOutlierFactor(n_neighbors=20, contamination=0.1)
# n_neighbors就是上面介绍中的k,第k邻域
# contamination是异常点在全部点中的比例
y_pred = clf.fit_predict(X)
# X是点的坐标,一个列表。每个元素又是一个列表,列表的两个数字元素,是点的坐标
# y_pred是预测的结果,1代表是inlier,-1代表是outlier
X_scores = clf.negative_outlier_factor_
# X_scores是计算的结果,都是负数,绝对值越大,越是outlier
结语
如果您有修改意见或问题,欢迎留言或者通过邮箱和我联系。
手打很辛苦,如果我的文章对您有帮助,转载请注明出处。