01.图论基础,图算法与图机器学习概况介绍
文章目录
- 课程简介
- 图的概念
-
- 图的重要性
- 常见图的应用分类
- 为什么要图+机器学习?
- 图表征
- 图相关基础概念
-
- 各种各样的图
- 图的表示方法
- 边的属性
- 图相关概念
- 重要的图属性
-
- 度分布
- 路径长度(距离)
- 聚集(群聚、集群)系数
- 连通分量
- 作业:分析维基百科选民网络
课程简介
课程网站就不贴了,以下是原课程介绍。后续将在这个专栏记录一些笔记和作业。
图诞生为一个简洁的数学概念:节点和节点之间关系的集合。如今图已经被广泛应用于建模许多真实世界的场景——从社交网络的人际关系,到信用卡的欺诈行为监测,再到遗传学与疾病检测,图无处不在。相比于其他的数据结构,图数据的一个重要的特性:图数据包含大量有价值的关系数据。然而,许多之前的机器学习模型往往只关注每个样本的特征,而没有考虑到样本之间的关系数据或没有很好的方法来利用和建模这些关系数据。图机器学习就应运而生了。近年来图逐渐变成机器学习的一个核心热门领域,拥有巨大的理论与实际应用发展前景。
本课程将结合图机器学习的数学理论基础与实际应用基础,深入浅出,来讲解当今最炙手可热的图机器学习与深度学习模型。从图论的数学基础开始,到经典的Google发家的PageRank搜索排名算法,到对利用节点本身特征和节点之间关系对节点进行分类的机器学习算法,再到诞生于近两年的图深度神经网络模型,本课程会为大家讲解模型的理论支持,模型结构,并讨论实际应用。学员在完成本课程之后,将拥有对图数据的深刻理解,与将在科研或工作中遇到的问题使用图机器学习的思路解决的能力。
参考教材
Networks, Crowds, and Markets: Reasoning about a Highly Connected World.
By David Easley and Jon Kleinberg. Cambridge University Press, 2010.
斯坦福的CS224W,18版:https://www.bilibili.com/video/av73701777,没有中字,凑合看吧
19版在这里:https://www.bilibili.com/video/BV1Vg4y1z7Nf?p=1,有中字
图的概念
“图"(Graph)与“网络"(Network)在文献中常互相通用,但有微小的区别网络常用于描述生活中实际存在的复杂系统,如社交网络等图是网络的数学表示方式
本课程中图=Graph,社交媒体研究领域中把图叫Network,本课程中二者混用不区分。()
数据结构中的图是顶点的有穷非空集合和顶点之间边的集合G(V,E)
下面看几个图数据的例子
社交网络:微博,微信,QQ
网页:不同网页之间的超链接
参考文献:文献的相互引用等
这里要说明的是,和数据结构一样,图也有分有向图和无向图,例如微博社交网络,A关注B,B不一定关注B,那么这里AB中间就是有向的关系;文献引用当然也是有向的。另外在网页和文献引用中可以从图的出入度来判断论文或者网页的重要性。
图的重要性
图定义了复杂系统中节点与节点之间的联系。为什么要研究这个玩意?
1.与传统的二维表不一样,关系型数据库通常是结构化数据,结构化数据适合存储那些表结构(属性)固定的信息,但是我们现实世界中万物各自属性不一样,很难用一个(或者有限个)表结构来进行存储
2.每个个体或者样本(可以看做数据库表中没一条记录),有的时候是有相互关系的,数据库中只能用主外键来表示表和表之间的关系,记录本身之间的关系无法表示(或者说表示得不彻底),例如表记录中记录了CPU,内存,主板等电子原件信息,但是某些CPU和主板是有配套关系的,这个关系就很难表达。
从数据历史发展来看,结构化数据实际上对真实世界进行了简化描述,早期图才是贴合数据描述的。
研究图=认识、建模、预测复杂系统的行为=直接对节点间的关系进行建模
常见图的应用分类
识别紧密联系的节点集群:社群识别(Community Detection)
所谓社群,是指图谱中共享相同的属性或承担相似角色的一组个体,社会关系中常见的社群例如家庭、同事圈、朋友圈等等。典型的社群识别应用有:
关系图谱中识别欺诈团伙(Fraud Detection)是一个典型应用。https://www.weiyangx.com/306008.html
可参考数量社会学。
社交网络中的意见分化:曾经有人用图来分析非死不可上发文情况来预测××结果。
预测某个节点的所属分类:对图的节点分类(Node Classification)
预测两个节点之间是否有关系:链结预测(Link Prediction)。典型应用为:知识推断。例如:基于规则:“爸爸的爸爸是爷爷”可以推理出谁是谁的爷爷。
还有推荐系统
计算生物学:多种药同时服用的副作用:使用GNN来对多种药物同时使用时产生的副作用进行建模
测量节点之间/网络之间的相似度:网络相似度(Network Similarity)。典型应用为:图可以做像高分子分类、3D视觉分类等任务。
为什么要图+机器学习?
不是为图数据而设计的机器学习方法往往只关注每个样本的特征,而没有考虑到样本之间的关系数据或没有很好的方法来利用和建模这些关系数据。
换句话说就是通常的算法考虑所有样本都来自同一分布,而实际上样本与样本可能是独立分布的。GML是来建模这种独立分布样本之间关系的方法。
图表征
这个玩意很重要,就类似Word2Vec一样。将图的节点映射到低维的向量,且拥有相似相邻结构的节点在嵌入空间中也更相近
https://zhuanlan.zhihu.com/p/62629465

图相关基础概念
基本和数据结构里面差不多,但是表达的意思不一样,具体可以参考数据结构(C++)笔记:06.图
| 现实 | 逻辑表达 | 数学表达 |
|---|---|---|
| 对象 | 节点 | N N N |
| 相互作用 | 边、链接 | E E E |
| 系统 | 网络、图 | G ( N , E ) G(N,E) G(N,E) |
从上表可知,建立一个图需要知道:节点和边是什么?(不同应用考虑的边(关系)不一样。)
表示一个图需要根据研究的问题来选择合适图的表示方法,这里注意,图的表示不一定唯一的,可能有多种表示方法。
节点的度,有向图中出度和入度。
各种各样的图
无向图:边是对称、相互的(没有方向),如QQ好友(其实QQ和微信好友不是相互的,可以拉黑),同学关系
有向图:边是有方向的,与一个节点相关联的边有出边和入边之分,与一个有向边关联的两个节点也有起点和终点之分,如微博的关注关系、汽车站点路径
完全图:节点两两之间都有一条边的无向图。无向图的边为:
E = N ( N − 1 ) 2 , N 为 节 点 数 目 E=\cfrac{N(N-1)}{2},N为节点数目 E=2N(N−1),N为节点数目
二分图:两个不相交的集合,可以看到边的两个端点分别在两个集合中,同一个集合中任意两个节点没有相邻关系。
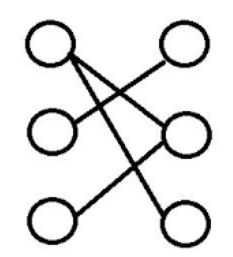
未加权图和加权图(每个又可以分为有向和无向)
自环图(又可以分为有向和无向):节点可以自己连接到自己。
多重图(又可以分为有向和无向):两个节点之间可以有多个边相连。
无环图和有环图(又可以分为有向和无向)
强连通有向图:有向图中每一个节点到另一个节点都有路径,反之亦然(相当于两个节点有两条边相连,或者节点有环)
弱连通有向图:忽略边的方向才连通的有向图
现实应用与图的对应:
邮件网络:有向,多重,允许节点与自己有链结(自己和自己发邮件)
微博好友网络:有向,可有/无权重(如沟通频率)
facebook好友网络:无向,可有/无权重(如沟通频率)
电话网络:有向,多重
图的表示方法
邻接矩阵,多为稀疏矩阵
边表,图以边的集合来表示图
邻接表
边的属性
边在不同应用中可以表示不同的含义:
权重(如:两个好友之间发消息的频率、路径的长短,引文的多少)
排名(如:最好的朋友,第二好的朋友…)
类型(同学,同事,亲戚,同班,同宿舍…)
图相关概念
节点的度,有向图中出度和入度。
路径:是一个顶点序列(这个是重点),使得从它的每个顶点有一条边到该序列中下一顶点。路径允许经过同一条边多次,例如:ABABAB是A到B的路径。
连通度
连通分量(无向图才有这个)
最大连通分量(无向图才有这个)
强连通分量(Strongly connected components (SCCs))(有向图才有这个)
重要的图属性
数据结构中很少关注下面这些属性:
度分布(Degree Distribution): P ( k ) P(k) P(k)
路径长度(Path Length): h h h
聚集(群聚、集群)系数(Clustering Coefficient): C C C
连通分量(Connected Components): s s s
度分布
度分布是对一个网络中节点度数的总体描述(就是度为1的节点占总节点数量的百分比、度为2的节点占总节点数量的百分比、度为3的节点占总节点数量的百分比…以此类推):
P ( k ) = N k N P(k)=\cfrac{N_k}{N} P(k)=NNk
N为节点数量
N k N_k Nk为度为k的节点的数量
路径长度(距离)
本来路径中允许经过同一条边多次,但是求路径长度的时候是指最短路径。例如:ABABAB是A到B的路径,但是路径长度 h A , B = 2 h_{A,B}=2 hA,B=2
最长的最短路径称为图的直径(Network Diameter): max ( h i , j ) , j ≠ i \text{max}(h_{i,j}),j\neq i max(hi,j),j=i
两点之间无路径,距离则为无穷大(或0).
有向图中两点的路径长度不一定相等 h A , B ≠ h B , A h_{A,B}\neq h_{B,A} hA,B=hB,A
连通图/强连通有向图/连通分量的平均路径长度:
h ˉ = 1 2 E m a x ∑ i , j ≠ i h i , j \bar h=\cfrac{1}{2E_{max}}\sum_{i,j\neq i}h_{i,j} hˉ=2Emax1i,j=i∑hi,j
其中:
h i , j h_{i,j} hi,j是从节点 i i i到节点 j j j的距离
E m a x = n ( n − 1 ) 2 E_{max}=\cfrac{n(n-1)}{2} Emax=2n(n−1)是最大的边的数量
聚集(群聚、集群)系数
节点 i i i的聚集系数 C i C_i Ci:描述节点 i i i的相邻节点之间结集成团的程度。
例如,生活社交网络中,你的朋友之间相互认识的程度;
网页、文献的重要程度。
C i = 2 e i k i ( k i − 1 ) , C i ∈ [ 0 , 1 ] C_i=\cfrac{2e_i}{k_i(k_i-1)},C_i\in[0,1] Ci=ki(ki−1)2ei,Ci∈[0,1]
e i e_i ei:是除当前节点 i i i外,其他 k i k_i ki个相邻节点之间的最大的边的数量。节点 i i i与相邻节点之间的边的数量。
k i k_i ki:表示当前节点 i i i有 k i k_i ki个相邻节点
完全图中的聚集系数等于1。
以下图例来自维基百科,注意看黑线是 e i e_i ei,灰线是 k i k_i ki。

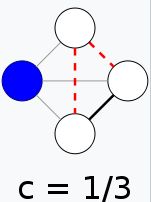
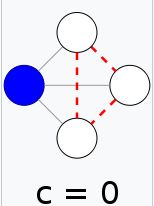
以上是无向图,有向图还要考虑方向。
算出一个图里的每一个顶点的聚集系数后,可以计算整个图的平均聚集系数。其实就是所有顶点的局部集聚系数的算术平均:
C = 1 N ∑ i N C i C=\cfrac{1}{N}\sum_i^NC_i C=N1i∑NCi
连通分量
查找连通分量的伪代码
从随机选择一个节点开始,进行宽度优先搜索(BFS)
记录BFS经过的所有节点
如果所有节点BFS都经过了,那么网络为连通图
否则从没被BFS经过的点开始,重复BFS
当然以上不是最优算法,具体可以看这里:
https://zhuanlan.zhihu.com/p/64916637
http://blog.sina.com.cn/s/blog_8d84b9240101f5e0.html
https://blog.csdn.net/hurmishine/article/details/75248876
作业:分析维基百科选民网络
参考:https://www.yuque.com/mamudechengxuyuan/kvkh16/wamgd3
数据集下载:http://snap.stanford.edu/data/wiki-Vote.html
介绍帖过来:
Wikipedia is a free encyclopedia written collaboratively by volunteers around the world. A small part of Wikipedia contributors are administrators, who are users with access to additional technical features that aid in maintenance. In order for a user to become an administrator a Request for adminship (RfA) is issued and the Wikipedia community via a public discussion or a vote decides who to promote to adminship. Using the latest complete dump of Wikipedia page edit history (from January 3 2008) we extracted all administrator elections and vote history data. This gave us 2,794 elections with 103,663 total votes and 7,066 users participating in the elections (either casting a vote or being voted on). Out of these 1,235 elections resulted in a successful promotion, while 1,559 elections did not result in the promotion. About half of the votes in the dataset are by existing admins, while the other half comes from ordinary Wikipedia users.
The network contains all the Wikipedia voting data from the inception of Wikipedia till January 2008. Nodes in the network represent wikipedia users and a directed edge from node i to node j represents that user i voted on user j.
看不懂没关系,下面是重点:
维基百科选民网络是一个有向图 G = ( V , E ) G=(V,E) G=(V,E),具有节点集 V V V和边集 E ∈ V × V E\in V×V E∈V×V,其中(边是节点的有序对)。边 ( a , b ) ∈ E (a,b)\in E (a,b)∈E表示用户a投票给用户b。
统计结果:
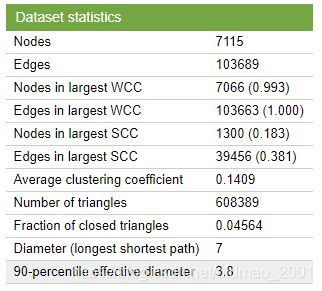
作业分两部分:
1、手工编程计算(不使用现成的包):
图中的节点数量
图中的有向边数量
图中的无向边数量,当两个节点都相互有指向,则这两个节点的边看做是无向边。
图中0出度的节点数量
图中0入度的节点数量
图中最大强连通分量的节点和边的数量
图中最大弱连通分量的节点和边的数量
图的平均聚集系数
# This is a sample Python script.
import os
# Press the green button in the gutter to run the script.
if __name__ == '__main__':
print(os.listdir('./data')) # 这里应该判断文件是否存在
startline = 3 # 从start开始读取
s = [] # 定义存放读取文件记录的list
StartNode = []
EndNode = []
TotalNode = []
with open("./data/wiki-Vote.txt", "r") as f:
for i in range(0, startline): # 忽略前面3行说明
f.readline()
for each in f:
G_array = each.strip() # 读取每一行数据
s.append(list(map(int, G_array.split("\t")))) # 将\t制表符为分隔符将两个节点分开,并转化为整形
for edge in s:
StartNode.append(edge[0]) # 读取起始点
EndNode.append(edge[1]) # 读取结束点
TotalNode = StartNode + EndNode # 合并节点
TotalNode = list(set(TotalNode)) # 去重得到节点数量
# 计算图中的无向边数量
countUndirEdge = 0
temprd = s # 设置临时记录集
for edge in temprd:
if ([edge[1], edge[0]] in temprd): # 找到相互指向的边,计数器加1,把该边移除,这里比较慢,可以换在节点list中查找会快
temprd.remove([edge[1], edge[0]])
countUndirEdge = countUndirEdge + 1
# #temprd.remove(edge) # 移除查找过的边
# 计算图中0出度的节点数量 法1
countOutputNode = 0
for outputNode in TotalNode:
if (outputNode not in StartNode):
countOutputNode = countOutputNode + 1
# 计算图中0出度的节点数量 法2
outNode = list(set(TotalNode) - set(StartNode))
# print("aaa",len(outNode))
# 计算图中0出度的节点数量 法1
countInputNode = 0
for inputNode in TotalNode:
if (inputNode not in EndNode):
countInputNode = countInputNode + 1
inNode = list(set(TotalNode) - set(EndNode))
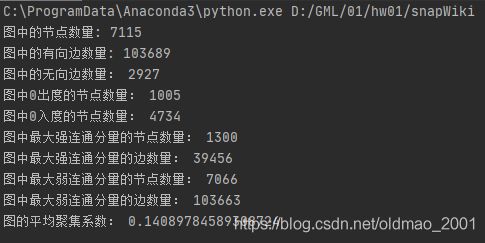
print('图中的节点数量:', len(TotalNode)) # 7115
print('图中的有向边数量:', len(s)) # 103689
print('图中的无向边数量:', countUndirEdge) # 2927
print('图中0出度的节点数量法1:', countOutputNode) # 1005
print('图中0入度的节点数量法1:', countInputNode) # 4734
print('图中0出度的节点数量法2:', len(outNode)) # 1005
print('图中0入度的节点数量法2:', len(inNode)) # 4734
# See PyCharm help at https://www.jetbrains.com/help/pycharm/
2、用SNAP计算以上参数。
https://blog.csdn.net/weixin_40493501/article/details/104471591
弄了半天,直接下载后解压放项目目录,
这里注意要使用3.7版本的python。。。不然报错到怀疑人生(DLL加载错误)。
代码可以参考官档
#import os
import snap#这个玩意要python3.7才不会报错
# Press the green button in the gutter to run the script.
if __name__ == '__main__':
G1 = snap.LoadEdgeList(snap.PNGraph, './data/wiki-Vote.txt', 0, 1)
MxScc = snap.GetMxScc(G1)# 图中最大强连通分量
MxWcc = snap.GetMxWcc(G1)# 图中最大弱连通分量
# for EI in MxScc.Edges():
# print("edge: (%d, %d)" % (EI.GetSrcNId(), EI.GetDstNId()))
print('图中的节点数量:', G1.GetNodes())# 7115
print('图中的有向边数量:', snap.CntUniqDirEdges(G1))# 103689
print('图中的无向边数量:', snap.CntUniqBiDirEdges(G1)) # 2927
print('图中0出度的节点数量:', snap.CntOutDegNodes(G1,0))# 1005
print('图中0入度的节点数量:', snap.CntInDegNodes(G1,0))#4734
print('图中最大强连通分量的节点数量:', MxScc.GetNodes())#1300
print('图中最大强连通分量的边数量:', snap.CntUniqDirEdges(MxScc))#39456
print('图中最大弱连通分量的节点数量:', MxWcc.GetNodes()) # 7066
print('图中最大弱连通分量的边数量:', snap.CntUniqDirEdges(MxWcc)) # 103663
print('图的平均聚集系数:',snap.GetClustCf (G1, -1))# # 0.14089784589308724