10. 基于近似的on-policy控制方法--阅读笔记【Reinforcement Learning An Introduction 2nd】

基于近似的on-policy控制方法

前言

本章将讲解控制问题，也就是如何找到一个优化策略。结合上一节参数化的方法，动作值函数的拟合函数$\hat{q}(s,a,\mathbf{w})\approx q_{\ast }(s,a)$,其中$\mathbf{w}\in {\mathbb{R}}^d$.目前我们主要采用on-policy的方法。并且本章将重点关注半梯度Sarsa算法，是基于上一节的半梯度TD(0)扩展而来的。对于episodic task来说，半梯度Sarsa是很自然的，但是对于continuing task来说，就需要回到折扣化的最优策略定义重新进行分析。本章先从episodic task入手，先将之前的关于状态值函数的近似延伸为动作值函数的近似；然后再探讨基于GPI模式和greedy的控制方法。把n-step 线性Sarsa在mountain car环境上进行测试，最后扩展到continuing task。

1. episodic半梯度控制

episodic半梯度Sarsa预测

首先将之前的半梯度预测方法扩展到动作值函数，这样才可以得到半梯度控制方法。主要有以下几个变化：估计目标发生变化 ，现在我们要估计的是$\hat{q}(s,a,w)$。之前对于值函数估计的样本形式是$S_t\mapsto U_t$，现在对于动作值函数估计的样本形式就变为了$S_t,A_t\mapsto U_t$。这里的$U_t$可以是任意一种对于$q_{\pi }(S_t,A_t)$的近似。比如MC的回报$G_t$，或者是n-step Sarsa。
$$G_{t:t+n}\doteq R_{t+1}+\gamma R_{t+2}+...+{\gamma }^{n-1}{R}_{t+n}+{\gamma }^n{q}_{t+n-1}(S_{t+n},A_{t+n},w_t),n\ge 1,0\le t<T-n$$
所以基于半梯度的权重更新公式为
$${\mathbf{w}}_{t+1}\doteq {\mathbf{w}}_t+\alpha \left[U_t-\hat{q}\left(S_t,A_t,{\mathbf{w}}_t\right)\right]\nabla \hat{q}\left(S_t,A_t,{\mathbf{w}}_t\right)$$
当更新方式采用的是one-step Sarsa时，更新公式就可以写作：
$${\mathbf{w}}_{t+1}\doteq {\mathbf{w}}_t+\alpha \left[R_{t+1}+\gamma \hat{q}\left(S_{t+1},A_{t+1},{\mathbf{w}}_t\right)-\hat{q}\left(S_t,A_t,{\mathbf{w}}_t\right)\right]\nabla \hat{q}\left(S_t,A_t,{\mathbf{w}}_t\right)$$
这个式子对应的算法就叫做episodic 半梯度单步sarsa算法。对于一个固定的策略来讲，该算法可以保证要估计的动作值函数渐进收敛到真实的动作值函数。

episodic半梯度Sarsa控制
按照传统的GPI的思路，在得到动作值函数的预测之后再配合一定的策略提升，就可以逐渐收敛到一个最优策略上。但是对于连续动作空间或者很大的离散动作空间来讲，目前还没有有效的技术可以进行动作选择。对于离散的不太大的动作空间，可以借助之前的方法计算出每个动作的$\hat{q}(S_t,a,W_t)$，然后再通过贪婪策略选择值最大的对应的动作即可。

example:mountain car
任务描述：让一个动力不足的小车按照一定策略越过山顶某个goal。看下图所示。
因为动力不足，所以小车必须先向左边开，积累一定的势能之后再加上自身现有的动力才能到达目标点。小车到达goal则episode结束，如果超过左边的边界就重置task。
状态空间：二维连续空间。-1.2≤$x_{t+1}$≤0.5，-0.07≤$v_{t+1}$≤0.07，位置和速度两个变量
动作空间：+1，-1, 0。分别表示正向马力全开，逆向马力全开，关闭引擎
模型：状态转移方程：
$$\begin{array}{l}{x}_{t+1}\doteq \text{bound}\left[x_t+{\dot{x}}_{t+1}\right]\\ {\dot{x}}_{t+1}\doteq \text{bound}\left[{\dot{x}}_t+0.001A_t-0.0025\cos \left(3x_t\right)\right]\end{array}$$
回报： -1/step

线性近似 ：采用线性近似器来表示动作值函数。
$$\hat{q}(s,a,\mathbf{w})\doteq {\mathbf{w}}^{\top }\mathbf{x}(s,a)=\sum _{i=1}^d{w}_i\cdot x_i(s,a)$$
其中x(s,a)是特征向量，借助上一章中提到的任意一种特征构造方法均可。这里采用tile-coding的方法，把连续状态编码为二值特征。
构造堆编码特征 ：采用8个tilings，每个tiling有64个tile，tiling之间采用非对称偏移方式。对于每个状态来说就是一个8维的表征向量。这个8维向量中的每个值就是每个tiling中落在对应状态上的tile的地址/索引。因为要返回索引，所以一般采用哈希表存储。具体关于堆编码的使用，查看：http://incompleteideas.net/tiles/tiles3.html
学习的目标函数是值函数的负数（因为一般的提供的都是梯度下降法，要求一个最小值，如果值函数的负数最小那就意味着值函数本身最大）

2.半梯度n-step sarsa

上一节中我们提到了半梯度单步sarsa预测方法，实际上就是通过单步自举来估计$U_t$，那么对于n-step sarsa来说就是自举到n步。
$$G_{t:t+n}\doteq R_{t+1}+\gamma R_{t+2}+\cdots +{\gamma }^{n-1}{R}_{t+n}+{\gamma }^n\hat{q}\left(S_{t+n},A_{t+n},{\mathbf{w}}_{t+n-1}\right),t+n<T$$
当t+n＞T时，$G_{t:t+n}$就等价于MC的计算方式。
因此对于半梯度n-step Sarsa预测方法来讲，就是用上式计算$G_{t:t+n}$代替之前的$U_t$即可。
$${\mathbf{w}}_{t+n}\doteq {\mathbf{w}}_{t+n-1}+\alpha \left[G_{t:t+n}-\hat{q}\left(S_t,A_t,{\mathbf{w}}_{t+n-1}\right)\right]\nabla \hat{q}\left(S_t,A_t,{\mathbf{w}}_{t+n-1}\right),0\le t<T$$

基本的计算流程与上一节一样，只是计算$U_t$的方式变了。同时，这个流程与第七章中表格型的计算方法也完全一样，仅仅是把查表转换成了计算线性近似器$\hat{q}(S,A,w_t)$
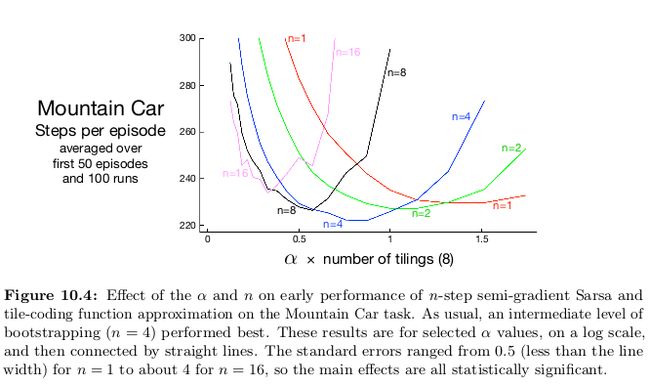
比较n=1和n=8时算法的学习速度：

3.平均奖励：针对连续任务的一种新的回报形式

对于continuing task来说，在采用值函数近似的方法中需要定义一种新的值函数----平均回报，平均回报是没有折扣因子的，所以所有后续回报对当前状态的值都有等价值的影响作用。下一节我们会讨论为什么折扣的累积回报在带有拟合器的方法中是不合适的，平均回报则表现不错。
平均回报
定义如下：
$$\begin{array}{rlrl}r(\pi )& \doteq \underset{h\to \infty }{\lim }\frac{1}{h}\sum _{t=1}^h\mathbb{E}\left[R_t|S_0,A_{0:t-1}\sim \pi \right]& & \\ & =\underset{t\to \infty }{\lim }\mathbb{E}\left[R_t|S_0,A_{0:t-1}\sim \pi \right]& & \\ & =\sum _s{\mu }_{\pi }(s)\sum _a\pi (a|s)\sum _{s^{\prime },r}p\left(s^{\prime },r|s,a\right)r& & \end{array}$$
其中${\mu }_{\pi }(s)\doteq {\lim }_{t\to \infty }Pr\left\{S_t=s|A_{0:t-1}\sim \pi \right\}$表示的是状态的稳态分布。假设这个分布一定存在，且和初始状态S0无关，这一特性在MDP中叫做各态遍历性。其含义就是无论MDP从哪个状态开始或者agent早期采取什么样的决策，仅仅只会产生瞬时的影响，长远来看，处于某个状态的概率只与策略和转移概率有关。
能够使得上式$r(\pi )$最大化的策略就是最优策略。${\mu }_{\pi }(s)$叫做稳态分布的含义就是，无论在policy下采取什么样的action或者状态之间如何进行转移，最终状态的分布依然不变:
$$\sum _s{\mu }_{\pi }(s)\sum _a\pi (a|s)p\left(s^{\prime }|s,a\right)={\mu }_{\pi }\left(s^{\prime }\right)$$

微分值函数
有了上述平均回报的定义，根据这个回报定义一个continuing task对应的新的回报，表示为每步立即回报的值与平均回报之间的差值的和：
$$G_t\doteq R_{t+1}-r(\pi )+R_{t+2}-r(\pi )+R_{t+3}-r(\pi )+\cdots$$
这个回报叫做微分/差分回报 ，对应的值函数叫做微分/差分值函数 。其状态值函数和动作值函数的表示为：
$$\begin{gathered} v_{\pi }(s)\doteq {\mathbb{E}}_{\pi }\left[G_t|S_t=s\right] \\ {q}_{\pi }(s,a)\doteq {\mathbb{E}}_{\pi }\left[G_t|S_t=s,A_t=a\right] \end{gathered}$$
微分值函数对应的贝尔曼方程和最优贝尔曼方程为 ：
$$\begin{array}{l}{v}_{\pi }(s)={\sum }_a\pi (a|s){\sum }_{r,s^{\prime }}p\left(s^{\prime },r|s,a\right)\left[r-r(\pi )+v_{\pi }\left(s^{\prime }\right)\right]\\ q_{\pi }(s,a)={\sum }_{r,s^{\prime }}p\left(s^{\prime },r|s,a\right)\left[r-r(\pi )+{\sum }_{a^{\prime }}\pi \left(a^{\prime }|s^{\prime }\right)q_{\pi }\left(s^{\prime },a^{\prime }\right)\right]\\ v_{\ast }(s)={\max }_a{\sum }_{r,s^{\prime }}p\left(s^{\prime },r|s,a\right)\left[r-{\max }_{\pi }r(\pi )+v_{\ast }\left(s^{\prime }\right)\right],\\ q_{\ast }(s,a)={\sum }_{r,s^{\prime }}p\left(s^{\prime },r|s,a\right)\left[r-{\max }_{\pi }r(\pi )+{\max }_{a^{\prime }}{q}_{\ast }\left(s^{\prime },a^{\prime }\right)\right]\end{array}$$
这里没有了折扣系数并且r也发生了变化。
对应微分形式的TD error可以表示为：
$$\begin{gathered} {\delta }_t\doteq R_{t+1}-{\overline{R}}_t+\hat{v}\left(S_{t+1},{\mathbf{w}}_t\right)-\hat{v}\left(S_t,{\mathbf{w}}_t\right) \\ {\delta }_t\doteq R_{t+1}-{\overline{R}}_t+\hat{q}\left(S_{t+1},A_{t+1},{\mathbf{w}}_t\right)-\hat{q}\left(S_t,A_t,{\mathbf{w}}_t\right) \end{gathered}$$
其中${\overline{R}}_t$是t时刻的平均回报$r(\pi )$。结合上面的定义，之前所讲过的所有算法和结论都可以适用于平均回报的情况，例如微分形式的半梯度sarsa算法只需要把${\mathbf{w}}_{t+1}\doteq {\mathbf{w}}_t+\alpha {\delta }_t\nabla \hat{q}\left(S_t,A_t,{\mathbf{w}}_t\right)$中的${\delta }_t$换成对应的微分形式的求解方式即可。
微分形式的半梯度sarsa预测方法伪代码：（注意${\overline{R}}_t$的求解过程）

example:
来自：https://blog.csdn.net/u013695457/article/details/91353072

4.弃用折扣设置deprecating the discounting setting

对于基于表格的问题，之前介绍的折扣方法会取得较好的结果，但是对于采用近似拟合器的情况这种办法就会有一些问题。
假设对于一个没有始终的无穷序列，那么没有明确定义的状态，状态只能用特征向量来表示，假设特征向量不变。我们需要利用回报序列和动作序列来评价策略的好坏。由于没有明确定义的状态，所以无法给出每个状态的值。那么我们可以计算从当前时刻起很长区间的折扣累积回报，但是不同时间的累积折扣汇报不同，所以可以算不同时刻的累积回报的均值，以此作为序列好坏的衡量标准。最终得到的结果实际上是$r(\pi )/(1-\gamma )$，折扣因子实际上没有任何意义。
证明：
$$\begin{array}{rlr}J(\pi )& =\sum _s{\mu }_{\pi }(s)v_{\pi }^{\gamma }(s)& \text{ (其中 }{v}_{\pi }^{\gamma }\text{ 是折扣价值函数) }\\ & =\sum _s{\mu }_{\pi }(s)\sum _a\pi (a|s)\sum _{s^{\prime }}\sum _{r}p\left(s^{\prime },r|s,a\right)\left[r+\gamma v_{\pi }^{\gamma }\left(s^{\prime }\right)\right]& \text{(Bellman 方程)}\\ & =r(\pi )+\sum _s{\mu }_{\pi }(s)\sum _a\pi (a|s)\sum _{s^{\prime }}\sum _{r}p\left(s^{\prime },r|s,a\right)\gamma v_{\pi }^{\gamma }\left(s^{\prime }\right)& \\ & =r(\pi )+\gamma \sum _{s^{\prime }}{v}_{\pi }^{\gamma }\left(s^{\prime }\right)\sum _s{\mu }_{\pi }(s)\sum _a\pi (a|s)p\left(s^{\prime }|s,a\right)& \\ & =r(\pi )+\gamma \sum _{s^{\prime }}{v}_{\pi }^{\gamma }\left(s^{\prime }\right){\mu }_{\pi }\left(s^{\prime }\right)& \\ & =r(\pi )+\gamma J(\pi )& \\ & =r(\pi )+\gamma r(\pi )+{\gamma }^{2}J(\pi )& \\ & =r(\pi )+\gamma r(\pi )+{\gamma }^{2}r(\pi )+{\gamma }^{3}r(\pi )+\cdots & \\ & =\frac{1}{1-\gamma }r(\pi )& \end{array}$$
对于近似的方法，我们计算的是value error关于参数的导数，也就是说我们关注的是策略整体性能的好坏，并不是所有状态值函数的加权均值。所以折扣因子并不影响策略的相对好坏，对于连续任务来说，使用平均回报就可以取得很好的效果。但是我们最初基于表格化的方法是针对每个状态下的策略单独进行考虑的，不同策略之间并不会相互影响，因此不必看成一个整体。所以可以使用折扣值函数定义。
从理论上分析，是因为近似拟合器的引入导致了策略提升理论失效。所以对于单个状态值函数的提升就无法导致整体策略提升。因为单个状态值函数的变化在近似拟合器上会影响其他状态。
实际上，对于episodic task，使用平均回报依然无法保证策略有所提升。因为拟合器类方法在理论上没有保证。后续会介绍策略梯度理论，该理论类似与策略提升，在该理论下可以保证策略有所改善。

5. 微分半梯度n-step sarsa算法

之前的内容我们介绍了半梯度n-step sarsa算法以及微分回报形式，本节介绍的微分半梯度sarsa算法实际上就是把之前半梯度n-step sarsa算法中计算回报$G_t$的方式改为微分回报形式即可。
$$G_{t:t+n}\doteq R_{t+1}-{\overline{R}}_{t+n-1}+\cdots +R_{t+n}-{\overline{R}}_{t+n-1}+\hat{q}\left(S_{t+n},A_{t+n},{\mathbf{w}}_{t+n-1}\right)$$
注意这里的$\overline{R}$是需要进行估计的。完整的TD error表达式为：
$${\delta }_t\doteq G_{t:t+n}-\hat{q}\left(S_t,A_t,\mathbf{w}\right)$$
算法的伪代码如下：注意计算$\overline{R}$的方式：

核心步骤就是：求微分形式的TD error；更新平均回报的估计；沿梯度方向更新权重

总结

本章主要在第九章的基础上介绍了如何使用半梯度方法求策略。对于episodic task来说直接采用GPI模式扩展即可。对于continuing task来说，引入了一个新的问题形式化方法，平均回报 ，通过比较平均回报来评价策略的好坏。基于这个平均回报，定义了一种新的回报形式，微分回报以及对应的微分值函数、贝尔曼方程等等。