13. 策略梯度方法--阅读笔记【Reinforcement Learning An Introduction 2nd】

策略梯度方法

前言

之前我们所讲的方法都是基于值函数的，基本的流程就是先求出值函数的值，然后再根据值函数值的大小选择一个动作。这类方法叫做action-value methods。我们的目的是找到一个策略，事实上没有必要求解值函数，可以直接参数化一个策略，然后通过更新参数来优化策略即可。把这种不依赖于值函数，而是直接优化一个参数化策略的学习方法叫做基于策略的方法。这类方法有时候也会计算值函数，比如基于actior-critic架构的方法，但是此时值函数不用来决策只用来评估，所以依然是基于策略的方法。
把来自于策略的参数用$\theta \in {\mathbb{R}}^{d^{\prime }}$,对应的策略表示为$\pi (a|s,\theta )=Pr(A_t=a|S_t=s,{\theta }_t=\theta )$,而值函数的参数表示方法与之前的一致，$w\in {\mathbb{R}}^d$.

策略梯度方法
基于策略搜索的方法很多，比如交叉熵搜索，自然梯度法等等，本章介绍最常用的策略梯度法。策略梯度是通过某个参数化性能指标$J(\theta )$的梯度来更新策略参数。 为了最大化性能，参数的更新应该是梯度上升的，即：
$${\theta }_{t+1}={\theta }_t+\alpha \nabla J\left({\theta }_t\right)$$
$J\left({\theta }_t\right)\in {\mathbb{R}}^{d^{\prime }}$是一个随机估计，是由样本得到的随机向量。形如这一类的方法叫做策略梯度方法。如果一个方法既学习策略又学习值函数，那么就叫做actor-critic方法，actor就是要学习的策略，用来产生动作，critic就是用来学习值函数，一般是状态值函数，用来反映某个状态的好坏。

1. 策略近似及其优势

在策略梯度方法中，策略可以被参数化为任何形式，只要$\pi (a|s,\theta )$相对于参数θ是可微的即可。即$\nabla \pi (a|s,\theta )$对于任何的s∈S，a∈A(s)都是存在的。策略也分为确定性策略和随机策略，为了保证探索通常需要随机策略。$\pi (a|s,\theta )\in (0,1)$,本节介绍最常用的对于离散动作空间的策略参数化形式，并且给出策略梯度方法相对于动作值函数方法的优势，策略梯度方法一个重要的特点在于其能解决连续动作空间的问题。

如果动作空间是离散的并且规模不大，一个简单的参数化技巧就是定义一个带参数的偏好函数h(s,a,θ)∈R，动作的偏好越高被选择的概率越大。比如可以定义一个指数soft-max分布：
$$\pi (a\mid s,\mathbf{\theta })\doteq \frac{e^{h(s,a,\mathbf{\theta })}}{{\sum }_b{e}^{h(s,b,\mathbf{\theta })}}$$
这种策略的参数化方式叫做动作偏好soft-max，动作偏好自身的参数化方式是任意的，可以是一个神经网络，θ是网络的权重参数，也可以是特征向量的线性函数。
$$h(s,a,\mathbf{\theta })={\mathbf{\theta }}^{\top }\mathbf{x}(s,a)$$
参数化策略的优势之一在于通过定义的softmax操作可以使策略趋向于一个确定性策略。（对于动作偏好求指数那么就会放大这种偏好，对于偏好值小的动作概率也就小了。）但是如果基于动作值的softmax来求测了，这个策略一般无法趋向于一个确定性策略。
参数化策略的第二个优势在于可以以任意的概率选择动作，从而可以近似任意的随机最优策略。动作值方法本质上没有这样的特性。
选择参数化策略的一个原因还有就是，可以通过特定的策略参数化形式注入一些先验知识，从而快速的学习到有用的策略。

2.策略梯度理论

策略参数化相比于值函数选择动作除了具有实际的优势以外，还有理论上的优势，策略梯度理论。对于值函数而言，状态值的微小变化，就有可能产生完全不同的策略，但是对于策略梯度方法而言，由于策略函数是可微的，所以产生的变化也是平滑稳定的。

对于episodic task和continuing task而言，性能指标$J(\theta )$的形式不同，所以对应的策略梯度的推导过程也不同。本节先介绍episodic task的情况。性能指标定义为状态的值。假设每个episode的起始状态为$s_0$，那么性能指标就可以定义为：
$J(\theta )\doteq v_{{\pi }_{\theta }}(s_0)$
策略梯度理论
有了函数近似，如何更新策略函数使得更新后的策略一定比之前好，这是一个挑战。一方面，策略的参数不仅会影响动作的选择，同时还会影响状态的分布。首先策略本身就是为了选择动作，自然会影响动作的选择。其次，状态的分布和环境因素比如转移概率等有关，而环境因素往往是未知的，也就是说梯度的更新会依赖于某些未知的因素。
不过策略梯度理论证明了性能指标关于策略参数的导数具有解析解，其推导过程并不涉及状态分布。策略梯度理论的结论如下：
$$\nabla J(\mathbf{\theta })\propto \sum _{\ast }\mu (s)\sum _a{q}_{\pi }(s,a)\nabla \pi (a\mid s,\mathbf{\theta })$$
梯度是个列向量，每个分量是参数θ对应分量的偏微分，梯度向量和右边部分成比例关系，对于episodic task来说，这个正比关系系数是episode的平均长度，对于continuing task来说，正比关系系数是1，$\mu$是on-policy分布。
策略梯度理论证明
为了简洁，证明过程中所有的$\pi$都是参数θ的函数，并且求导也是针对于变量θ的。首先把状态值函数写成动作值函数的形式：
$$\begin{gathered} \begin{array}{r}\nabla v_{\pi }(s)=\nabla \left[\sum _a\pi (a\mid s)q_{\pi }(s,a)\right],foralls\in \mathcal{S}\end{array} \\ =\sum _a\left[\nabla \pi (a\mid s)q_{\pi }(s,a)+\pi (a\mid s)\nabla q_{\pi }(s,a)\right](productruleofcalculus) \\ =\sum _a\left[\nabla \pi (a\mid s)q_{\pi }(s,a)+\pi (a\mid s)\nabla \sum _{s^{\prime },r}p\left(s^{\prime },r\mid s,a\right)\left(r+v_{\pi }\left(s^{\prime }\right)\right)\right] \\ =\sum _a\left[\nabla \pi (a\mid s)q_{\pi }(s,a)+\pi (a\mid s)\sum _{s^{\prime }}p\left(s^{\prime }\mid s,a\right)\nabla v_{\pi }\left(s^{\prime }\right)\right] \\ =\sum _a[\nabla \pi (a\mid s)q_{\pi }(s,a)+\pi (a\mid s)\sum _{s^{\prime }}p\left(s^{\prime }\mid s,a\right)\text{ (unrooling) } \\ \sum _{a^{\prime }}\left[\nabla \pi \left(a^{\prime }\mid s^{\prime }\right)q_{\pi }\left(s^{\prime },a^{\prime }\right)+\pi \left(a^{\prime }\mid s^{\prime }\right)\sum _{s^{\prime \prime }}p\left(s^{\prime \prime }\mid s^{\prime },a^{\prime }\right)\nabla v_{\pi }\left(s^{\prime \prime }\right)\right]] \\ =\sum _{x\in S}\sum _{k=0}^{\infty }\mathrm{Pr}(s\to x,k,\pi )\sum _a\nabla \pi (a\mid x)q_{\pi }(x,a) \end{gathered}$$
$\mathrm{Pr}(s\to x,k,\pi )$表示的是从状态s经历k步转移到状态x的概率。之前第九章中讲到$\eta (s)$表示的是在状态s的逗留时间，其实也就是这个状态被访问的概率，所以有：
$$\begin{array}{rl}\nabla J(\mathbf{\theta })& =\nabla v_{\pi }\left(s_0\right)\\ & =\sum _s\left(\sum _{k=0}^{\infty }\mathrm{Pr}\left(s_0\to s,k,\pi \right)\right)\sum _a\nabla \pi (a\mid s)q_{\pi }(s,a)\\ & =\sum _s\eta (s)\sum _a\nabla \pi (a\mid s)q_{\pi }(s,a)\\ & =\sum _{s^{\prime }}\eta \left(s^{\prime }\right)\sum _s\frac{\eta (s)}{{\sum }_{s^{\prime }}\eta \left(s^{\prime }\right)}\sum _a\nabla \pi (a\mid s)q_{\pi }(s,a)\\ & =\sum _{s^{\prime }}\eta \left(s^{\prime }\right)\sum _s\mu (s)\sum _a\nabla \pi (a\mid s)q_{\pi }(s,a)\\ & \propto \sum _s\mu (s)\sum _a\nabla \pi (a\mid s)q_{\pi }(s,a)\end{array}$$

其中用到了定义$\mu (s)=\frac{\eta (s)}{{\sum }_{s^{\prime }}\eta \left(s^{\prime }\right)}$,归一化的$\eta (s)$就是on-policy 分布。
重写上述策略梯度理论可得 ：
$$\begin{array}{rl}{\nabla }_{\theta }J(\theta )& \propto \sum _{s\in \mathcal{S}}{\mu }^{\pi }(s)\sum _{a\in \mathcal{A}}{q}^{\pi }(s,a){\nabla }_{\theta }{\pi }_{\theta }(a\mid s)\\ & =\sum _{s\in \mathcal{S}}{\mu }^{\pi }(s)\sum _{a\in \mathcal{A}}{\pi }_{\theta }(a\mid s)q^{\pi }(s,a)\frac{{\nabla }_{\theta }{\pi }_{\theta }(a\mid s)}{{\pi }_{\theta }(a\mid s)}\text{( Log-probability trick) }\\ & ={\mathbb{E}}_{\pi }\left[q^{\pi }(s,a){\nabla }_{\theta }\ln {\pi }_{\theta }(a\mid s)\right]\end{array}$$
经过log-probability trick，我们可以把策略梯度理论写成期望的形式，这样就可以通过采样来近似。在很多论文中都会看到策略梯度理论的期望形式的估计量。策略梯度理论也是很多其他策略梯度算法的理论基础。

3. REINFORCE：MC策略梯度

本节我们介绍REINFORCE策略梯度算法 。策略梯度的思想就是通过计算参数化的评价指标的梯度来更新策略参数，使用随机梯度上升法（SGA）更新策略参数，进而不断的最大化评价指标。核心问题是如何估计梯度，既然要估计，首先就应该采样样本，通过一种采样方式，使得采样样本估计的梯度期望正比于真实梯度。为何只需要正比于真实梯度即可？因为在梯度上升的计算式中有一个步长因子，也就是说，即使采样梯度是真实梯度的很多倍，那么通过调节这个步长因子也可以实现缩放的功用。只要控制好步长因子，采样梯度的精确值就不重要，因此只需要成正比即可。
策略梯度表明：
$$\begin{array}{rl}{\nabla }_{\theta }J(\theta )& \propto \sum _{s\in \mathcal{S}}{\mu }^{\pi }(s)\sum _{a\in \mathcal{A}}{q}^{\pi }(s,a){\nabla }_{\theta }{\pi }_{\theta }(a\mid s)\\ & ={\mathbb{E}}_{s\pi }\left[\sum _a{q}^{\pi }(S_t,a)\nabla \pi (a\mid S_t,\theta )\right]\end{array}$$
根据上式把对状态s求和的操作换做为求期望的操作，此时就得到了一个需要采样的量，其期望等于真实的梯度。这个采样值就是${\sum }_a{q}^{\pi }(S_t,a)\nabla \pi (a\mid S_t,\theta )$,按照梯度上升就可以构造如下算法：
$${\theta }_{t+1}\doteq {\theta }_t+\alpha \sum _a\hat{q}(S_t,a,w)\nabla \pi (a\mid S_t,\theta )$$
其中$\hat{q}$是$q_{\pi }$的估计值。上述方法叫做all-actions方法，因为在梯度更新中考虑了所有的动作。一般经典的REINFORCE算法在每个更新中只考虑一个实际采取的动作。就是把动作求和也变为求期望即可。
$$\begin{array}{rl}\nabla J(\mathbf{\theta })& ={\mathbb{E}}_{\pi }\left[\sum _a\pi \left(a\mid S_t,\mathbf{\theta }\right)q_{\pi }\left(S_t,a\right)\frac{\nabla \pi \left(a\mid S_t,\mathbf{\theta }\right)}{\pi \left(a\mid S_t,\mathbf{\theta }\right)}\right]\\ & ={\mathbb{E}}_{\pi }\left[q_{\pi }\left(S_t,A_t\right)\frac{\nabla \pi \left(A_t\mid S_t,\mathbf{\theta }\right)}{\pi \left(A_t\mid S_t,\mathbf{\theta }\right)}\right]\\ & ={\mathbb{E}}_{\pi }\left[G_t\frac{\nabla \pi \left(A_t\mid S_t,\mathbf{\theta }\right)}{\pi \left(A_t\mid S_t,\mathbf{\theta }\right)}\right]\end{array}$$
有了上述这个形式就可以得到SGA的另一个更新表达式如下：
$${\mathbf{\theta }}_{t+1}\doteq {\mathbf{\theta }}_t+\alpha G_t\frac{\nabla \pi \left(A_t\mid S_t,{\mathbf{\theta }}_t\right)}{\pi \left(A_t\mid S_t,{\mathbf{\theta }}_t\right)}$$
这就是REINFORCE算法 。
借助$\nabla lnx=\frac{\nabla x}{x}$将上式改写为：
$${\mathbf{\theta }}_{t+1}\doteq {\mathbf{\theta }}_t+\alpha G_t\nabla ln\pi (A_t|S_t,{\theta }_t)$$
如果$G_t$大于0，参数更新的方向会增加它在当前状态的概率，也就是说如果回报是有利的就增加这个动作出现的概率，并且回报越大，梯度更新的幅度也就越大，概率增加的也就越大。上述式子我们利用${\mathbb{E}}_{\pi }[G_t|S_t,A_t]=q_{\pi }(S_t,A_t)$把q换成了$G_t$,表示的是t时刻后的回报总和，通过MC方法计算得到。所以REINFORCE算法是基于MC的算法。
算法伪代码：

注意，在伪代码中更新参数时我们引入了折扣因子γ，这是为了兼容非episodic task。对于episodic task，其折扣因子γ等于1。（之前的公式推导中之所以没有这个折扣因子是因为我们默认按照1来计算）
REINFORCE算法可以保证收敛到局部最优，由于依赖于MC方法，所以其采样梯度是无偏估计，但是会导致方差大，降低学习效率。

4. 有baseline的REINFORCE算法

策略梯度理论定义为：
$$\nabla J(\mathbf{\theta })\propto \sum _{\ast }\mu (s)\sum _a{q}_{\pi }(s,a)\nabla \pi (a\mid s,\mathbf{\theta })$$
如果我们在上式的基础上给$q_{\pi }(s,a)$减去一个任意的基准线b(s)，那么结论依然成立。
$$\nabla J(\mathbf{\theta })\propto \sum _{\ast }\mu (s)\sum _a(q_{\pi }(s,a)-b(s))\nabla \pi (a\mid s,\mathbf{\theta })$$
该基准线b(s)可以是任意的函数，或者是随机变量，只要不依赖于a就可以。证明如下：
$$\sum _{a}b(s)\nabla \pi (a\mid s,\mathbf{\theta })=b(s)\nabla \sum _a\pi (a\mid s,\mathbf{\theta })=b(s)\nabla 1=0$$
因此我们就可以得到一个新的更新规则，就是带有baseline的REINFORCE算法，参数更新如下：
$${\mathbf{\theta }}_{t+1}\doteq {\mathbf{\theta }}_t+\alpha (G_t-b(s))\frac{\nabla \pi \left(A_t\mid S_t,{\mathbf{\theta }}_t\right)}{\pi \left(A_t\mid S_t,{\mathbf{\theta }}_t\right)}$$
实际上减去一个baseline并不会改变更新值得期望值，但是会影响其方差。
对于MDP问题来说，baseline依赖于状态，对于某些状态都具有比较大的动作值函数，那么就需要有一个大的baseline区分更大的动作值和相对小的动作值。但是对于其他一些状态，所有状态得值函数都比较小，那么就需要一个小的baseline。那么baseline value？ 可以使用估计的状态值函数来当作baseline，$b(s)=\hat{v}(S_t,w)$，仅仅依赖于状态。由于REINFORCE算法是基于MC的，所以可以使用MC来学习这个值函数。
带有baseline的REINFORCE算法伪代码：

主要过程：

• 计算MC回报，一是用来估计近似值函数，二是用来计算算法中的梯度
• 更新近似值函数中的参数w，基于MC的半梯度方法更新近似值函数的参数w
• 更新带有baseline的REINFORCE算法策略的参数θ

算法中有两个步长参数分别是${\alpha }^{\theta }$和${\alpha }^w$,第二个是值函数参数更新步长，根据之前所讲的内容，有一定的规则可以选择；第一个参数是策略参数的更新步长。

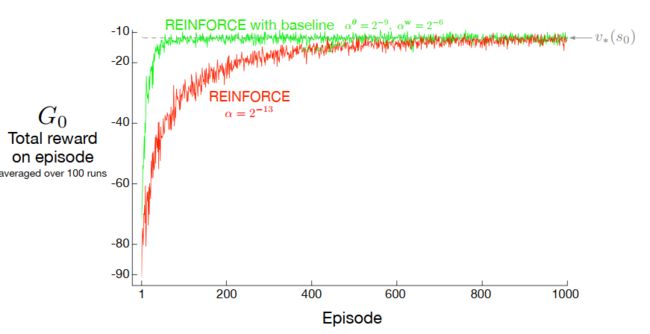
有baseline的效果明显要好一些，并且波动较无baseline算法的波动要小。

5. Actor-Critic方法

上述带有基准的REINFORCE算法虽然也引入了值函数，但是这个值函数的值仅仅是作为baseline，回报也是基于MC定义的。即使加入baseline可以减小算法的方差，但是MC依然不适用于连续任务。通过引入TD方法可以解决这些问题，将TD方法引入到策略梯度当中去就形成了Actor-Critic方法。
最简单的TD方法就是one-step TD方法，比如TD(0),Sarsa(0)等等。单步TD方法有两个优势：一是完全在线而是避免了引入资格迹。
把之前策略参数更新算式中的MC回报替换成单步TD目标即可：
$$\begin{array}{rl}{\mathbf{\theta }}_{t+1}& \doteq {\mathbf{\theta }}_t+\alpha (G_{t:t+1}-\hat{v}(S_t,w))\frac{\nabla \pi \left(A_t\mid S_t,{\mathbf{\theta }}_t\right)}{\pi \left(A_t\mid S_t,{\mathbf{\theta }}_t\right)}\\ & ={\mathbf{\theta }}_t+\alpha (R_{t+1}+\gamma \hat{v}(S_{t+1},w)-\hat{v}(S_t,w))\frac{\nabla \pi \left(A_t\mid S_t,{\mathbf{\theta }}_t\right)}{\pi \left(A_t\mid S_t,{\mathbf{\theta }}_t\right)}\\ & ={\mathbf{\theta }}_t+\alpha {\delta }_t\frac{\nabla \pi \left(A_t\mid S_t,{\mathbf{\theta }}_t\right)}{\pi \left(A_t\mid S_t,{\mathbf{\theta }}_t\right)}\end{array}$$

这里借助半梯度TD(0)方法学习critic。将这个算法扩展到n-step和λ-return也很直观，只需要将单步回报换成$G_{t:t+n}$和$G_t^{\lambda }$即可。这是从forward view的观点来看，从backward view的观点来看，就相当于是引入资格迹的形式。
对actor和cirtic分别使用资格迹即可。

6. 连续问题的策略梯度

对于continuing task和episodic task来说，性能指标函数是不太一样的。对于continuing task是没有终止状态的，因此如果计算累积回报和是不收敛的。在第10章中我们引入了平均回报来衡量一个策略的好坏，其定义如下：
$$\begin{array}{rl}J(\mathbf{\theta })\doteq r(\pi )& \doteq \underset{h\to \infty }{\lim }\frac{1}{h}\sum _{t=1}^h\mathbb{E}\left[R_t\mid S_0,A_{0:t-1}\sim \pi \right]\\ & =\underset{t\to \infty }{\lim }\mathbb{E}\left[R_t\mid S_0,A_{0:t-1}\sim \pi \right]\\ & =\sum _s\mu (s)\sum _a\pi (a\mid s)\sum _{s^{\prime },r}p\left(s^{\prime },r\mid s,a\right)r\end{array}$$
同样的，μ是策略Π下MDP问题的稳态分布，定义为$\mu (s)\doteq {\lim }_{t\to \infty }\mathrm{Pr}\left\{S_t=s\mid A_{0:t}\sim \pi \right\}$稳态分布的含义就是：如果按照策略Π来选择动作的话，无论状态之间怎么转移，它们的分布是不会变化的。也就是说：
$$\sum _s\mu (s)\sum _a\pi (a\mid s,\mathbf{\theta })p\left(s^{\prime }\mid s,a\right)=\mu \left(s^{\prime }\right),\text{ for all }{s}^{\prime }\in \mathcal{S}$$
continuing task based on AC method
在continuing task中，资格迹的AC方法的伪代码如下：

对actor和critic分别使用资格迹，w参数表示的是更新值函数时的参数；θ参数表示的是更新策略时的参数。
对于连续任务而言，TD error都需要减去均值，也就是上述的$\overline{R}$.
continuing task 的策略梯度理论
结合平均回报的定义，对应的状态值函数和动作值函数分别叫做微分状态值函数和微分动作值函数，定义是：
$v_{\pi }(s)\doteq {\mathbb{E}}_{\pi }[G_t|S_t=s]$和$q_{\pi }(s,a)\doteq {\mathbb{E}}_{\pi }[G_t|S_t=s,A_t=a]$,其中：
$$G_t\doteq R_{t+1}-r(\pi )+R_{t+2}--r(\pi )+...$$
细节内容参考第十章的内容。

连续任务的策略梯度理论证明如下：
（推导一波，感觉用到了不少之前的知识）

7. 连续动作空间的策略参数化

实际环境中，很多任务的动作空间是连续的，比如机器人的控制，如果有一个位置控制器，那么策略的期望输出可以是位置，速度控制也是一样。在连续动作空间中是无法计算每一个动作的概率的，因为有无限个动作。所以可以考虑获得某个动作空间上动作的概率分布。此时要参数化一个策略，这个策略就表达了动作的分布情况。最常用的是正态分布。
$$p(x)\doteq \frac{1}{\sigma \sqrt{2\pi }}\exp \left(-\frac{(x-\mu {)}^2}{2{\sigma }^2}\right)$$

均值和方差分别用来控制概率密度曲线的形状和位置。

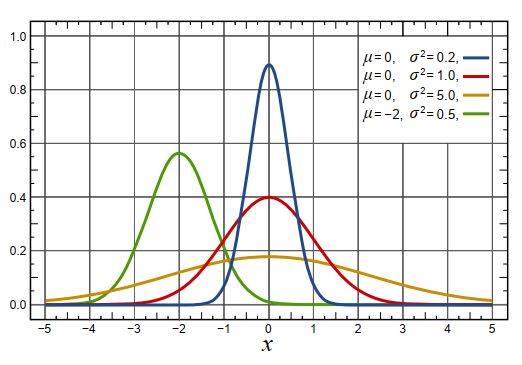
假设某个状态s下策略输出动作a=0的可能性大，那么上图除了绿色曲线之外，其余的曲线均可以刻画期望的动作。如果确定a=0是最优动作，那么我们自然希望动作尽量在a=0附近波动，所以此时蓝色曲线是最合理的。
我们可以通过均值和方差参数化一个策略：

$$\pi (a\mid s,\mathbf{\theta })\doteq \frac{1}{\sigma (s,\mathbf{\theta })\sqrt{2\pi }}\exp \left(-\frac{(a-\mu (s,\mathbf{\theta }){)}^2}{2\sigma (s,\mathbf{\theta }{)}^2}\right).$$
该策略有两个参数$\mathbf{\theta }={\left[{\mathbf{\theta }}_{\mu },{\mathbf{\theta }}_{\sigma }\right]}^{\top }$，分别是均值函数和方差函数的参数。可以用神经网络表示均值函数，也可以是线性函数，如果是线性的：
$$\mu (s,\mathbf{\theta })\doteq {\mathbf{\theta }}_{\mu }^{\top }{\mathbf{x}}_{\mu }(s)$$
${\mathbf{x}}_{\mu }(s)$是基于状态构造的特征向量，对于方差, 它必须是正的，所以可以使用指数形式的参数表达：
$$\sigma (s,\mathbf{\theta })\doteq \exp \left({\mathbf{\theta }}_{\sigma }^{\top }{\mathbf{x}}_{\sigma }(s)\right)$$

也可以用神经网络，但是要注意最后输出层激活函数的选择，必须是一个非负的映射，例如可以选择softplus。通过这种方式参数化策略，实际上就是参数化均值函数和方差函数。

总结

尽管本书仅仅有短短一章的内容讲解策略梯度，这并不代表其不重要，相反，近些年来越来越多的学者比较热衷于研究策略梯度。
策略梯度方法有一些优势，可以学习动作的分布，本质上就具备解决连续动作空间的问题；并且可以更加方便的控制探索的程度，渐进的近似确定性策略；策略梯度具备良好的理论基础，比如策略梯度理论。
本章关于策略梯度方法的讲解，先从episodic task开始，然后再从continuing task入手。介绍了REINFORCE算法，为了较少该算法方差带来的影响，加入baseline缩减方差。接着介绍了AC方法。
策略梯度理论要牢记于心。