简单递归实现二叉树重建

题目（来源 牛客网 剑指Offer 编程题 第四题）：

输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。
假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建二叉树并返回。

正确代码：

/**
 * Definition for binary tree
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
public class Solution {
    public TreeNode reConstructBinaryTree(int [] pre,int [] in) {
        TreeNode treeNode =BinaryTree(pre,0,pre.length-1,in,0,in.length-1);
        return treeNode;
    }

    public static TreeNode BinaryTree(int []pre,int preStart,int preEnd,int []in ,int inStart,int inEnd){
        if (preEnd

解题思路：
题目给出二叉树的前序遍历和中序遍历，要求我们重建二叉树。
根据二叉树前序遍历和中序遍历的特性，我们很快的知道二叉树的根节点就是1。并且在二叉树的中序遍历中很快的分清楚左子树和右子树。

再往下推，在中序遍历里，我们已经分清楚二叉树的左子树部分和右子树部分。根据二叉树的特性：任意一颗二叉树，它的左子树或者右子树存在且深度大于1，那么必定也是一颗二叉树。
在上面这句活中，我们可以画出重点来：
1、分类讨论，左子树和右子树
2、不管左子树或者右子树，那么他们都是二叉树，这里就该用到递归。

接下来的问题就是该怎么递归？
我们可以用中序遍历的左子树和右子树部分，可以确定前序遍历中的左子树和右子树部分。

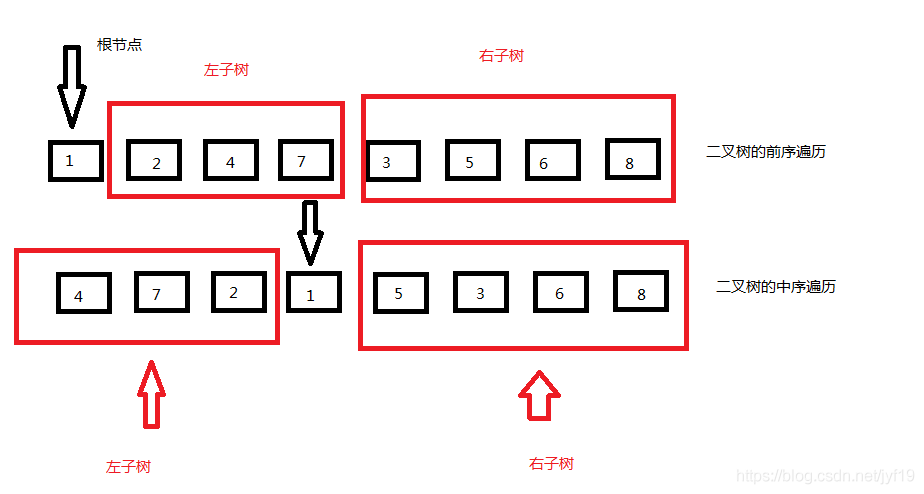
这样就可知，左子树的前序遍历是2,4,7；中序遍历是4,7,2。右子树的前序遍历是3,5,6,8；中序遍历是5,3,6,8。
由此，越来越觉得要用递归了。由大化小，分类讨论，他们的list数组也该这样。所以，前序遍历和中序遍历的数组也应该，分段截取。递归方法的参数，即可确定：前序序列，前序序列的起始下标，前序序列的结束下标，后序序列，后序序列的起始下标，后序序列的结束下标
此时，又引入新的问题：数组应该怎么分段截取，即下标怎么确定？
这是最后的一个问题，也是最重要的一个问题。下面我们捋一遍代码：
首先定义好 递归方法的参数：

BinaryTree(int []pre,int preStart,int preEnd,int []in ,int inStart,int inEnd)

下面对递归做了诠释：

递归的能力在于用有限的语句来定义对象的无限集合。一般来说，递归需要有边界条件、递归前进段和递归返回段。
当边界条件不满足时，递归前进；当边界条件满足时，递归返回。

则边界条件很明显，两个数组的空间随着起始下标和结束下标的变化而变小，当结束下标小于起始下标时：就是到达二叉树叶子节点的时候。即：

if (preEnd

解题思路一开始，我们根据前序和中序的特性，可以确定：

当前二叉树的前序遍历，第一个必为根节点：

 TreeNode treeNode = new TreeNode(pre[preStart]);

根据根节点，我们需要找到，中序遍历中的根节点，以此确定它的左子树和右子树，此时需要一个下标，从中序遍历中找到这个点，而这个点就是前序遍历中的首节点。则会有以下代码：

 for (int i=inStart;i<=inEnd;i++){
            if (pre[preStart]==in[i]){
            	……
            }
            }

此时，我们又找到了递归中的一个临界条件：当确定了根节点，确定它的左子树和右子树部分，即可结束这场相爱相恨的递归。所以可以break了。

但是，我们只是找到它的左子树部分和右子树部分，并没有重构它的左子树和右子树。而且整个代码里，都没有反复的自己调用自己的方法。

诶，此时，就该出现了，我们可以发现TreeNode还有两个参数：left，right还没用到过，并且它们也是TreeNode类型的。所以，再break之前，我们需要把它的left，right重建好。即：

				treeNode.left = BinaryTree(pre,preStart+1,i+preStart-inStart,in,inStart,i-1);
                treeNode.right = BinaryTree(pre,i+1+preStart-inStart,preEnd,in,i+1,inEnd);

则，左子树和右子树都重建好了，则返回结果。

说到最后，我好像还没有说，它们的左子树和右子树下标是怎么确定的：

由上图可知，可得以下条件：
1、我们可以得到根节点的下标：中序遍历（i点）；
2、中序遍历和它的下标（inStart ，inEnd），前序遍历和它的下标（preStart和 preEnd）；
3、中序遍历的左子树和右子树，与 前序遍历的左子树和右子树长度相等

推出以下结论：
1、中序遍历i点左边是左子树，右边是右子树。即可确定参数：左子树（中序遍历(inStart ,i-1) ，长度为i-1-inStart ） 右子树（中序遍历（i+1，inEnd），长度为inEnd-i-1）
2、前序遍历，去除已用的根节点，所剩区间（preStart +1，preEnd）
3、前序遍历区间也可确定：左子树（前序遍历（preStart +1，preStart +1+左子树长度（i-1-inStart ））），右子树（前序遍历（preStart +1+左子树长度（i-1-inStart ）+1，preEnd）） // 即 左子树（前序遍历（preStart +1，preStart +i-inStart ）），右子树（前序遍历（preStart +1+i-inStart，preEnd））

最终确定下标：

				 treeNode.left = BinaryTree(pre,preStart+1,i+preStart-inStart,in,inStart,i-1);
                treeNode.right = BinaryTree(pre,i+1+preStart-inStart,preEnd,in,i+1,inEnd);