利用RSA算法实现文件加密(C++)

了解

    说道加密算法就不得不提起：对称加密算法和非对称加密加密算法

    对称加密算法：甲方选某择一种加密规则，对信息进行加密。乙方使用同一种规则，对信息进行解密。由于加密和解密使用同样规则（简称“密钥”），因此被称为“对称加密算法”

    这种加密模式有一个最大的弱点：甲方必须把加密规则告诉乙方否则无法解密。那么保存和传递密钥就成为了另一个重要问题

   非对称加密算法：可以在不直接传递密钥的 情况下，完成解密。加密和解密 可以使用不同的规则，只要这两种规则之间存在某种对应关系即可，这样就避免了直接传递密钥。这种新的加密模式 被称为"非对称加密算法"。

• 乙方生成两把密钥（公钥和私钥）。公钥是公开的，任何人都可以获得，私钥则是保密的。
• 甲方获取乙方的公钥，然后用它对信息加密。
• 乙方得到加密后的信息，用私钥解密。

  如果公钥加密的信息只有私钥解得开，只要私钥不泄露，就可以保证安全

---

RSA加解密公式

• 加密：公钥（E,N)             密文=(明文^E) mod N
• 解密：密钥（D,N）          明文=(密文^D) mod N

RSA的安全基于大数分解的难度。公钥和私钥是一对大素数的函数。从一个公钥和密文恢复出明文的难度，等价于分解两个大素数之积

主要用到的公式：

1. 互质数：公约数只有1的两个数
2. 欧拉函数：φ（mn）=φ（m）φ（n）=（m-1）x（n-1）
3. 欧拉定理：如果两个正整数a和n互质，则n的欧拉函数φ（n）可以让等式 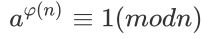 成立
4. 模反元素（逆元）：根据欧拉定理，如果两个正整数a和n互质，那么一定可以找到整数b，使得ab-1可以被n整除或者ab%n=1，b就叫做a的模反元素

---

RSA密钥产生的过程

1. 随机选择两个不相等的质数p和q。
2. 计算p和q的乘积n，n=pq。
3. 计算n的欧拉函数φ（n）。
4. 随机选择一个整数e，条件是1
5. 计算e对于φ（n）的模反元素d，使de=1 mod φ（n）        ——（de）modφ（n）=1
6. 产生公钥（e，n）。私钥（d，n）

举例

1. 选择p=3，q=11.
2. n=pq=33.
3. φ（n）=（p-1）x（q-1）=20.
4. 选择e=3，e与φ（n）互质
5. （de）mod φ（n）=（d*3）mod*20，d=7
6. 公钥（3,33），私钥（7,33）

---

在了解RSA加密算法后，下面开始实际的代码编写
      运行环境windows平台下vs2013

 设计过程：

• 利用rand（）函数产生随机数，并获得两个素数
• 两个素数的乘积产生n，根据欧拉函数求出φ（n）
• 求明文，根据互质的性质，从（1 < e < φ（n））之间随机选取一个数使得e与乘积值互质
• 求密文，根据欧拉定理（（de）mod φ（n） = 1）
• 产生公钥（e，n），私钥（d，n）
• 根据加密公式对字符串、文件内容加密
• 根据解密公式对字符串、文件内容解密

源代码

RSA.h

#pragma once
#include 
#include 
#include 
#include 
#include 

struct Key{
	//公钥(public_key, share_key)
	long long share_key;
	long long public_key;
	//私钥(private_key, share_key)
	long long private_key;
};

class RSA{
public:
	RSA();
	Key GetKey() {
		return _key;
	}
	//给文件进行加密
	void Ecrept(const char* plain_file_in, const char* ecrept_file_out,
		long public_key, long share_key);
	void DEcrept(const char* plain_file_in, const char* ecrept_file_out,
		long private_key, long share_key);

	//对字符串进行加密
	std::vector Ecrept(std::string& str_in, long public_key, long share_key);
	std::string DEcrept(std::vector& ecrept_str, long private_key, long share_key);

	//打印加密之后的信息
	void PrintInfo(std::vector& ecrept_str);
private:
	//产生素数
	long ProducePrime();
	//判断一个数是否是素数
	bool IsPrime(long prime);
	//产生所有的key值
	void ProduceKeys();
	//求share_kay
	long ProduceShareKey(long prime1, long prime2);
	//根据欧拉函数求乘积
	long ProduceOrla(long prime1, long prime2);
	//求public_key
	long ProducePublicKey(long orla);
	//判断两个数之间的最大公约是否为1
	long ProduceGcd(long public_key, long orla);
	//求private_key
	long ProducePrivateKey(long public_key, long orla);
	//加密单个信息
	long Ecrept(long msg, long key, long share_key);
private:
	Key _key;
};

RSA.cpp

#include "RSA.h"

RSA::RSA() {
	ProduceKeys();
}

//给文件进行加密与解密
void RSA::Ecrept(const char* plain_file_in, const char* ecrept_file_out,
	long public_key, long share_key){
	std::ifstream fin(plain_file_in);
	std::ofstream fout(ecrept_file_out, std::ofstream::app);
	if (!fin.is_open()){
		std::cout << "open file failed" << std::endl;
		return;
	}
	//一次读取文件大小，但是有可能因为文件过大，无法进行加密
	//fin.seekg(0, fin.end);
	//long fsize = fin.tellg();
	//按块读取，逐段加密
	const int NUM = 256;
	char buf[NUM];
	long buf_out[NUM];
	int cur_num;
	while (!fin.eof()){
		fin.read(buf, NUM);
		//当前所读取的字节数
		cur_num = fin.gcount();
		for (int i = 0; i < cur_num; ++i){
			buf_out[i] = Ecrept((long)buf[i], public_key, share_key);
		}
		fout.write((char*)buf_out, cur_num * sizeof(long));
	}
	fin.close();
	fout.close();
}
void RSA::DEcrept(const char* plain_file_in, const char* ecrept_file_out,
	long private_key, long share_key){
	std::ifstream fin(plain_file_in);
	std::ofstream fout(ecrept_file_out, std::ofstream::app);
	if (!fin.is_open()){
		std::cout << "open file failed" << std::endl;
		return;
	}
	//一次读取文件大小，但是有可能因为文件过大，无法进行加密
	//fin.seekg(0, fin.end);
	//long fsize = fin.tellg();
	//按块读取，逐段加密
	const int NUM = 256;
	long buf[NUM];
	char buf_out[NUM];
	int cur_num;
	while (!fin.eof()){
		fin.read((char*)buf, NUM * sizeof(long));
		//当前所读取的字节数
		cur_num = fin.gcount();
		cur_num /= sizeof(long);
		for (int i = 0; i < cur_num; ++i){
			buf_out[i] = (char)Ecrept((long)buf[i], private_key, share_key);
		}
		fout.write(buf_out, cur_num);
	}
	fin.close();
	fout.close();
}

//对字符串进行加密与解密
std::vector RSA::Ecrept(std::string& str_in, long public_key, long share_key) {
	std::vector vecout;
	for (const auto& e : str_in){
		vecout.push_back(Ecrept(e, public_key, share_key));
	}
	return vecout;
}
std::string RSA::DEcrept(std::vector& ecrept_str, long private_key, long share_key) {
	std::string strout;
	for (const auto& e : ecrept_str){
		strout.push_back((char)Ecrept(e, private_key, share_key));
	}
	return strout;
}

//打印加密之后的信息
void RSA::PrintInfo(std::vector& ecrept_str) {
	for (const auto& e : ecrept_str){
		std::cout << e << " ";
	}
	std::cout << std::endl;
}

//加密单个信息，模幂运算
long RSA::Ecrept(long msg, long key, long share_key){
	long msg_out = 1;
	long a = msg;
	long b = key;
	int c = share_key;
	while (b){
		if (b & 1){
			//msg_out = (A0*A1...Ai...An) % c
			msg_out = (msg_out * a) % c;
		}
		b >>= 1;
		a = (a * a) % c;
	}
	return msg_out;
}

//产生素数，随机产生两个素数
long RSA::ProducePrime()
{
	srand(time(nullptr));
	long prime = 0;
	while (1){
		prime = rand() % 50 + 2;
		if (IsPrime(prime))
			break;
	}
	return prime;
}

//判断一个数是否是素数
bool RSA::IsPrime(long prime) {
	if (prime < 2)
		return false;
	for (int i = 2; i < sqrt(prime); ++i){
		if (prime % i == 0)
			return false;
	}
	return true;
}

//产生所有的key值
void RSA::ProduceKeys() {
	//选择两个不相等的素数
	long prime1 = ProducePrime();
	long prime2 = ProducePrime();
	while (prime1 == prime2)
		prime2 = ProducePrime();
	_key.share_key = ProduceShareKey(prime1, prime2);
	long orla = ProduceOrla(prime1, prime2);
	_key.public_key = ProducePublicKey(orla);
	_key.private_key = ProducePrivateKey(_key.public_key, orla);
}

//求share_kay
long RSA::ProduceShareKey(long prime1, long prime2) {
	return prime1 * prime2;
}

//根据欧拉函数求乘积
long RSA::ProduceOrla(long prime1, long prime2) {
	return (prime1 - 1) * (prime2 - 1);
}

//求public_key，随机选择一个数， 1 < public_key < orla，public_key,oala互质
long RSA::ProducePublicKey(long orla) {
	long public_key;
	srand(time(nullptr));
	while (1){
		public_key = rand() % orla;
		if (public_key > 1 && ProduceGcd(public_key, orla) == 1)
			break;
	}
	return public_key;
}

//判断两个数之间的最大公约是否为1
long RSA::ProduceGcd(long public_key, long orla) {
	long residual;
	while (residual = public_key % orla){
		public_key = orla;
		orla = residual;
	}
	return orla;
}

//求private_key
long RSA::ProducePrivateKey(long public_key, long orla) {
	//(public_key * private_key) % orla == 1
	long private_key = orla / public_key;
	while (1){
		if ((public_key * private_key) % orla == 1)
			break;
		++private_key;
	}
	return private_key;
}

测试部分

#include "RSA.h"

void TestString() {
	RSA rsa;
	Key key = rsa.GetKey();
	std::string strin;
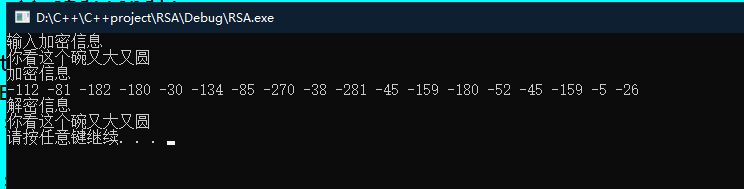
	std::cout << "输入加密信息" << std::endl;
	std::cin >> strin;
	std::vector strecrept = rsa.Ecrept(strin, key.public_key, key.share_key);
	std::string strout = rsa.DEcrept(strecrept, key.private_key, key.share_key);
	std::cout << "加密信息" << std::endl;
	rsa.PrintInfo(strecrept);
	std::cout << "解密信息" << std::endl;
	std::cout << strout << std::endl;
}

//void TestFile() {
//	RSA rsa;
//	Key key = rsa.GetKey();
//	rsa.Ecrept("plain.txt", "ecrept.out.txt", key.public_key, key.share_key);
//	rsa.DEcrept("ecrept.out.txt", "decrept.out.txt", key.private_key, key.share_key);
//}

int main() {
	TestString();
	//TestFile();
	system("pause");
	return 0;
}

运行结果

 字符串加解密：

     

 文件加解密：

 

 

---