医院选址问题--数据结构课程设计

2019年12月份的课程设计。

问题描述：

n个村庄之间的路径用有向加权图表示，要从这n个村庄中选择一个村庄建立一所医院，问这所医院应建在哪个村庄，能使所有的村庄都离这家医院最近（能使离医院最远的村庄到医院最近）或能使所有的村庄到达医院的距离之和达到最小。

我的思路是：

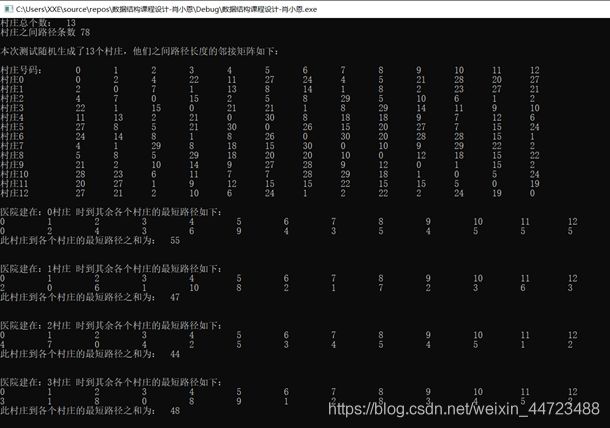
A. 首先是，随机生成了村庄的数量，定义结构变量，通过调用GreateUDN函数给顶点表赋值，随机生成村庄之间的路径长度并存放在邻接矩阵中，即二维数组arcs中，创建完成后调用show函数把村庄间的路径长度的邻接矩阵展示输出，横纵方向显示村庄号码，方便用户直观看出村庄间的路径长度。

B. 因为问题是医院如何选址，因此我先假设医院建在各个村庄，每一次假设，军调用ShortsetPath_DIJ（狄杰特斯拉算法）函数，求出被假设村庄到各个村庄的最短路径，并用一维数组sum记录其到各个村庄的最短路径之和，方便后续比较选择最小者，以最小的那个元素的下标为村庄号码的村庄便是修建医院的最佳地址，可符合题目要求。

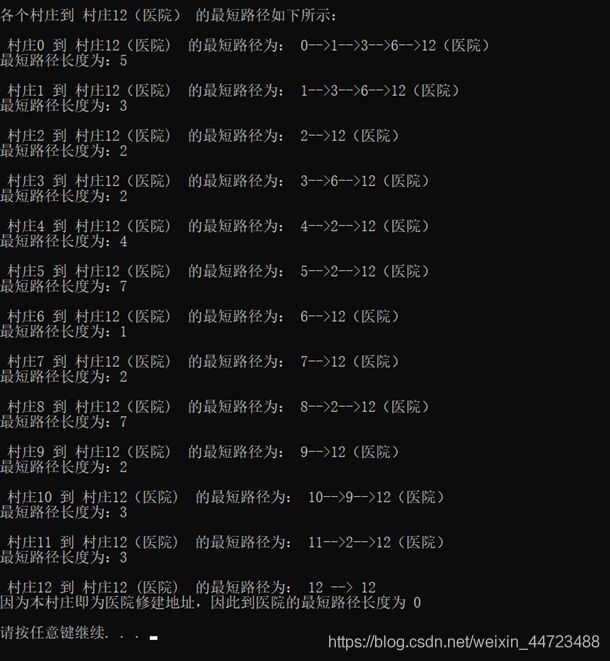
C. 选择好修建医院的村庄后，便需要展示各个村庄到医院的最短路径所经过的村庄路程以及各个村庄到医院的最短路径。此时调用shoeshort函数输出展示路径过程，调用ShortsetPath_DIJ3函数输出各个村庄到医院的最短路径长度（此处仅输出单个村庄到医院的最短路径），循环调用输出过程以及最短路径长度。

D. 期间，编程时注意代码输出格式规整、直观问题。具体结果展示详见结果截图，

以下是完整代码，注释比较详细了，若有问题，欢迎指正！

#include   //用到间隔输出：setw(int）
#include "time.h"    //用到时间函数
#include "math.h"    // 用到随机函数
#include
using namespace std;
#define MaxInt 32767          //表示极大值，即无穷∞
#define MVNum  30         //最大顶点数
typedef int Status;         //1成功  0失败
typedef int VerTexType;      //顶点的数据类型为 int型  即，此处以 0，1，2，3，4...表示村庄
typedef int ArcType;         //边的权值类型为整型  路径长度为整型
typedef  struct
{
     
 VerTexType vexs[MVNum];      //顶点表  存放顶点信息 
 ArcType arcs[MVNum][MVNum];  //邻接矩阵  存放权值，即路径长度
 int vexnum;                  //图当前顶点数  在mian函数中随机生成顶点数，传值到GreateUDN函数构造有向网
 int arcnum;                  //图当前边数    构建完全有向图，根据随机生成的顶点数计算边数
}AMGragh;
bool S[MVNum];              //记录从源点v0到终点vi是否已被确定最短路径长度，1表示确定，0表示尚未确定
int  Path[MVNum][MVNum];    // 记录从源点v0到终点vi的当前最短路径上vi的直接前驱顶点序号。 
int  D[MVNum];             //记录从源点v0到终点vi的当前最短路径长度
int sum[30];               //每个元素都记录着一个村庄到其余各个村庄之间的最短路径之和  
Status GreateUDN(AMGragh &G,int m)  //采用邻接矩阵表示法创建有向网G
{
     
 G.vexnum = m;       //m为main函数中随机生成的一个整型数据  当作顶点数
 cout << "村庄总个数：  " << G.vexnum << endl;
 G.arcnum = m * (m - 1) / 2;    //此处假设村庄以及其路径构成的图为：有向完全图
 cout << "村庄之间路径条数 " << G.arcnum << endl;
 for (int i = 0; i < G.vexnum; ++i)
 {
     
//vexs[MVNum]为顶点表，顶点数据类型是整型，村庄用整形数据表示，共有m个，vex[0]-vexs[m-1]存入村庄0 -（m-1）
 G.vexs[i]=i;
    for (int i = 0; i < G.vexnum; ++i)//初始化 邻接矩阵，边（路径）的权值，均值为最大值MaxInt
 {
     
  for (int j = 0; j < G.vexnum; ++j)
  {
     
   if (i == j)
    G.arcs[i][j] = 0;    //本村庄到本村庄的路径长度为0
   else
    G.arcs[i][j] = MaxInt;   //某村庄到其余各个村庄的路径初始化为MaxInt
  }
 }
 for (int d = 0; d < G.vexnum; d++)
 {
     
  for (int s = 0; s < G.vexnum; s++)
   for(int f=0;f<s;f++)        //考虑到对称，保证对称元素仅操作其中一个  另一个与被操作的 路径长度相等即可
  {
     
   int w = 1 + rand() % 30;//随机生成路径长度，路径长度在1-30之间
   G.arcs[s][f] = G.arcs[f][s] = w;//对称边路径长度相等，即权值相等
  }
 }
 return 1;
}
void show(AMGragh &G)//输出随机生成的结果，即各个村庄之间的路径长度的邻接矩阵
{
     
 cout << "村庄号码："<<'\t';
 for (int i = 0; i < G.vexnum; i++)
 {
     
  cout <<G.vexs[i]<<'\t';
 }
 cout << endl;
 for (int k = 0; k < G.vexnum; k++)
 {
     
   //此处主要是调整好格式，使矩阵输出规整，村庄与村庄之间的路径长度关系直观。
  cout << "村庄" << G.vexs[k]<<'\t'<<'\t';       
  cout << right;
  for (int j = 0; j < G.vexnum; j++)
  {
     
   cout << G.arcs[k][j] <<'\t';//输出随机生成的村庄间路径长度的邻接矩阵
  }
  cout << endl;
 }
}
void ShortsetPath_DIJ(AMGragh G, int v0)//用Dijkstra算法求无向网G的 某个村庄 到 各个村庄 的最短路径
{
     
 int d = 0;    //在后面用以记录某一村庄到各个村庄的最短路径之和，以方便输出 和 保存在数组sum中
 int n = G.vexnum;  //n为G中村庄个数
 int v;
 cout << left;//格式调整
 for (int u = 0; u < G.vexnum; u++)
 {
     
  cout << setw(10) << u;                  //此处输出各个村庄号，与后面的最短路径输出 一一对齐
 }
 cout << endl;
 for (v = 0; v < n; ++v)//n个村庄依次初始化
 {
     
  S[v] = 0;//S初始为空集
  D[v] = G.arcs[v0][v];//将v0到各个终点的最短路径长度初始化为狐上的权值
  if (D[v] < MaxInt)
   Path[v0][v] = v0;//如果v0和v之间有狐，则将v的前驱置为v0
  else
   Path[v0][v] = -1;//否则置为-1
 }
 S[v0] = 1;//将v0加入S
 D[v0] = 0;//源点到源点的距离为0
 //初始化结束，开始主循环     每次求得v0到某个顶点的v的最短路径，将v加到S集
 for (int i = 0; i < n; ++i)//对其余n-1个顶点，依次进行计算
 {
     
  int min = MaxInt;
  for (int w = 0; w < n; ++w)
   if (!S[w] && D[w] < min)
   {
     
    v = w;
    min = D[w];//选择一条当前的最短路径，终点为v
   }
  S[v] = 1;//将v加入S
  for (int w = 0; w < n; ++w)//更新从v0出发到集合V-S上所有村庄的最短路径长度
   if (!S[w] && (D[v] + G.arcs[v][w] < D[w]))
   {
     
    D[w] = D[v] + G.arcs[v][w];//更新D[w]
    Path[v0][w] = v;//更改w的前驱为v
   }
  cout << left; //格式调整
  cout << setw(10) << D[i];  //输出源点到某个点的最短路径长度，与上面的村庄序号一一对应
 }
 for (int x = 0; x < n; x++)
 {
     
  d += D[x];  //求某个顶点到各个顶点之间的最短路径长度之和 用d记录
 }
 //求完一组后，输出这个村庄到各个村庄的最短路径长度之和
 cout << endl<<"此村庄到各个村庄的最短路径之和为：  " << d << endl<<endl;  
 sum[v0] = d;//记录某村庄到各个村庄的最短路径之和，用于后续 选址  选择那个和最小的的
}
void showshort(AMGragh G, int s, int t)//最短路径输出
{
     
 cout << t;
 while (Path[s][t]!= s)
 {
     
  cout << "-->" << Path[s][t];
  t= Path[s][t];
 }
 cout << "-->" << s<<"（医院）"<<endl;   //选择好医院修建地址后，输出各个村庄到医院的最短路径 路径经过过程
}
void ShortsetPath_DIJ3(AMGragh G, int y, int v0)//这个函数  仅输出一个需要的最短路径长度
{
     
 int n = G.vexnum;  //n为G中村庄个数
 int v;
 for (v = 0; v < n; ++v)//n个村庄依次初始化
 {
     
  S[v] = 0;//S初始为空集
  D[v] = G.arcs[v0][v];//将v0到各个终点的最短路径长度初始化为狐上的权值
  if (D[v] < MaxInt)
   Path[v0][v] = v0;//如果v0和v之间有狐，则将v的前驱置为v0
  else
   Path[v0][v] = -1;//否则置为-1
 }
 S[v0] = 1;//将v0加入S
 D[v0] = 0;//源点到源点的距离为0
 //初始化结束，开始主循环     每次求得v0到某个顶点的v的最短路径，将v加到S集
 for (int i = 0; i < n; ++i)//对其余n-1个顶点，依次进行计算
 {
     
  int min = MaxInt;
  for (int w = 0; w < n; ++w)
   if (!S[w] && D[w] < min)
   {
     
    v = w;
    min = D[w];//选择一条当前的最短路径，终点为v
   }
  S[v] = 1;//将v加入S
  for (int w = 0; w < n; ++w)//更新从v0出发到集合V-S上所有村庄的最短路径长度
   if (!S[w] && (D[v] + G.arcs[v][w] < D[w]))
   {
     
    D[w] = D[v] + G.arcs[v][w];//更新D[w]
    Path[v0][w] = v;//更改w的前驱为v
   }
  if (i == y)
  {
     
   cout << "最短路径长度为：" << D[i] << endl << endl;  //此处仅输出该村庄到医院的最短路径
   i = n;          //已得到想要结果并已输出， 令i=n,结束主循环
  }
 }
}
int main()
{
     
  time_t t;   // 定义时间变量
 srand((unsigned)time(&t));  //由时间确定随机序列，执行一次
 int i;
 int m = 1+rand() % 20; //1-20之间  随机生成一个int型数据，当作顶点数
 AMGragh G;  
 GreateUDN(G, m); //构建村庄以及之间路径长度的有向网
 cout <<endl<< "本次测试随机生成了" << m << "个村庄，他们之间路径长度的邻接矩阵如下：" << endl << endl;
 show(G);  //输出展示
 for (int h = 0; h < m; h++)
 {
     
 //循环调用狄杰特斯拉算法，求各个村庄到各个村庄的最短路径
     cout << endl<<"医院建在：" << h <<"村庄 时到其余各个村庄的最短路径如下："<< endl;    
 ShortsetPath_DIJ(G, h);
 }
 cout << "操作 完成啦！";  //狄杰特斯拉算法求最短路径  操作完成！
 int r=0,y =0;
 for ( i = 1; i < m; i++)
 //比较数组sum中的记录着各个村庄到各个村庄的最短路径之和的元素，最小的那个元素的下标即为医院修建地址所在的村庄，
 //这样，可以使得其余各个村庄到医院的路径都最短
 {
     
  if (sum[i] < sum[y])
   y = i;
  else if (sum[i] == sum[y])
   r = i;
 }
 if (r != y||(r==0&&y==0))
  //若是相等且不同时为0，则说明有两个不同村庄到各个村庄的路径之和想等且为最小，
  //此时医院建在两个村庄中任意一个  均可符合题意要求
  cout << endl << endl << "应该选择“村庄" << y << "”来修建医院，此时其余各个村庄到医院的路径都最近！" << endl;
 else
  cout << endl << endl << "应该选择“村庄" << y<<"”或者村庄“" <<r
  <<"”来修建医院，此时其余各个村庄到医院的路径都最近！" << endl;
 //选址完成后，即确定了医院修建在哪个村庄后，求出各个村庄到医院的最短路径走过的村庄序号序列
 cout << endl<<endl<<"各个村庄到 村庄"<<y<<"（医院） 的最短路径如下所示：" << endl<<endl;
 for (int pp = 0; pp < m; pp++)
 {
     
  if(pp==y)
  {
     
   cout << " 村庄" << pp << " 到 村庄"<<y<<" (医院)  的最短路径为： "<<pp<<" --> "<<pp<< endl;
   cout << "因为本村庄即为医院修建地址，因此到医院的最短路径长度为 0 " << endl<<endl;
  }
  else
  {
     
   cout << " 村庄" << pp << " 到 村庄" << y << "（医院)  的最短路径为： ";
   showshort(G,y,pp);        //展示最短路径过程
   ShortsetPath_DIJ3(G, y,pp);//调用函数 仅输出此时的一个村庄到医院的最短路径长度
  }
 }
 system("pause");    //至此程序执行完成
}

运行结果截图：


个人小结：

   我主要是多次运用了狄杰特斯拉算法，每次求解一个村庄到各个村庄的最短路径，
   并用数组sum记录最短路径之和，最终把医院建在以数组sum最小元素的下标为村庄好么的村庄，
   这样子便满足了各个村庄到医院的路径都最短。

如有错漏，欢迎指正！谢谢。
有帮助？那就–>进入传送门吧 希望分享的东西对大家有所帮助！