学习理论-模型选择-2-训练样本数量与误差上界

在模型选择-1-问题引入中我们知道，我们要获得尽可能小的泛化误差。下面让我们一起看看泛化误差与样本数量和模型数量的关系。

当 H 中模型数有限时

证明一致收敛性

我们假设 H={h1,...,hk} ,这里只考虑二分类情况，即 H 中每个模型都能够将样本 X 映射到 {0,1} 。
假如选定 H 中的某个模型 hi ，定义 Z 是一个伯努利随机变量( Z∈{0,1} )，对于样本集 (x,y)∼D ,我们使 Z=I{hi(x)≠y} ，即对于任意样本输入样本，我们用 Z 表示 hi 是否将它误分类。进而我们用 Zj=I{hi(x(j))≠y(j)} 表示第j个样本是否被 hi 误分类。因为我们的样本集满足独立同分布，因此 Zj 也服独立同分布。
回想之前对训练误差的定义: ϵ^(h)=1m∑mi=1I{h(x(i))≠y(i)} ，因此这里我们可以改写成 ϵ^(hi)=1m∑mj=1Zj ，这里的 Zj 是满足伯努利分布的，因此可以利用模型选择-1-问题引入中给出的第二个fact（Hoeffding不等式）得到：

上式说明，对于确定的 hi 当样本数量 m 很大时,训练误差将会非常接近泛化误差（实际误差）。下面将它推广到整个模型集 H ：
首先，令 Ai 代表 |ϵ(hi)−ϵ^(hi)|>γ .我们可得：

第一行是指：我们的模型中只要有一个满足条件即可，或者说至少要有一个满足条件，因为我们只需要选择出一个最好的模型。第二行以及后面的显然是成立的。
两边同时用1减得：

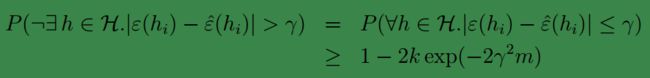
该条件称为，一致性收敛（uniform convergence），它是说明，当m足够大时，假设集中的所有 hi 的训练误差与泛化误差都会很接近。
如果给定 γ 和 δ=2ke−2γ2m 需要多少训练样本才能保证训练误差与泛化误差的差值在 γ 以内的概率为 1−δ 呢？
我们可以得到 m≥12γ2log2kδ .

同样的我们可以固定 m 和 δ 进而求 γ ，得到： |ϵ^(h)−ϵ(h)|≤12mlog2kδ−−−−−−−−√

使用一致收敛性得出结论

基于一致收敛性，
令 h^=argminh∈Hϵ^(h)
令 h∗=argminh∈Hϵ(h)
h^ 是我们的算法选择的模型， h∗ 是模型集中实际上最好的一个。
我们可以得到下面的结论：

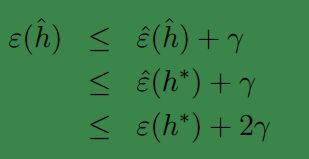
第一行使用了条件 |ϵ(h^)−ϵ^(h^)|≤γ ,第二行的依据是，我们的算法选择 h^ 时，对应的 ϵ^(h) 是最小的。因此对于任意的 ϵ^(h^)≤ϵ^(h) ,故可得第二行；第三行再次使用了一致性收敛条件。
因此，可知，如果满足了一致性收敛，那么我们的算法选择出的模型 h^ 的泛化误差最多比模型集 H 中最好的模型高出 2γ .

因此令 |H|=k ,固定 m,δ 不变，我们有 1−δ 概率可得：

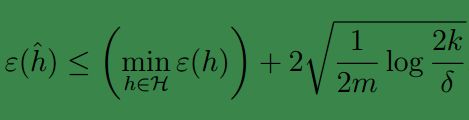
显然不等式右面第二项就是 γ .
这个式子实际上描述了偏差与方差的权衡；当模型数量增加时右面第一项只会减小，不会增大，但是第二项却因为k变大而增大；第一项其实反映了偏差，第二项反映了方差。
令 |H|=k , δ,γ 不变，为了使得 ϵ(h^)≤minh∈Hϵ(h)+2γ 的概率最好少为 1−δ ，可得：

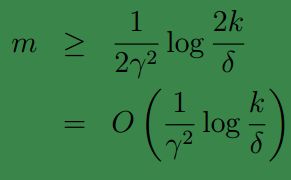
当 H 中模型数无限时

为了简化处理，我们由一个不太严谨的假设开始：
假设 H 中的模型全是线性回归模型，模型的参数有d个，假设一个浮点型在计算机中用64位表示，那么，，那么 H 中可能的假设模型共有 264d 种组合，即 k=264d .这样利用之前证明的结论，为了保证 ϵ(h^)≤ϵ(h∗)+2γ 的概率至少为 1−δ ，需要满足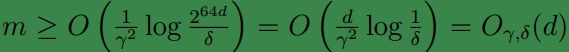
因此，训练样本数量至少与参数数量线性相关。
虽然这个假设不严谨，但是他却是合理的，且可以推广到k为无限大的情况：
因为对于线性回归分类 hθ(x)=I{θ0+θ1x1+...+θnxn≥0} 也可以写成 hu,v(x)=I{(u20−v20)+(u21−v21)x1+...+(u2n−v2n)xn≥0} ，参数数量可以增大到无限，且他们都是模型集 H 中的参数。 H 一直是n维中的线性分类模型的集合。

给定一个新的样本集 X （它和训练样本没有关系）以及类别集合 {y(1),y(2),...,y(d)} ，如果 H 中存在模型 h 使得对于任意的 i=1,...,d 都有 h(x(i))=y(i) ，那么称 H 分散（shatters） S ，即 存在h 能够完美的对 S 中的样本分类。
看下面的图来说明分散问题(shatters)：

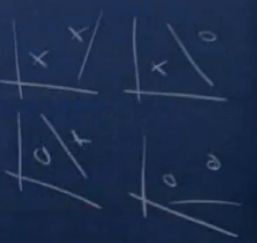
由图可知二维坐标系中的任意两个点必然可以被线性分类器shatter.

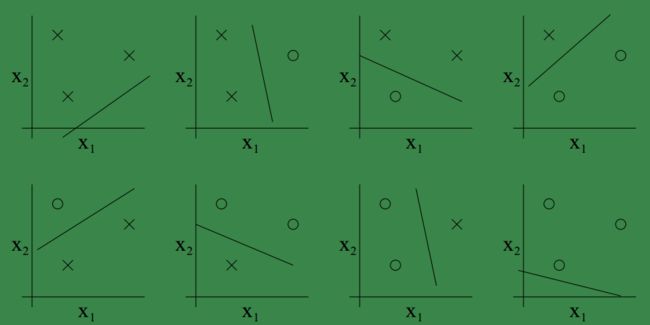
可见二维坐标中的三个点也可以被线性分类器shatter.

显然二维坐标系中的四个点必然存在不能被线性分类器shatter的情况。

给定一个 H ，我们定义它的Vapnik-Chervonenkis dimension（简称VC尺度）为 VC(H) ，VC尺度表示 H 所能shatter的最大的样本数，若 H 能够shatter任意多的样本，那么 VC(H)=∞ .

begin-补充-VC维

在二维坐标系中，三个样本点的情况下存在下面分布情况，左图是三个样本的分布位置，右图是在在这三个位置上可能出现的一种分布情况，显然在这种分布下他是无法被线性分类器shatter的。

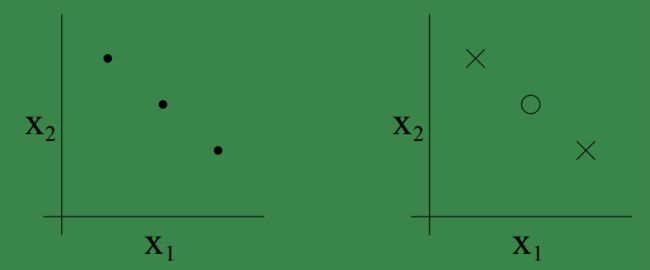
但是，当我们给予这三个点不同的坐标，可以找到使得他们能够被shatter的情况，比如三个点的位置如下，显然这就是我们上面的例子中的分布，基于这三个点的当前位置的所有组合（共 23 个可能组合）都是可以被线性分类器成功分类，因此三个样本是可以被shatter的：

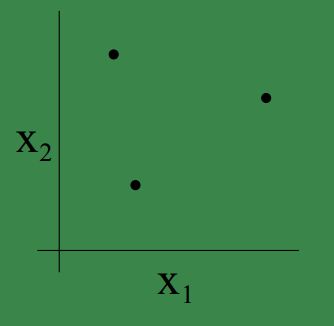
但是对于二维坐标系中的四个点，必然是不能被线性分类器shatter的，即无法给四个样本找到固定的坐标，使得基于当前坐标的 24 种可能的分布都能够被线性分类器成功分类。

因此，线性分类器，在二维坐标系中的VC维 d=3 .

end-补充

下面给出Vapnik和Chervonenkis基于VC维证明得到的结论：
对于某一 H ，已知 d=VC(H) ，那么对于所有的 h∈H ，至少有 1−δ 的概率满足下式：

因此可知，至少有 1−δ 的概率满足下式：

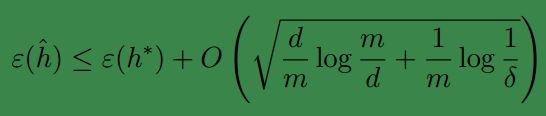
上式说明，当 H 的VC维有限时，那么它随着样本数量m的增加是一致收敛的。

下面得到我们的结论：
对于 h∈H ,为了使得 |ϵ(h)−ϵ^(h)|≤γ （即 ϵ^(h)≤ϵ(h∗)+2γ ）的概率至少为 1−δ ，那么必须有 m=Oγ,δ(d)

因此，训练样本的数量，应该与 H 的VC维呈线性关系。
事实上，实际应用中，VC维基本都是是和训练模型的参数数目相差无几的，因此样本数量也是与样模型参数呈线性关系的。