EM算法-数学原理及其证明

参考http://blog.csdn.net/zouxy09/article/details/8537620
参考 http://www.cnblogs.com/jerrylead

之前介绍了EM算法在混合高斯模型中的应用，现在让我们来看看问什么EM算法可以用于这类问题。
首先介绍一下Jensen 不等式

Jensen 不等式

我们知道，如果设 f 是定义域为实数的函数，如果对于所有的实数 x ， f′′(x)≥0 ，那么 f 是凸函数。
显然我们的样本 x ,是有很多属性的，也就是说函数 f 的输入是一个向量。这时 f 是凸函数就等价为为 f 的 hessian 矩阵 H 是半正定的（ H ≥ 0）。

begin-补充-hessian矩阵

对于一个实值多元函数 f(x1,x2,...,xn) ，如果函数 f 的二阶偏导数都存在，则定义 f 的hessian矩阵为:

H(f)i,j(x⃗ )=DiDjf(x⃗ )

其中 D_i表示对第 i 个变量的微分算子， x⃗ =(x1,x2,...,xn) ,上式展开成矩阵形式如下：

可见如果hessian矩阵存在那么它必然是对称的因为求偏导数时的求导顺序并不影响最终结果：

利用hessian进行多元函数极值的判定:

如果实值多元函数 f(x1,x2,...,xn) 二阶连续可导，我们可以利用某个临界点M处的hessian矩阵判断该临界点是否为极值：
如果H(M)是正定矩阵，则临界点M处是一个局部的极小值。
如果H(M)是负定矩阵，则临界点M处是一个局部的极大值。
如果H(M)是不定矩阵，则临界点M处不是极值。

end-补充-hessian矩阵

如果 f′′(x)≥0 ,那么它的hessian矩阵必然是半正定的，因为hessian矩阵中的每个元素都是有 f 的二阶导数。
下面给出jensen不等式定理：
如果 f 是凸函数， X 是随机变量，那么

E[f(X)]≥f(E[X])

特别地，如果 f 是严格凸函数，那么 E[f(X)]=f(EX) (以后都将f(E[X])表示成f(EX))当且仅当 p(x=E[x])=1 ，即当且仅当 X 是常量时。

为了便于理解咱们先看下面：
凸函数的概念：
【定义】如果函数 f(x) 满足对定义域上任意两个数 x1,x2 都有 f(x1+x22)≥f(x1)+f(x2)2 ，那么 f(x) 为凸函数。
注意哦开口向下的是凸,开口向上的是凹。
如果不等式中等号只有 时才成立，我们分别称它们为严格的凹凸函数.
推广下就是：
对于任意的凹函数 f(x) 以及其定义域上 n 个数 x1,x2,...,xn, 那么都有 f(x1)+f(x2)+...+f(xn)n≥f(x1+x2+...+xnn)
对于任意的凸函数 f(x) 以及其定义域上 n 个数 x1,x2,...,xn ,那么都有 f(x1)+f(x2)+...+f(xn)n≤f(x1+x2+...+xnn)
如果上面凹凸是严格的，那么不等式的等号只有 x1=x2=...=xn 才成立.

其实上面的结论就是我们的jensen不等式，相信大家都见过。
可将jensen用图形表示如下：

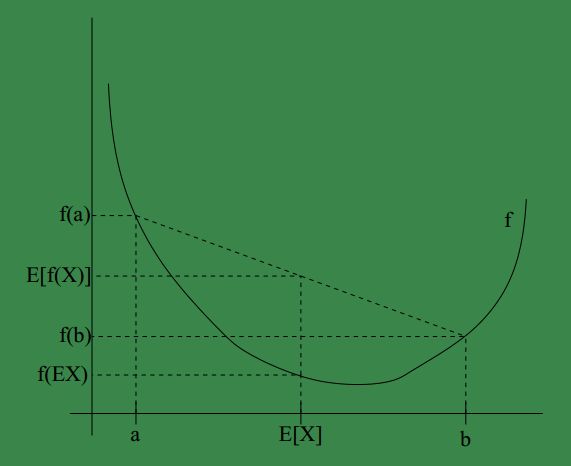
其中 E(X) 就是 a+b2 , E[f(X)] 就是 f(a)+f(b)2 ,显然，在凹函数中 E[f(X)]≥f(E[X]) 。

另外， f 是（严格）凹函数当且仅当 −f 是（严格）凸函数。
Jensen 不等式应用于凸函数时，不等号方向反向，也就是 E[f(X)]≤f(E[X]) .

EM算法

假如我们有训练样本集{ x(1),x(2),...,x(n) },我们之前求模型 p(x,y) 的参数的方式是利用似然值：

但是在上一篇中我们提到由于 z(i) 的值是不确定的随机变量，因此不能通过求最大似然值的方式获得参数。但是一般确定了 z 后，求解就容易了。

EM 是一种解决存在隐含变量优化问题的有效方法。其思想是：不断地建立 ℓ 的下界（ E 步），然后优化下界（ M 步）。这就话没看懂吧！看不懂正常，下面来详细介绍EM算法：
对于每一个样例 i ，让 Qi 表示该样例隐含变量 z 的某种分布， Qi 满足的条件 ∑zQi(z)=1,Qi(z)≥0 (如果 z 是连续性的，那么 Qi 是概率密度函数，需要将求和符号换做积分符号)。
这样我们可以得到：

注：
1、（1）到（2）比较直接，就是分子分母同乘以一个相等的函数。
2、（2）到（3）利用了 Jensen不等式；首先log函数是凸函数。其次根据lazy Statistician规则，可知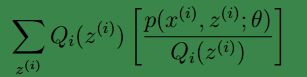其实就是的数学期望，可以看作jensen不等式中的 E[f(X)] ,同理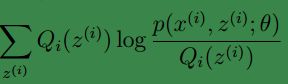可以看作jensen不等式中的 f(E[X]) ；此时根据jensen不等式我们可得：

begin-补充-Lazy Statistician规则

设 Y 是随机变量 X 的函数， Y=g(X) （ g 是连续函数），那么
（1） X 是离散型随机变量，它的分布律为 P(X=xk)=pk，k=1,2,… 。若 ∑∞k=1g(xk)pk 绝对收敛，则有

（2） X 是连续型随机变量，它的概率密度为 f(x) ，若 ∫∞−∞g(x)f(x)dx 绝对收敛，则有

end-补充

因此，对于任何一种分布 Qi ，上面的式子(3)都给 ℓ(θ) 的值确定了一个下限。但是对于 Qi 的选择，有多种可能，那种更好的？
（我们知道，在EM算法中的E步中，我们的 θ 是已知的，即在当前条件下可获得的 θ ）假设 θ 已经给定，那么 ℓ(θ) 的值就决定于 Qi(z(i))和p(x(i),z(i)) 了。我们可以通过调整这两个概率使下界尽可能大（即使得(3)的值尽可能大）， 以逼近 ℓ(θ) 的真实值,显然当(3)等于(2)时 ℓ(θ) 的下限最大。根据jensen不等式我们知道当且仅当 X 是常量时等号成立。这里 p(x(i),z(i);θ)Qi(z(i))就是jensen不等式中的 X ，我们假设 p(x(i),z(i);θ)Qi(z(i))=c⟺p(x(i),z(i);θ)=cQi(z(i))⟺Qi(z(i))=p(x(i),z(i);θ)c
其中 c 是一个不依赖于z^{(i)}的常数。我们知道 ∑zQi(z(i))=1 ，因此可得 ∑zp(x(i),z(i);θ)=∑zcQi(z(i))=c .
进而可得：
Qi(z(i))=p(x(i),z(i);θ)c=p(x(i),z(i);θ)∑zp(x(i),z(i);θ)=p(x(i),z(i);θ)p(x(i);θ)
再利用条件概率公式可得: Qi(z(i))=p(z(i)|x(i);θ)

上面的推导有点乱，现在把他们压缩下就是：

现在我们知道 Qi(z(i)) 该如何选择啦， Qi(z(i)) 的计算公式就是后验概率 p(z(i)|x(i);θ) .
这一步就是 E 步，建立 ℓ(θ) 的下界。接下来的 M 步，就是在给定 Qi(z(i)) 后，调整 θ ，去极大化 ℓ(θ) 的下界（在固定 Qi(z(i)) 后，下界还可以调整的更大）。 一般的 EM 算法的步骤如下：

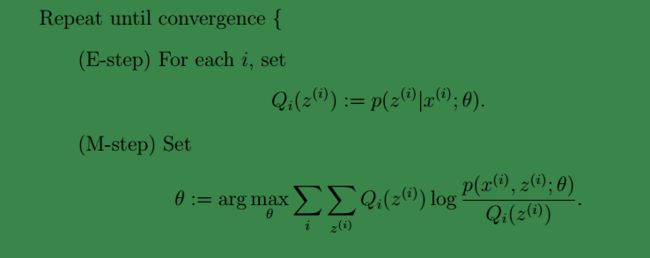
下面让我们来证明EM算法的收敛性：
假定θ(t)和θ(t+1)是 EM 第 t 次和 t+1 次迭代后的结果。 如果我们证明了ℓ(θ(t)) ≤ ℓ(θ(t+1))，也就是说极大似然估计单调增加，那么最终我们会到达最大似然估计的最大值。 下面来证明，选定 θ(t) 后，我们得到 E 步，为了能取等号，选取 Qi(z(i)) 如下：

进而等号满足：

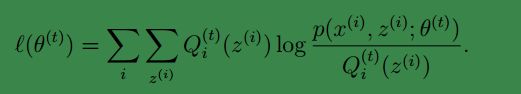
然后我们通过最大化上面等式的式右面获得了新的参数 θt+1 .
此时必然有：

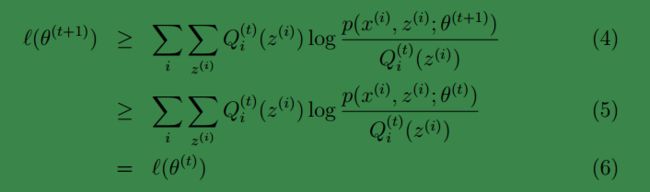
上面第一行是由式（3）得到，即基于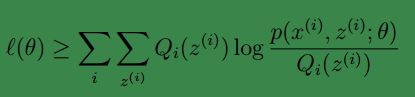
第（ 5）步利用了 M 步的定义。第（ 5）步利用了 M 步的定义， M 步就是将θ(t)调整到θ(t+1)，即 θ(t+1) 的选择是基于：
因此（ 5）成立，（ 6）是之前的等式结果。
这样就证明了ℓ(θ)会单调增加。因此EM算法是收敛的。
如果我们定义：

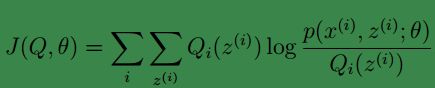
从前面的推导中我们知道ℓ(θ) ≥ J(Q, θ)， EM 可以看作是 J 的坐标上升法， E 步固定θ，优化Q， M 步固定Q优化θ。
下面从别人那偷了张图，很好的说明了EM算法的优化过程：