数据结构与算法(c++)--排序算法
数据结构与算法(c++)–排序算法
这篇文章主要简单记录下数据结构与算法中的排序算法技术
书签
- 插入排序
- 直接插入排序
- 希尔排序
- 交换排序
- 起泡排序
- 快速排序
- 选择排序
- 简单选择排序
- 堆排序
- 归并排序
- 二路归并排序
- 分配排序
- 桶式排序
- 各排序的时空性能
插入排序
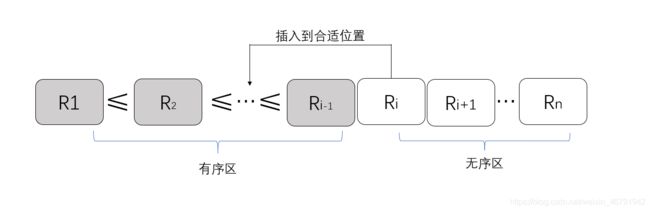
直接插入排序
基本思想:依次将待排序序列中的每一个记录插入到已排好序的序列中,直到全部记录都安排好序。
直接插入排序代码:
void Insertsort(int data[],int length){
//直接插入排序
int i,j,temp;
for (i=1;i<length;i++){
//排序进行length-1次
temp=data[i]; //获取待插元素
for(j=i-1;j>=0&&temp<data[j];j--){
//寻找插入位置
data[j+1]=data[j];
}
data[j+1]=temp;
}
}
希尔排序
基本思想:先将整个待排序记录序列分割成若干个子序列,待整个序列基本有序时,再对全体记录进行一次直接插入排序。
希尔排序代码:
void Shellsort(int data[],int length){
//希尔排序
int d,i,j,temp;
for (d=length/2;d>=1;d=d/2){
//获取增量d,然后再进行这届插入排序
for (i=d;i<length;i++){
temp=data[i]; //获取待插元素
for(j=i-d;j>=0&&temp<data[j];j=j-d)
data[j+d]=data[j];
data[j+d]=temp;
}
}
}
交换排序
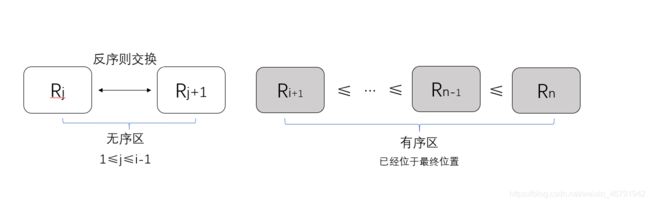
起泡排序
基本思想:两两比较相邻记录,如果反序则交换,直到没有反序的记录为止
起泡排序代码:
void Bubblesort(int data[],int length){
//起泡排序
int j,exchange,bound,temp;
exchange=length-1;//第一趟起泡排序的区间是[0~length-1]
while(exchange!=0){
bound=exchange;
exchange=0;
for(j=0;j<bound;j++){
if(data[j]>data[j+1]){
temp=data[j];
data[j]=data[j+1];
data[j+1]=temp;
exchange=j;
}
}
}
}
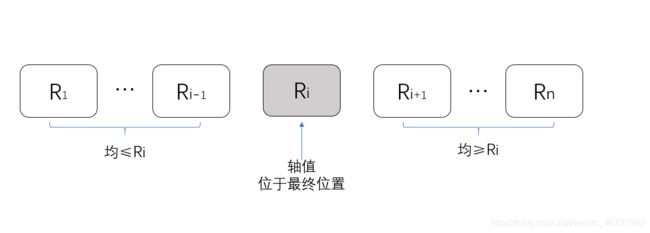
快速排序
基本思想:首先选定一个轴值,将待排序记录划分成两部分,左侧记录均小于或等于轴值,右侧记录均大于或等于轴值,然后分别对这两部分重复上述过程,直到整个序列有序。
快速排序代码:
int Partition(int data[],int first,int last){
//快速排序1
int i=first,j=last,temp;
while(i<j){
while(i<j&&data[i]<=data[j])
j--;
if(i<j){
temp=data[i];
data[i]=data[j];
data[j]=temp;
i++;
}
while(i<j&&data[i]<=data[j])
i++;
if(i<j){
temp=data[i];
data[i]=data[j];
data[j]=temp;
j--;
}
}
return i;
}
void Quicksort(int data[],int first,int last){
//快速排序2
if(first<last){
int pivot = Partition(data,first,last); //一次划分
Quicksort(data,first,pivot-1); //对左侧子序列进行快速排序
Quicksort(data,pivot+1,last); //对右侧子序列进行快速排序
}
}
选择排序
简单选择排序
基本思想:第i趟排序在待排序列中 ri ~ rn(1 ≤ i ≤ n-1)中选取最小的记录,并和第 i 个记录交换作为有序序列的第 i 个记录。
简单选择排序代码
void Selectsort(int data[],int length){
//简单选择排序
int i,j,index,temp;
for(i=0;i<length-1;i++){
index=i;
for(j=i+1;j<length;j++)//在无序区获取最小的序列
if(data[j]<data[index]) index=j;
if(index!=i){
temp=data[i];
data[i]=data[index];
data[index]=temp;
}
}
}
堆排序
基本思想:首先将待排序序列调整成一个堆,此时,选出了堆中所有记录的最大者即堆顶元素,然后将堆顶记录移走,并将剩余记录再调整成堆,这样又找出次大记录,以此类推,直到堆中只有一个记录。
堆排序代码
void Sift(int data[],int k,int last){
//堆排序1
int i=k;
int j=2*i+1;
int temp;
while(j<=last){
if(j<last && data[j]<data[j+1]) j++;
if(data[i]>data[j]) break;
else{
temp=data[i];
data[i]=data[j];
data[j]=temp;
i=j;
j=2*i+1;
}
}
}
void Heapsort(int data[],int length){
//堆排序2
int i,temp;
for(i=ceil(length/2)-1;i>=0;i--){
Sift(data,i,length-1);
}
for(i=1;i<length;i++){
temp=data[0];
data[0]=data[length-i];
data[length-i]=temp;
Sift(data,0,length-i-1); //重建堆
}
}
归并排序
二路归并排序
基本思想:将待排序序列{r1, r2, …,rn}划分为两个长度相等的子序列{r1, r2, …,rn/2}和{rn/2+1, rn/2+2, …,rn},分别对这两个子序列进行排序,得到两个有序子序列,再将这两个有效子序列合并成一个有效子序列。
二路归并排序代码
void Merge(int data[],int first1,int last1,int last2,int length){
//二路归并排序1
int *temp=new int [length+1];//申请辅助空间
int i=first1;
int j=last1+1;
int k=first1;
while(i<=last1&&j<=last2){
if(data[i]<=data[j]) temp[k++]=data[i++];
else temp[k++]=data[j++];
}
while(i<=last1) temp[k++]=data[i++];
while(j<=last2) temp[k++]=data[j++];
for(i=first1;i<=last2;i++) data[i]=temp[i];//辅助空间数据传回数组
delete[] temp;
}
void Mergesort(int data[],int first,int last,int length){
//二路归并排序2
if(first==last) return;//子序列中只有一个记录
else{
int mid=(first+last)/2;
Mergesort(data,first,mid,length);//归并排序左半子序列
Mergesort(data,mid+1,last,length);//归并排序右半子序列
Merge(data,first,mid,last,length);//合并已排序的子序列
}
}
分配排序
桶式排序
基本思想:获取待排序序列中的最大值m,设置m+1个桶,将数值为i的记录分配到第i个桶中,其余无数值的桶为空桶,然后再将各个桶中的记录(忽略空桶)依次取出。
桶式排序代码
int Findmax(int data[],int length){
//桶式排序1
int i,max;
max=data[0];
for(i=1;i<length;i++){
if(data[i]>max)
max=data[i];
}
return max; //获取最大值来创建桶数组
}
void Bucketsort(int data[],int length){
//桶式排序2
int i,m;
m=Findmax(data,length);
int *count=new int[m+1]; //创建桶数组
for(i=0;i<=m;i++) //桶数组全部数值赋予0
count[i]=0;
for(i=0;i<length;i++) //待排序列的数值对应的桶数组下标,并其数值赋予1
count[data[i]]++;
for(i=0;i<=m;i++){
//取出
while(count[i]>0){
cout<<i<<" , ";
count[i]--;
}
}
}
各排序的时空性能
END!