卡方分布
卡方分布
1 卡方分布与伽马分布
若随机变量 χ 2 \chi^2 χ2 服从参数为 n n n的卡方分布 — χ 2 ( n ) \chi^2(n) χ2(n),则它的密度函数是:
p ( x ) = ( 1 2 ) n 2 Γ ( n 2 ) x n 2 − 1 e − x 2 ( x ≥ 0 ) p(x)=\frac{({\frac{1}{2})}^{\frac{n}{2}}}{\Gamma(\frac{n}{2})}x^{\frac{n}{2}-1}e^{-\frac{x}{2}}~~(x\geq0) p(x)=Γ(2n)(21)2nx2n−1e−2x (x≥0)
其中: Γ ( n 2 ) = ∫ 0 + ∞ t n 2 − 1 e − t d t . \Gamma(\frac{n}{2})=\int^{+\infty}_0t^{\frac{n}{2}-1}e^{-t}dt. Γ(2n)=∫0+∞t2n−1e−tdt.
可以看出, χ 2 \chi^2 χ2分布的密度函数与 G a m m a Gamma Gamma分布的密度函数很相似:
f ( y ) = { β α Γ ( α ) y α − 1 e − β y , ( y ≥ 0 ) 0 , ( y < 0 ) f(y)=\left\{ \begin{aligned} \frac{\beta^\alpha}{\Gamma(\alpha)}y^{\alpha-1}e^{-\beta{y}},(y\geq0)\\ ~0,~~~~~~~~~~~(y<0) \end{aligned} \right. f(y)=⎩⎪⎨⎪⎧Γ(α)βαyα−1e−βy,(y≥0) 0, (y<0)
其中, Γ ( α ) = ∫ 0 + ∞ t α − 1 e − t d t \Gamma(\alpha)=\int_0^{+\infty}t^{\alpha-1}e^{-t}dt Γ(α)=∫0+∞tα−1e−tdt.
事实上, χ 2 ( n ) \chi^2(n) χ2(n)等价于 G a ( n 2 , 1 2 ) Ga(\frac{n}{2},\frac{1}{2}) Ga(2n,21). 接下来证明这一点。
服从 χ 2 ( n ) \chi^2(n) χ2(n)的随机变量 χ 2 \chi^2 χ2是 n n n个独立随机变量的组合: χ 2 = X 1 2 + X 2 2 + . . . + X n 2 , \chi^2=X_1^2+X_2^2+...+X_n^2,~~ χ2=X12+X22+...+Xn2, 其中 X 1 , X 2 , . . . , X n X_1,X_2,...,X_n X1,X2,...,Xn独立同分布于标准正态分布N(0,1).
X 1 X_1 X1的密度函数为: p ( x ) = 1 2 π e − x 2 2 p(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}} p(x)=2π1e−2x2 由此可推出 Z = X 1 2 Z=X_1^2 Z=X12的密度函数为:
f ( z ) = { 1 2 π z e − z 2 , ( z ≥ 0 ) 0 , ( z < 0 ) f(z)= \left\{ \begin{aligned} \frac{1}{\sqrt{2\pi}\sqrt{z}}e^{-\frac{z}{2}},(z\geq0)\\ 0,~~~~~~~~~~(z<0)\\ \end{aligned} \right. f(z)=⎩⎪⎨⎪⎧2πz1e−2z,(z≥0)0, (z<0)
证明如下:
F Z ( z ) = P ( Z ≤ z ) = P ( X 1 2 ≤ z ) = P ( − z ≤ X 1 ≤ z ) = F X 1 ( z ) − F X 1 ( − z ) F_Z(z)=P(Z\leq z)=P(X_1^2\leq z)=P(-\sqrt{z}\leq X_1\leq\sqrt{z})=F_{X_1}(\sqrt{z})-F_{X_1}(-\sqrt{z}) FZ(z)=P(Z≤z)=P(X12≤z)=P(−z≤X1≤z)=FX1(z)−FX1(−z)
两边同时求导:
f Z ( z ) = f X 1 ( z ) − f X 1 ( − z ) 2 z = 1 2 π z e − z 2 . f_Z(z)=\frac{f_{X_1}(\sqrt{z}) - f_{X_1}(-\sqrt{z})}{2\sqrt z}=\frac{1}{\sqrt{2\pi}\sqrt{z}}e^{-\frac{z}{2}}. fZ(z)=2zfX1(z)−fX1(−z)=2πz1e−2z.
由于 Γ ( 1 2 ) = ∫ 0 + ∞ t − 1 2 e t d t = π . \Gamma(\frac{1}{2})=\int^{+\infty}_0t^{-\frac{1}{2}}e^tdt=\sqrt{\pi}. Γ(21)=∫0+∞t−21etdt=π.
[ Γ \Gamma Γ函数又称为第二欧拉积分,这个值可以根据余元公式求出,也可以根据正态分布密度函数积分等于1直接得出,可参考https://wenku.baidu.com/view/7042411e561252d381eb6e25.html]
可以看出来 Y = X 1 2 Y=X_1^2 Y=X12 ~ G a ( 1 2 , 1 2 ) Ga(\frac{1}{2},\frac{1}{2}) Ga(21,21).
证明完毕。
由于 G a m m a Gamma Gamma分布具有可加性,即 X 1 X_1 X1 ~ G a ( α 1 , β ) Ga(\alpha_1,\beta) Ga(α1,β), X 2 X_2 X2 ~ G a ( α 2 , β ) Ga(\alpha_2,\beta) Ga(α2,β), X 1 X_1 X1与 X 2 X_2 X2独立,则 Y = X 1 + X 2 Y=X_1+X_2 Y=X1+X2 ~ G a ( α 1 + α 2 , β ) Ga(\alpha_1+\alpha_2, \beta) Ga(α1+α2,β),这个性质可以用卷积公式证明,证明如下:
卷积公式:有相互独立的随机变量 X , Y X,Y X,Y, Z = X + Y Z=X+Y Z=X+Y, 则 f Z ( z ) = ∫ − ∞ + ∞ f X ( x ) f Y ( z − x ) d x f_Z(z)=\int_{-\infty}^{+\infty}f_X(x)f_Y(z-x)dx fZ(z)=∫−∞+∞fX(x)fY(z−x)dx
f Y ( y ) = ∫ − ∞ + ∞ f X 1 ( x ) f X 2 ( y − x ) d x f_Y(y)=\int_{-\infty}^{+\infty}f_{X_1}(x)f_{X_2}(y-x)dx fY(y)=∫−∞+∞fX1(x)fX2(y−x)dx
= ∫ 0 y β α 1 Γ ( α 1 ) x α 1 − 1 e − β x β α 2 Γ ( α 2 ) ( y − x ) α 2 − 1 e − β ( y − x ) d x ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~=\int_{0}^{y}\frac{\beta^{\alpha_1}}{\Gamma(\alpha_1)}x^{\alpha_1-1}e^{-\beta{x}}\frac{\beta^{\alpha_2}}{\Gamma(\alpha_2)}(y-x)^{\alpha_2-1}e^{-\beta{(y-x)}}dx =∫0yΓ(α1)βα1xα1−1e−βxΓ(α2)βα2(y−x)α2−1e−β(y−x)dx
= ∫ 0 y β α 1 + α 2 Γ ( α 1 ) Γ ( α 2 ) x α 1 − 1 ( y − x ) α 2 − 1 e − β y d x ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~=\int_{0}^{y}\frac{\beta^{\alpha_1+\alpha_2}}{\Gamma(\alpha_1)\Gamma(\alpha_2)}x^{\alpha_1-1}(y-x)^{\alpha_2-1}e^{-\beta{y}}dx =∫0yΓ(α1)Γ(α2)βα1+α2xα1−1(y−x)α2−1e−βydx
= β α 1 + α 2 Γ ( α 1 ) Γ ( α 2 ) e − β y ∫ 0 y x α 1 − 1 ( y − x ) α 2 − 1 d x ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~=\frac{\beta^{\alpha_1+\alpha_2}}{\Gamma(\alpha_1)\Gamma(\alpha_2)}e^{-\beta{y}}\int_{0}^{y}x^{\alpha_1-1}(y-x)^{\alpha_2-1}dx =Γ(α1)Γ(α2)βα1+α2e−βy∫0yxα1−1(y−x)α2−1dx
( 令 x y = t ) = β α 1 + α 2 Γ ( α 1 ) Γ ( α 2 ) e − β y y α 1 + α 2 − 1 ∫ 0 1 t α 1 − 1 ( 1 − t ) α 2 − 1 d t ~~~~~~~~~~~~~~~~~~~~~(令\frac{x}{y}=t)~~~~~~~~~~=\frac{\beta^{\alpha_1+\alpha_2}}{\Gamma(\alpha_1)\Gamma(\alpha_2)}e^{-\beta{y}}y^{{\alpha_1+\alpha_2-1}}\int_{0}^{1}t^{\alpha_1-1}(1-t)^{\alpha_2-1}dt (令yx=t) =Γ(α1)Γ(α2)βα1+α2e−βyyα1+α2−1∫01tα1−1(1−t)α2−1dt
= β α 1 + α 2 Γ ( α 1 ) Γ ( α 2 ) e − β y y α 1 + α 2 − 1 B ( α 1 , α 2 ) ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~=\frac{\beta^{\alpha_1+\alpha_2}}{\Gamma(\alpha_1)\Gamma(\alpha_2)}e^{-\beta{y}}y^{{\alpha_1+\alpha_2-1}}B(\alpha_1,\alpha_2) =Γ(α1)Γ(α2)βα1+α2e−βyyα1+α2−1B(α1,α2)
B e t a Beta Beta函数与 Γ \Gamma Γ函数有关系式: B ( a , b ) = Γ ( a ) Γ ( b ) Γ ( a + b ) B(a,b)=\frac{\Gamma(a)\Gamma(b)}{\Gamma(a+b)} B(a,b)=Γ(a+b)Γ(a)Γ(b),这个等式可根据函数的定义通过变量代换证明。
= β α 1 + α 2 Γ ( α 1 + α 2 ) y α 1 + α 2 − 1 e − β y . ~~~~~~~~~~~=\frac{\beta^{\alpha_1+\alpha_2}}{\Gamma(\alpha_1+\alpha_2)}y^{\alpha_1+\alpha_2-1}e^{-\beta{y}}. =Γ(α1+α2)βα1+α2yα1+α2−1e−βy.
证明完毕。
根据 G a m m a Gamma Gamma分布的可加性,很容易得出:
χ 2 ( n ) 等 价 于 G a ( n 2 , 1 2 ) . \chi^2(n)~~等价于~~ Ga(\frac{n}{2},\frac{1}{2}). χ2(n) 等价于 Ga(2n,21).
2 四格表中的卡方拟合优度检验
在检验临床药物有效性的实验设计时,经常会列出一个四格表,然后使用 χ 2 \chi^2 χ2统计量进行拟合优度检验,其原理解释如下。
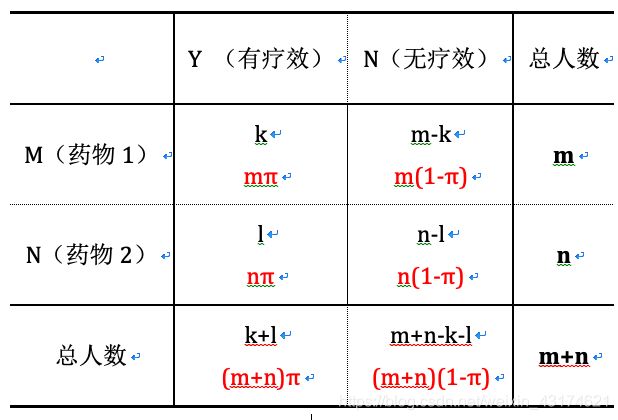
黑色代表的是实际的实验结果,红色代表的是在药物1和药物2药效相同的情况下,理论的实验结果(即在假设药物1与药物2药效相同的情况下的实验结果)。 π \pi π指的是使用两种药物的病人被治愈的概率相等-都为 π \pi π,理论频数等于服用某种药物的人数乘以服用这种药物被治愈的概率。例如,选择 m m m个病人服用药物1,服用药物1被治愈的概率是 π \pi π,那么四格表中 Y − M Y-M Y−M的理论频数就为 m π m\pi mπ.
现在设药物1的有效率为 π 1 \pi_1 π1,现在设药物1的有效率为 π 2 \pi_2 π2.
可以把每一个服用了药物1的病人看作是一个0-1分布,被治愈取1,没有被治愈取0,
则对于药物1来说,相当于做了 m m m次独立的 B e r n o u l l i Bernoulli Bernoulli实验,成功的次数为k. 把成功的次数定为随机变量 K K K, 即 K ∼ B ( m , π 1 ) K\sim B(m,\pi_1) K∼B(m,π1), 根据独立同分布的中心极限定理,有: k − m π 1 m π 1 ( 1 − π 1 ) ∼ ˙ N ( 0 , 1 ) \frac{k-m\pi_1}{\sqrt{m\pi_1(1-\pi_1)}}~\dot{\sim}~N(0,1) mπ1(1−π1)k−mπ1 ∼˙ N(0,1)
随之:
χ 2 = ( k − m π 1 ) 2 m π 1 ( 1 − π 1 ) = ( k − m π 1 ) 2 m π 1 + [ ( m − k ) − m ( 1 − π 1 ) ] 2 m ( 1 − π 1 ) ∼ ˙ χ 2 ( 1 ) \chi^2=\frac{(k-m\pi_1)^2}{m\pi_1(1-\pi_1)}=\frac{(k-m\pi_1)^2}{m\pi_1}+\frac{[(m-k)-m(1-\pi_1)]^2}{m(1-\pi_1)}\dot{\sim}\chi^2(1) χ2=mπ1(1−π1)(k−mπ1)2=mπ1(k−mπ1)2+m(1−π1)[(m−k)−m(1−π1)]2∼˙χ2(1)
同理可得:
χ 2 = ( l − n π 2 ) 2 n π 2 ( 1 − π 2 ) = ( l − n π 2 ) 2 n π 2 + [ ( n − l ) − n ( 1 − π 2 ) ] 2 n ( 1 − π 2 ) ∼ ˙ χ 2 ( 1 ) \chi^2=\frac{(l-n\pi_2)^2}{n\pi_2(1-\pi_2)}=\frac{(l-n\pi_2)^2}{n\pi_2}+\frac{[(n-l)-n(1-\pi_2)]^2}{n(1-\pi_2)}\dot{\sim}\chi^2(1) χ2=nπ2(1−π2)(l−nπ2)2=nπ2(l−nπ2)2+n(1−π2)[(n−l)−n(1−π2)]2∼˙χ2(1)
现在要检验药物1与药物2的药效是否相同,那么原假设与备择假设如下:
H 0 : π 1 = π 2 = π H 1 : π 1 ≠ π 2 H_0:\pi_1=\pi_2=\pi~~~~~~~~~H_1:\pi_1\neq\pi_2 H0:π1=π2=π H1:π1̸=π2
在原假设成立的条件下,有:
( k − m π ) 2 m π ( 1 − π ) + ( l − n π ) 2 n π ( 1 − π ) = ( ( k + l ) − ( m + n ) π ( m + n ) π ( 1 − π ) ) 2 ∼ ˙ χ 2 ( 1 ) \frac{(k-m\pi)^2}{m\pi(1-\pi)}+\frac{(l-n\pi)^2}{n\pi(1-\pi)}=(\frac{(k+l)-(m+n)\pi}{\sqrt{(m+n)\pi(1-\pi)}})^2\dot{\sim}\chi^2(1) mπ(1−π)(k−mπ)2+nπ(1−π)(l−nπ)2=((m+n)π(1−π)(k+l)−(m+n)π)2∼˙χ2(1)
所以可以这样构造 χ 2 \chi^2 χ2 统计量:
( k − m π ) 2 m π + [ ( m − k ) − m ( 1 − π ) ] 2 m ( 1 − π ) + ( l − n π ) 2 n π + [ ( n − l ) − n ( 1 − π ) ] 2 n ( 1 − π ) ∼ ˙ χ 2 ( 1 ) \frac{(k-m\pi)^2}{m\pi}+\frac{[(m-k)-m(1-\pi)]^2}{m(1-\pi)}+\frac{(l-n\pi)^2}{n\pi}+\frac{[(n-l)-n(1-\pi)]^2}{n(1-\pi)}\dot{\sim}\chi^2(1) mπ(k−mπ)2+m(1−π)[(m−k)−m(1−π)]2+nπ(l−nπ)2+n(1−π)[(n−l)−n(1−π)]2∼˙χ2(1)