Task4条件随机场CRF
Task4条件随机场CRF
- 条件随机场概述
-
- 1 产生式模型和判别式模型( Generative model vs Discriminative model )
-
- 1.1 模型简介
- 1.2 模型比较
- 1.3 模型之间的关系
- 2 概率图模型( Graphical Models )
- 3 朴素贝叶斯分类器( Naive Bayes Classifier )
- 4 隐马尔可夫模型( Hidden Markov Model,HMM )
- 5 最大熵马尔可夫模型( MEMM )
- 6 条件随机场( conditional random fields,CRF )
-
- 6.1 CRF定义
- 6.2 CRF线性模型
- 6.3 例子说明
条件随机场概述
条件随机场模型是Lafferty于2001年,在最大熵模型和隐马尔科夫模型的基础上,提出的一种判别式概率无向图学习模型,是一种用于标注和切分有序数据的条件概率模型。
CRF最早是针对序列数据分析提出的,现已成功应用于自然语言处理(Natural Language Processing, NLP)、 生物信息学、机器视觉及网络智能等领域。
与条件随机场相关的各模型之间的关系
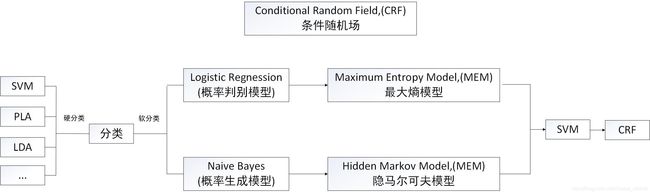
1 产生式模型和判别式模型( Generative model vs Discriminative model )
1.1 模型简介
假设有两个序列,分别为观察序列o和标记序列s
-
产生式模型:构建o和s的联合分布p(s,o),可以根据联合概率来生成样本,如HMM,BNs,MRF。
-
无穷样本->概率密度模型=产生模型->预测
-
判别式模型:构建o和s的条件分布p(s|o),因为没有s的知识,无法生成样本,只能判断分类,如SVM,CRF,MEMM。
-
有限样本->判别函数=预测模型->预测
1.2 模型比较
Generative model :从统计的角度表示数据的分布情况,能够反映同类数据本身的相似度,不关心判别边界。
- 优点:
实际上带的信息要比判别模型丰富,研究单类问题比判别模型灵活性强能更充分的利用先验知识
模型可以通过增量学习得到 - 缺点:
学习过程比较复杂
在目标分类问题中易产生较大的错误率
Discriminative model :寻找不同类别之间的最优分类面,反映的是异类数据之间的差异。
- 优点:
分类边界更灵活,比使用纯概率方法或生产模型得到的更高级。能清晰的分辨出多类或某一类与其他类之间的差异特征。在聚类、viewpoint changes, partial occlusion and scale variations中的效果较好适用于较多类别的识别 - 缺点:
不能反映训练数据本身的特性。
能力有限,可以告诉你的是1还是2 ,但没有办法把整个场景描述出来。
1.3 模型之间的关系
二者关系:由生成模型可以得到判别模型,但由判别模型得不到生成模型。
2 概率图模型( Graphical Models )
概率图模型:是一类用图的形式表示随机变量之间条件依赖关系的概率模型是概率论与图论的结合。图中的节点表示随机变量,缺少边表示条件独立假设。
根据图中边有无方向。常用的概率图模型分为两类:
- 有向图:最基本的是贝叶斯网络(Bayesian Networks ,BNs)
eg:

- 无向图:马尔可夫随机场(Markov Random Fields, MRF)
马尔可夫随机场模型中包含了一组具有马尔可夫性质的随机变量,这些变量之间的关系用无向图来表示。
eg:
有向图模型和无向图模型的对比 - 1共同之处
将复杂的联合分布分解为多个因子的乘积 - 2不同之处
无向图模型因子是势函数,需要全局归一
有向图模型因子是概率分布、无需全局归一 - 3优缺点
无向图模型中势函数设计不受概率分布约束,设计灵活,但全局归代价高有向图模型无需全局归一、训练相对高效
3 朴素贝叶斯分类器( Naive Bayes Classifier )
设x∈Ω是一一个类别未知的数据样本, Y为类别集合,若数据样本x属于一个特定的类别y(j) ,那么分类问题就是决定P(y(j)|x),即在获得数据样本x时,确定x的最佳分类。所谓最佳分类,一种办法是把它定义为在给定数据集中不同类别y先验概率的条件下最可能的分类。贝叶斯理论提供了计算这种可能性的一种直接方法。
前面学过了这里只给出概率图表示:
朴素贝叶斯分类器的概率图表示
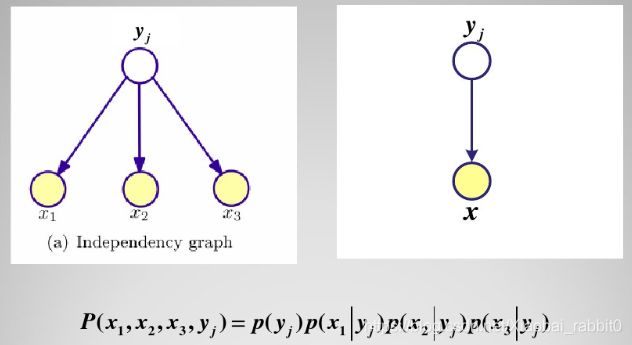
朴素贝叶斯是分类问题,y非0即1,如果y不止0,1两个值,如果是一个标注序列,那么就引申到隐马尔可夫模型了。
4 隐马尔可夫模型( Hidden Markov Model,HMM )
- HMM是一个五元组λ= (Y,X,Π,A,B) ,
其中Y是隐状态(输出变量)的集合,) X是观察值(输入)集合,Π是初始状态的概率, A是状态转移概率矩阵,B是输出观察值概率矩阵。 - 有两个假设:
齐次一阶Markov
观测独立
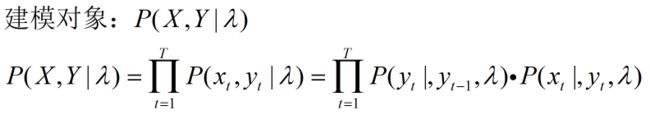
5 最大熵马尔可夫模型( MEMM )
6 条件随机场( conditional random fields,CRF )
简单说就是把MEMM的有向图变为无向图
打破了HMM的齐次Markov问题,这也是MEMM所没解决的问题

-
简单地讲,随机场可以看成是一组随机变量的集合 (这组随机变量对应同一个样本空间)。当给每一个位置按照某种分布随机赋予一个值之后其全体就叫做随机场。
-
当然,这些随机变量之间可能有依赖关系,一般来说,也只有当这些变量之间有依赖关系的时候,我们将其单独拿出来看成一个随机场才有实际意义。
-
**马尔科夫随机场( MRF )**对应一个无向图。这个无向图上的每一 个节点对应一个随机变量,节点之间的边表示节点对应的随机变量之间有概率依赖关系。因此, MRF的结构本质上反应了我们的先验知识- - 一哪些变量之间有依赖关系需要考虑,而哪些可以忽略。
-
具有马尔科夫性质:离当前因素比较遥远(这个遥远要根据具体情况自己定义)的因素对当前因素的性质影响不大。
-
现在,如果给定的MRF中每个随机变量下面还有观察值,我们要确定的是给定观察集合下,这个MRF的分布,也就是条件分布,那么这个MRF就称为CRF。它的条件分布形式完全类似于MRF的分布形式,只不过多了一个
观察集合x。 -
最通用角度来看, CRF本质上是给定了观察值(observations)集合的MRF。
6.1 CRF定义
6.2 CRF线性模型

简化形式
因为条件随机场中同一特征在各个位置都有定义,所以可以对同一个特征在各个位置求和,将局部特征函数转化为一个全局特征函数,这样就可以将条件随机场写成权值向量和特征向量的内积形式,即条件随机场的简化形式。

基本问题
条件随机场包含概率计算问题、学习问题和预测问题三个问题。
- 概率计算问题:已知模型的所有参数,计算观测序列 出现的概率,常用方法:前向和后向算法;
- 学习问题:已知观测序列 ,求解使得该观测序列概率最大的模型参数,包括隐状态序列、隐状态间的转移概率分布和从隐状态到观测状态的概率分布,常用方法:Baum-Wehch 算法;
- 预测问题:一直模型所有参数和观测序列 ,计算最可能的隐状态序列 ,常用算法:维特比算法。
6.3 例子说明
import numpy as np
class CRF(object):
'''实现条件随机场预测问题的维特比算法
'''
def __init__(self, V, VW, E, EW):
'''
:param V:是定义在节点上的特征函数,称为状态特征
:param VW:是V对应的权值
:param E:是定义在边上的特征函数,称为转移特征
:param EW:是E对应的权值
'''
self.V = V #点分布表
self.VW = VW #点权值表
self.E = E #边分布表
self.EW = EW #边权值表
self.D = [] #Delta表,最大非规范化概率的局部状态路径概率
self.P = [] #Psi表,当前状态和最优前导状态的索引表s
self.BP = [] #BestPath,最优路径
return
def Viterbi(self):
'''
条件随机场预测问题的维特比算法,此算法一定要结合CRF参数化形式对应的状态路径图来理解,更容易理解.
'''
self.D = np.full(shape=(np.shape(self.V)), fill_value=.0)
self.P = np.full(shape=(np.shape(self.V)), fill_value=.0)
for i in range(np.shape(self.V)[0]):
#初始化
if 0 == i:
self.D[i] = np.multiply(self.V[i], self.VW[i])
self.P[i] = np.array([0, 0])
print('self.V[%d]='%i, self.V[i], 'self.VW[%d]='%i, self.VW[i], 'self.D[%d]='%i, self.D[i])
print('self.P:', self.P)
pass
#递推求解布局最优状态路径
else:
for y in range(np.shape(self.V)[1]): #delta[i][y=1,2...]
for l in range(np.shape(self.V)[1]): #V[i-1][l=1,2...]
delta = 0.0
delta += self.D[i-1, l] #前导状态的最优状态路径的概率
delta += self.E[i-1][l,y]*self.EW[i-1][l,y] #前导状态到当前状体的转移概率
delta += self.V[i,y]*self.VW[i,y] #当前状态的概率
print('(x%d,y=%d)-->(x%d,y=%d):%.2f + %.2f + %.2f='%(i-1, l, i, y, \
self.D[i-1, l], \
self.E[i-1][l,y]*self.EW[i-1][l,y], \
self.V[i,y]*self.VW[i,y]), delta)
if 0 == l or delta > self.D[i, y]:
self.D[i, y] = delta
self.P[i, y] = l
print('self.D[x%d,y=%d]=%.2f\n'%(i, y, self.D[i,y]))
print('self.Delta:\n', self.D)
print('self.Psi:\n', self.P)
#返回,得到所有的最优前导状态
N = np.shape(self.V)[0]
self.BP = np.full(shape=(N,), fill_value=0.0)
t_range = -1 * np.array(sorted(-1*np.arange(N)))
for t in t_range:
if N-1 == t:#得到最优状态
self.BP[t] = np.argmax(self.D[-1])
else: #得到最优前导状态
self.BP[t] = self.P[t+1, int(self.BP[t+1])]
#最优状态路径表现在存储的是状态的下标,我们执行存储值+1转换成示例中的状态值
#也可以不用转换,只要你能理解,self.BP中存储的0是状态1就可以~~~~
self.BP += 1
print('最优状态路径为:', self.BP)
return self.BP
def CRF_manual():
S = np.array([[1,1], #X1:S(Y1=1), S(Y1=2)
[1,1], #X2:S(Y2=1), S(Y2=2)
[1,1]]) #X3:S(Y3=1), S(Y3=1)
SW = np.array([[1.0, 0.5], #X1:SW(Y1=1), SW(Y1=2)
[0.8, 0.5], #X2:SW(Y2=1), SW(Y2=2)
[0.8, 0.5]])#X3:SW(Y3=1), SW(Y3=1)
E = np.array([[[1, 1], #Edge:Y1=1--->(Y2=1, Y2=2)
[1, 0]], #Edge:Y1=2--->(Y2=1, Y2=2)
[[0, 1], #Edge:Y2=1--->(Y3=1, Y3=2)
[1, 1]]])#Edge:Y2=2--->(Y3=1, Y3=2)
EW= np.array([[[0.6, 1], #EdgeW:Y1=1--->(Y2=1, Y2=2)
[1, 0.0]], #EdgeW:Y1=2--->(Y2=1, Y2=2)
[[0.0, 1], #EdgeW:Y2=1--->(Y3=1, Y3=2)
[1, 0.2]]])#EdgeW:Y2=2--->(Y3=1, Y3=2)
crf = CRF(S, SW, E, EW)
ret = crf.Viterbi()
print('最优状态路径为:', ret)
return
if __name__=='__main__':
CRF_manual()










