相关分析和回归分析
数值型自变量和数值型因变量之间关系的分析方法--相关与回归分析
相关与回归是处理变量之间关系的一种统计方法。
（1）从所处理的变量多少来看
若研究的是两个变量之前的关系，则称为简单相关与简单回归分析；
若研究的是两个以上变量之间的关系，则称为多元相关与多元回归；
（2）从变量之间的关系形态来看，有
线性相关与线性回归分析；
非线性相关与非线性回归分析；
统计分析的目的在于根据统计数据确定变量之间的关系形态及关联的程度，并探索内在的数量规律。
人们在实践中发现，变量之间的关系可分为两种类型，即函数关系和相关关系。
函数关系是一一对应的确定关系。
函数关系的特点：当一个变量的取值确定时，另一个变量的取值也得到确定。
相关关系是变量之间存在的不确定的数量关系。
相关关系的特点：
一个变量的取值不能由另一个变量唯一确定，当变量x取某个值时，变量y的取值可能有几个。
相关分析就是对两个变量之间线性关系的描述与度量。
相关分析要解决的问题有哪些？
- 变量之间是否存在关系？
- 如果存在关系，它们之间是什么样的关系？
- 变量之间的关系强度如何？
- 样本所反映的变量之间的关系能够代表总体变量之间的关系？
为了解决这些问题，在进行相关分析时， 对总体主要有以下两个假定：
- 两个变量是线性关系。
- 两个变量都是随机变量。
注意：在进行相关分析时，首先需要绘制散点图来判断变量之间的关系形态，如果是线性关系，则可以利用相关关系系数来测度两个变量之间的关系强度，然后对相关系数进行显著性检验，以判断样本所反映的关系能否代表两个变量总体上的关系。
散点图是描述变量之间关系的一种直观方法，从中可以大体上看出变量之间的关系形态及关系强度。
（一）相关关系的表现形态
相关关系的表现形态大体上可分为
- 线性相关【若变量之间的关系近似地表现为一条直线】--正线性相关和负线性相关
- 非线性相关【若变量之间的关系近似地表现为一条曲线】
- 完全相关【若一个变量的取值完全依赖于另一个变量，各观测点落在一条直线上】--正线性相关和负线性相关
- 不相关【若两个变量的观测点很分散，无任何规律】
在线性相关中，
若两个变量的变动方向相同，一个变量的数值增加，另一个变量的数值也随之增加， 或一个变量的数值减少，另一个变量的数值也随之减少，则称为正相关；
若两个变量的变动方向相反，一个变量的数值增加，另一个变量的数值也随之减少， 或一个变量的数值减少，另一个变量的数值也随之增加，则称为负相关；
（二）相关系数
相关系数：是根据样本数据计算的度量两个变量之间线性关系强度的统计量。
（三）相关系数r的显著性检验
检验步骤如下：
第一步：提出假设。
第二步：计算检验的统计量。
第三步：进行决策。
根据给定的显著性水平
和自由度
查t分布表，得出
的临界值。若
，则拒绝原假设
, 表明总体的两个变量之间存在显著性的线性关系。
一元线性回归
相关分析的目的在于测度变量之间的关系强度，它所使用的测度工具就是相关系数。
回归分析侧重于考察变量之间的数量关系，并通过一定数学表达式将这种关系描述出来，进而确定一个或几个自变量的变化对因变量的影响程度。
回归分析主要解决以下几个方面的问题：
- 从一组样本数据出发，确定变量之间的数学关系式
- 对这些关系式的可信程度进行各种统计检验，并从影响某一特定变量的诸多变量中找到哪些变量的影响显著的， 哪些是不显著的。
- 利用所求的关系式，根据一个或几个变量的取值来估计或预测另一个特定变量的取值，并给出这种估计或预测的可靠程度。
一元线性回归模型
在回归分析中，被预测或被解释的变量称为因变量；用来预测或解释因变量的一个或多个变量称为自变量。
- 回归模型：
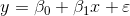
描述因变量
如何依赖于自变量
和误差项
的方程称为回归模型。
式中， 
反映了由于的变化而引起的的线性变化；是被称为误差项的随机变量，它反映了除了和之间的线性关系之外的随机因素对的影响，是不能由和之间的象形关系所解释的变异性。
- 回归方程:
描述因变量的期望值如何依赖于自变量的方程称为回归方程。
式中， 
是回归直线在轴上的截距，是当
时的期望值；
是直线的斜率，表示每变动一个单位时， 的平均变动值。
- 估计的回归方程:
由于总体回归参数和是未知的， 必须利用样本数据估计它们。用样本统计量 
和
代替回归方程中的位置参数和， 这时就得到了估计的回归方程。
式中， 是估计的回归直线在轴上的截距；是直线的斜率，表示每变动一个单位时， 的平均变动值。
最小二乘法（最小平方法）：是通过使因变量的观测值
与估计值
之间的离差平方和达到最小来估计和的方法。
用最小二乘法拟合的直线具有一些优良的性质：
- 根据最小二乘法得到的回归直线能使离差平方和达到最小；
- 由最小二乘法求得的回归直线可知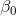和的估计量的抽样分布；
- 在某些条件下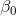，和的最小二乘估计量同其他估计量相比，其抽样分布具有较小的标准差；
根据最小二乘法，使
最小。
令
， 在给定样本数据后，
是和的函数， 且最小值总是存在。
根据微积分的极值定理，对求相应于和的偏导系数，令其等于0，便可求出和， 即
回归直线的拟合优度
回归直线与各观测点的接近程度称为回归直线对数据的拟合优度。
为说明直线的拟合优度，需计算判定系数。
总平方和SST
回归平方和
残差平方和
判定系数
估计标准误差
注意：回归分析的主要目的是根据所建立的估计方程用自变量来估计或预测因变量的取值。建立了估计方程后，还不能马上进行估计或预测，因为该估计方程式根据样本数据得出的， 它是否真实地反映了变量和之间的关系，需要通过检验来证实。
回归分析中的显著性检验主要包括两方面内容：
- 线性关系的检验
- 回归系数的检验
（一）线性关系的检验
线性关系检验：是检验自变量和因变量之间的线性关系是否显著，或者说，它们之间能否用一个线性模型来表示。为检验两个变量之间的线性关系是否显著，需要构造用于检验的统计量。该统计量的构造是以SSR和SSE为基础的。
均方回归
均方残差
F检验统计量：
线性关系检验步骤如下：
第一步：提出假设
两个变量之间的线性关系不显著
第二步：计算检验的统计量。
第三步：作出决策。确定显著性水平，并根据分子自由度
和分母自由度
查F分布表，找到相应的临界值
。若
，拒绝，表明两个变量之间的线性关系是显著的；若
，不拒绝， 没有证据表明两个变量之间的线性关系显著。
（二）回归系数的检验
回归系数的显著性检验是检验自变量对因变量的影响是否显著。
回归系数的显著性检验就是检验回归系数是否等于0。为检验原假设
是否成立，需要构造用于检验的统计量。
的估计的标准差为：
用于检验回归系数的统计量
:
该统计量服从自由度为n-2的t分布。如果原假设成立，则
，检验的统计量为：
回归系数的显著性检验步骤如下：
第一步：提出检验
；
第二步：计算检验统计量。
第三步：作出决策。确定显著性水平，并根据自由度查t分布表，找到相应的临界值
。若，则拒绝，回归系数等于0的可能性小于， 表明自变量对因变量的影响是显著的，换言之，两个变量之间存在着显著的线性关系；若
，则不拒绝， 没有证据表明对的影响显著，或者说，二者之间尚存在显著的线性关系。
回归分析的似然函数
