轻松解剖数据降维——PCA

为什么要进行数据降维？

我们知道数据降维是减少过拟合的重要方法之一，且对于高维度的数据，不仅计算量庞大的吓人，而且容易带来维度灾难。

下面我们从几何角度看看什么是维度灾难，会带来哪些影响？
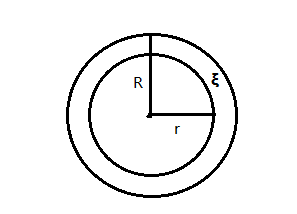
下图是一个同圆心构成的圆环，大圆半径为R = 1，圆环间隙$\xi$足够小，即趋于0，小圆半径为r = R - $\xi$ = 1 - $\xi$。
在二维平面上大圆和小圆的面积几乎相等，圆环的面积趋于0.
$$\frac{V小圆}{V大圆}=\underset{\xi \to 0,k=2}{\lim }\frac{\pi (1-\xi {)}^2}{\pi 1^2}=1\text{\hspace{1em}(1)}$$
如果将下图映射到一个k维空间时，假设k很大，区域 + $\infty$ 。
那么可得：
$$\frac{V小圆}{V大圆}=\underset{\xi \to 0,k\to +\infty }{\lim }\frac{\pi (1-\xi {)}^k}{\pi 1^k}=\frac{0}{1}=0\text{\hspace{1em}(2)}$$
$$\frac{V圆环}{V大圆}=\underset{\xi \to 0,k\to +\infty }{\lim }\frac{\pi 1^2-\pi (1-\xi {)}^k}{\pi 1^k}=\frac{1-0}{1}=1\text{\hspace{1em}(3)}$$

总结：低维数据映射到高维数据，会使得数据变得更加稀疏，分布不均匀，且几乎只有原先边缘部分的数据是分散在高维空间内。这样带来的不好现象就被称为维度灾难。

中心矩阵是什么？

先不急说中心矩阵是什么？有什么作用？有什么性质？我们可以利用均值和协方差矩阵来引出它。
假设有N个样本数据，每个数据是P维特征，用矩阵X来表示这些数据。
向量 x_i 没有说明，默认都是列向量。
$$X_{np}={\left[\begin{array}{c}{x}_1,x_2...,x_n\end{array}\right]}^T=\left[\begin{array}{c}{x}_1^T\\ x_2^T\\ ...\\ x_n^T\end{array}\right]={\left[\begin{array}{cccc}{x}_{11}& x_{12}& ...& x_{1p}\\ x_{21}& x_{22}& ...& x_{2p}\\ ......& & & \\ x_{n1}& x_{n2}& ...& x_{np}\end{array}\right]}_{np}\text{\hspace{1em}(4)}$$

• 样本均值

实际上是求所有样本在不同特征下的均值，故最后结果为 p维的列向量.
设1_n = ${\left[\begin{array}{c}1\\ 1\\ ...\\ 1\end{array}\right]}_{n\times 1}$，矩阵I_n是n维的单位矩阵。

$${\overline{x}}_p=\frac{1}{n}\sum _{i=1}^n{x}_i=\frac{1}{n}{X}^T{1}_n\text{\hspace{1em}(5)}$$

• 样本协方差矩阵

协方差矩阵符号记为S。

$$S_{pp}=\frac{1}{n}\sum _{i=1}^n(x_i-\overline{x})(x_i-\overline{x}{)}^T\text{\hspace{1em}(6)}$$
$$\begin{gathered} S_{pp}=\frac{1}{n}(x_1-\overline{x},x_2-\overline{x},...,x_n-\overline{x})(x_1-\overline{x},x_2-\overline{x},...,x_n-\overline{x}{)}^T \\ =\frac{1}{n}[(x_1,x_2,...,x_n)-\overline{x}(1,1,...,1{)}_n][(x_1,x_2,...,x_n)-\overline{x}(1,1,...,1{)}_n{]}^T \\ =\frac{1}{n}(X^T-\overline{x}{1}_n^T)(X^T-\overline{x}{1}_n^T{)}^T \\ 将式(5)带入可得 \\ {S}_{pp}=\frac{1}{n}(X^T-\frac{1}{n}{X}^T{1}_n{1}_n^T)(X^T-\frac{1}{n}{X}^T{1}_n{1}_n^T{)}^T \\ =\frac{1}{n}[X^T(I_n-\frac{1}{n}{1}_n{1}_n^T)][X^T(I_n-\frac{1}{n}{1}_n{1}_n^T){]}^T \\ =\frac{1}{n}{X}^T(I_n-\frac{1}{n}{1}_n{1}_n^T)(I_n-\frac{1}{n}{1}_n{1}_n^T{)}^{T}X \\ 令H_n=I_n-\frac{1}{n}{1}_n{1}_n^T，则可得 \\ {S}_{pp}=\frac{1}{n}{X}^{T}H{H}^{T}X \end{gathered}$$

上述的H就是中心矩阵，他的作用是使得数据中心化，即
$$H_n^{T}X=\left[\begin{array}{c}(x_1-\overline{x}{)}^T\\ (x_2-\overline{x}{)}^T\\ ......\\ (x_n-\overline{x}{)}^T\end{array}\right]$$

性质如下：

1. H = H ^T
2. Hⁿ = H

PAC

PAC算法的思想总结一句话——将一组可能线性相关的变量通过正交变换变换成一组线性无关的变量，即原始特征重构。
接下来我们从两个角度来看PAC算法，一个是最大投影方差，另一个是最小重构距离。

最大投影方差

如上图有一堆二维分散的数据点，我们选择了u₁和u₂两个方向进行投影，哪个方向效果更好呢？
从图中可以直观看到u₁方向更好，从数学角度看，是因为它的投影矿都d₁远大于d₂，从而造成投影方差更大，即投影后的数据分布更加的分散。
当我们确定了u₁方向投影效果最好时，即找到了主成分。我们来尝试求最大投影方差。

设 || u₁ || = 1，即 u₁^T u₁ = 1，有n个数据点。
一般步骤：

1. 中心化
   $$x_i-\overline{x}$$
2. 求一个点的投影距离
   $$点x_1的投影距离=(x_1-\overline{x}{)}^T{u}_1$$
3. 求所有样本点的投影距离之和
   $$投影长度之和P=\sum _{i=1}^n(x_i-\overline{x}{)}^T{u}_1$$
4. 求投影方差
   $$\begin{gathered} J=\frac{1}{n}\sum _{i=1}^n[(x_i-\overline{x}{)}^T{u}_1{]}^2 \\ =\frac{1}{n}\sum _{i=1}^n((x_i-\overline{x}{)}^T{u}_1{)}^T((x_i-\overline{x}{)}^T{u}_1) \\ =\frac{1}{n}\sum _{i=1}^n{u}_1^T(x_i-\overline{x})(x_i-\overline{x}{)}^T{u}_1 \\ =u_1^T(\frac{1}{n}\sum _{i=1}^n(x_i-\overline{x})(x_i-\overline{x}{)}^T)u_1 \\ 根据式(6)可得： \\ J=u_1^{T}S{u}_1\text{\hspace{1em}(7)} \end{gathered}$$
5. 求最大投影方差

求maxJ，且u₁^T u₁ = 1，根据拉格朗日乘子法可得：
$$L(u_1,\lambda )=u_1^{T}S{u}_1+\lambda (1-u_1^T{u}_1)$$
$$\begin{gathered} \frac{\partial L}{\partial u_1}=2S{u}_1-2\lambda u_1=0 \\ 所以可得： \\ S{u}_1=\lambda u_1\text{\hspace{1em}(8)} \end{gathered}$$

通过观察式（8），可以发现这是一个特征值分解，即$\lambda$是协方差矩阵S的特征值，u₁是于特征值对应的特征向量。PCA的方法就是选择前k个最大特征值对应的特征向量，然后变成单位向量，即选取了k个主成分进行降维。

最小重构距离

实际上是比较n维数据点用另一个n维坐标轴映射，然后从n维挑选p个坐标轴映射的数据前后的误差。
下图原始数据点x是一个二维向量，通过u1和u2两个方向映射成一个新的同维度的数据点x’，很明显向量坐标将会改变，且新的x’ = (x^Tu1)u1 + (x^Tu2)u2

同样对于n个样本的p维向量x_i，我们假设中心化后映射到向量u₁、u₂、…、u_n。则新的向量：
$$x_i^{\prime }=\sum _{k=1}^p((x_i-\overline{x}{)}^T{u}_k)u_k$$
如果我们要从原先的p维降到q维，则映射后的向量为：
$$x_i=\sum _{k=1}^q((x_i-\overline{x}{)}^T{u}_k)u_k$$
设重构误差为J，则：
$$\begin{gathered} J=\frac{1}{n}\sum _{i=1}^n||x_i-x_i|{|}^2=\frac{1}{n}\sum _{i=1}^n||\sum _{k=q+1}^p((x_i-\overline{x}{)}^T{u}_k)u_k|{|}^2 \\ =\frac{1}{n}\sum _{i=1}^n\sum _{k=q+1}^p((x_i-\overline{x}{)}^T{u}_k{)}^2 \\ =\sum _{k=q+1}^p{u}_k^{T}S{u}_k \end{gathered}$$

同理对J进行拉格朗日乘子法，得
$$L(u_k,\lambda )=\sum _{k=q+1}^p{u}_k^{T}S{u}_k+\sum _{k=q+1}^p\lambda (1-u_k^T{u}_k)$$
$$\begin{gathered} \frac{\partial L}{\partial u_k}=\sum _{k=q+1}^{p}2S{u}_1-\sum _{k=q+1}^{p}2\lambda u_1=0 \\ 所以可得： \\ \sum _{k=q+1}^{p}S{u}_1=\sum _{k=q+1}^p\lambda u_1\text{\hspace{1em}(9)} \end{gathered}$$
$$\frac{\partial L}{\partial \lambda }=\sum _{k=q+1}^p(1-u_k^T{u}_k)=0\text{\hspace{1em}(10)}$$

将式（9）、（10）带入L函数可得：
$$L=\sum _{k=q+1}^p\lambda$$

因为要使得L最小，所以选择得特征值是从最小得几个里面选择，即从p维降到q维，需要抛弃掉最小得p-q个特征值及其对应的特征向量。

从SVD角度看PAC

方阵S进行特征值分解可得：
$$S_{pp}=V_{pn}{K}_{pp}{V}^T其中V^{T}V=1,且K=\left[\begin{array}{cccc}{\lambda }_1& 0& 0& ...\\ 0& {\lambda }_2& 0& ...\\ ...& ...& ...& ...\\ 0& 0& ...& {\lambda }_p\end{array}\right]\text{\hspace{1em}(11)}$$

接下来对中心化后的原数据进行奇异值分解：
$$HX=U\Lambda V^T且U^{T}U=V^{T}V=E,{\Lambda }^T=\Lambda \text{\hspace{1em}(12)}$$
然后对协方差矩阵S进行分析：
$$S=\frac{1}{n}{X}^{T}H{H}^{T}X=\frac{1}{n}{X}^{T}HX=\frac{1}{n}{X}^T{H}^{T}HX=\frac{1}{n}(HX{)}^{T}HX$$

忽略系数 $\frac{1}{n}$，且将式（12）代入可得：
$$S_p=V\Lambda U^{T}U\Lambda V^T=V{\Lambda }^2{V}^T\text{\hspace{1em}(13)}$$
对比式（11）和式（13），V = V，K = $\Lambda$²，其中V表示各个特征值对应的特征向量，$\Lambda$²存储着对应协方差矩阵S的特征值。

最后我们定义一个方阵T：
$$T_n=HX(HX{)}^T=U\Lambda V^{T}V\Lambda U^T=U{\Lambda }^2{U}^T\text{\hspace{1em}(14)}$$

可以发现S和T有有相同的特征值，但两者作用不大相同。
S分解，得到特征值和特征向量V，然后得到转换后的数据点坐标——（HXV）
T分解，直接得到坐标。

$$\because 坐标=HXV=U\Lambda V^{T}V=U\Lambda$$
$$\therefore T(U\Lambda )=U{\Lambda }^2{U}^{T}U\Lambda =U{\Lambda }^3=(U\Lambda ){\Lambda }^2$$

总结：可以对T分解也可以对S进行分解，二者维度不一样，前者pxp，后者nxn，故应尽量选择维度更低。