数字图像处理 - 实验作业二 - Python

第三章 灰度变换与空间滤波

它的与众不同之处在于，是透过光线看阴影还是透过阴影看亮度

本章主要介绍了一些在空间域对图像进行处理的技术，空间域就是简单的包含图像像素的平面，空间域技术直接在图像像素上操作。

空间域的处理可由下式进行表示
$$g(x,y)=T[f(x,y)]$$

从左至右分别代表处理后的图像、算子、输入图像

图像处理所使用的图像都是可以自行选择和更换的

1、仿真实现一种灰度变换增强图像

灰度变换函数可以理解为一种点对点的映射，即g仅取决于点(x,y)处的f值，为此，我们可以将之前的式子重新表达为
$$s=T(r)$$

其中的变量r与s分别代表原图像和目标图像在任意点的灰度

基本的灰度变换函数包括图像反转，对数变换，幂律（伽马）变换，分段线性变换函数

本节实验使用幂律变换来展示效果，其基本形式为
$$s=c{r}^{\gamma }$$

幂律变换所用到的Python代码为

import matplotlib.pyplot as plt
import matplotlib.image as img
import numpy as np


def gamma_trans(image,c=1,gamma=0.5):
    normalized_image = image / 255
    result = c * np.power(normalized_image, gamma)
    return np.float64(result)


src = img.imread("sun.jpg")
dst = gamma_trans(src)

plt.figure()
plt.imshow(src,vmin=0,vmax=255)
plt.axis("off")
plt.figure()
plt.imshow(dst,vmin=0,vmax=255)
plt.axis("off")
plt.show()

将原图和结果图放在一起比较

从两个图像的对比之中可以看见，桥、树本来在颜色偏暗的情况下都得到了亮度上的提升。可见幂律变换将较窄的暗色输入值映射为较宽范围的输出值，随着γ的值的不同，得到的结果也会相应有所改变。但对于这一张照片来说，最主要的影响观感的因素还是拍摄的角度，光线太强了。

---

2、仿真实现一幅图像的直方图

直方图可以看成是一个离散的函数，其横坐标为灰度值，例如我们常见的灰度图像就有0到255共256个灰度值，纵坐标为像素的个数。

在实践中也经常使用归一化直方图，此时其纵坐标等于原像素的个数除以总像素的个数，即每种灰度值像素出现的概率。归一化直方图的所有分量之和等于1

可以推测，低对比度图像有较窄的的直方图，且集中于灰度级的中部；对于暗图像，直方图分量集中在灰度级的低端；对于亮图像，直方图分量则倾向于灰度级的高端。若一幅图像的像素倾向占据整个可能的灰度级并均匀分布，则该图像会有高对比度的外观并展示灰色调的较大变化

用到的图像还是和上一小节一样，但是已经转化为灰度图像

由于要求，不使用hist直接绘制，采用柱状图绘制，并进行对比验证，其Python代码为

import matplotlib.pyplot as plt
import numpy as np
from PIL import Image


def normalization(data):
    data = data/np.sum(data)
    return data


# 读取图像并转为灰度
src = np.array(Image.open("sun.jpg").convert("L"))
colors = []

# 记录每一个灰度值的像素数
if not colors:
    for i in range(256):
        colors.append(np.sum(src == i))

pixels = [i for i in range(256)]

# 转变为概率分布
c = normalization(colors)
# 减少运算时间
src_for_hist = src.reshape(1, -1).tolist()

plt.figure()
plt.bar(pixels,c)
plt.figure()
plt.hist(src_for_hist, bins=255, density=1)
plt.show()

我们将使用柱状图模拟和直接利用直方图绘制函数的两个结果进行比较

以上用柱状图仿真的结果已进行归一化运算
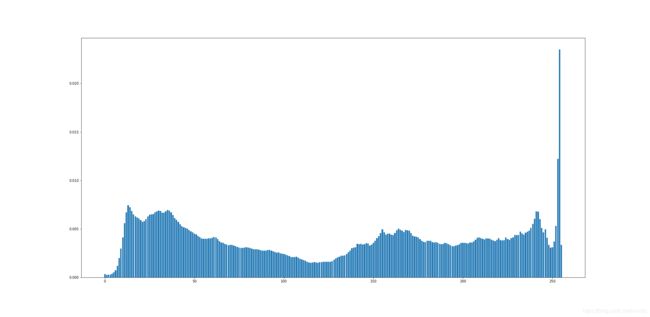
实际利用直方图函数绘制的结果为：

对比以上两图我们可以得出结论，我们所采用的绘制方法是正确，唯一与自带函数不同之处就是直接绘制的直方图连接更为紧密，每个分量之间没有空隙

---

3、仿真实现图像的直方图均衡化处理

直方图均衡化时利用直方图对图像的对比度进行一个调整。其效果就是对于过亮或过暗的图像，其直方图的像素分布的强度都有一个更平滑的调整，从视觉的观感上来说就是有了更高的对比度

直方图均衡化处理的公式为
$$s_k=T(r_k)=(L-1)\sum _{j=0}^k{p}_r(r_j)=\frac{n_k}{MN}\sum _{j=0}^k{n}_j$$

$$k=0,1,2,\dots ,L-1$$

为了便于运算，这里换了一张原图，我们将对新图进行直方图均衡化处理，其相关的代码为

import matplotlib.pyplot as plt
import numpy as np
from PIL import Image

src = np.array(Image.open("equa.jpg").convert("L"))
colors = []

if not colors:
    for i in range(256):
        colors.append(np.sum(src == i))

normalized_colors = colors / np.sum(colors)

h, w = src.shape
dst = np.zeros_like(src)

for i in range(h):
    for j in range(w):
        res = 0
        for k in range(src[i, j]):
            res += normalized_colors[k]
        s = 255 * res
        dst[i][j] = np.round(s)
    if i % 50 == 0:
        print("finish ", i, " line", ",total ", h, " line")

plt.figure()
plt.imshow(src, cmap='gray', vmin=0, vmax=255)
plt.axis("off")
plt.figure()
plt.imshow(dst, cmap='gray', vmin=0, vmax=255)
plt.axis("off")
plt.figure()
plt.hist(src.reshape(1,-1).tolist(),bins=255,density=1)
plt.figure()
plt.hist(dst.reshape(1,-1).tolist(),bins=255,density=1)
plt.show()

原图和直方图均衡化之后的图像分别为

两张图的直方图分布分别为（前一节代码可以绘制直方图）

可见直方图的分布更加的“均匀”，因而其对比度也得到了提高

---

4、仿真实现多幅图像平均去高斯白噪声

高斯白噪声是符合正态分布的一种噪声，首先要做的就是要给实验图像加上高斯白噪声。

但是要实现多幅图像平均的效果，就需要有多幅加了高斯白噪声的图像。本节实验打算生成40幅添加了高斯白噪声的图像，并对这些图像求平均，来观察最终结果。

简单来说，多幅图像平均去高斯白噪声就是用很多张都被高斯白噪声污染的图像进行求平均运算，得到无高斯白噪声的图像。

高斯白噪声对于图像的影响如下所示，图片是随便从网上找的，已转化为灰度图像

这里我们还需要总共产生40张的具有高斯白噪声的实验图，如下所示

对40张图片求平均之后得到的最终效果为

可以看出这个方法成功的去除了图像中的高斯噪声，但是也可以看出灰度级的颜色上相比较原来的图像变少了，可见还是受了噪声的影响，要完全去除可能需要更多的加了高斯噪声的图片。但是这里多幅度平均去噪声的方法得到验证

整个过程实现的Python代码如下所示

import matplotlib.pyplot as plt
import numpy as np
from PIL import Image

src = np.array(Image.open("gao.jpg").convert("L"))
plt.figure()
plt.imshow(src, cmap="gray")
plt.axis("off")

# normalization
normalized_img = src / 255
noise = np.random.normal(size=normalized_img.shape) * 0.1

noised_img = normalized_img + noise # add noise
plt.figure()
plt.imshow(noised_img, cmap="gray")
plt.axis("off")

dst = np.zeros_like(src, dtype='float64')
noised_img_list = []

for i in range(40):
    noise = np.random.normal(size=normalized_img.shape) * 0.1
    noised_img = normalized_img + noise
    noised_img_list.append(noised_img)
    dst += noised_img

dst = dst / 40
plt.figure()
plt.imshow(dst, cmap="gray")
plt.axis("off")

_, fig = plt.subplots(5, 8, figsize=(12, 18))
# set figure size
plt.subplots_adjust(top=0.985, bottom=0.015, left=0.013, right=0.987, hspace=0.0, wspace=0.113)

for i in range(5):
    for j in range(8):
        fig[i][j].imshow(noised_img_list[i + j], cmap="gray")
        fig[i][j].axis("off")

plt.show()

---

5、仿真实现均值滤波去除高斯白噪声

均值滤波是典型的线性滤波算法，它是指在图像上对目标像素给一个模板，该模板包括了其周围的临近像素（以目标像素为中心的周围8个像素，构成一个滤波模板，即去掉目标像素本身），再用模板中的全体像素的平均值来代替原来像素值。

我们要做的就是在加了高斯白噪声的图像上，从左到右，从上到下，依次选取3*3共9个像素，并对9个像素求平均值，把值赋给中心的值。

简单来说就是有一幅加了高斯白噪声的图像，然后我要对像素值进行修正，对于每一个像素点修正的方法就是把它周围的8个点加进来组成一个3*3的矩阵然后求均值，赋给刚刚那个像素点。

均值滤波的效果如下所示，分别是加了高斯噪声的图和均值滤波后的图

注意：滤波前要先填充边缘

实现的代码如下所示：

import matplotlib.pyplot as plt
import numpy as np
from PIL import Image

src = np.array(Image.open("gao.jpg").convert("L"))
plt.figure()
plt.imshow(src, cmap="gray")
plt.axis("off")

normalized_img = src / 255
noise = np.random.normal(size=normalized_img.shape) * 0.1

noised_img = normalized_img + noise
plt.figure()
plt.imshow(noised_img, cmap="gray")
plt.axis("off")


def mean_filter(src_img):
    kernel_size = 3
    fill = int((kernel_size - 1) / 2)
    padded_img = np.pad(src_img, fill, 'constant')
    height, width = src_img.shape
    mean_img = np.zeros_like(src_img, dtype="float64")

    for i in range(height):
        for j in range(width):
            corr = padded_img[i:i + kernel_size, j:j + kernel_size]
            mean_img[i, j] = np.mean(corr)

    return mean_img


dst = mean_filter(noised_img)
plt.figure()
plt.imshow(dst, cmap="gray")
plt.axis("off")
plt.show()

可见，均值滤波对于去除图像中的高斯噪声有一定的作用，但是均值滤波本身存在着固有的缺陷，即它不能很好地保护图像细节，在图像去噪的同时也破坏了图像的细节部分，从而使图像变得模糊，不能很好地去除噪声点。

---

6、仿真实现中值滤波去除噪声

椒盐噪声也称为脉冲噪声，是图像中经常见到的一种噪声，它是一种随机出现的白点或者黑点，可能是亮的区域有黑色像素或是在暗的区域有白色像素（或是两者皆有）。

椒盐噪声的成因可能是影像讯号受到突如其来的强烈干扰而产生、类比数位转换器或位元传输错误等。例如失效的感应器导致像素值为最小值，饱和的感应器导致像素值为最大值。

中值滤波的原理同均值滤波相似，但不是取均值，还是取中值

首先要在图像上加上椒盐噪声，然后用中值滤波去除，滤波前要先填充边缘。含有椒盐噪声的图像和去除噪声后的图像如下所示，使用的原图像还是和第四小节中的一样

可见对于椒盐噪声，中值滤波的方法还是具有一定的效果的，但是看到去除的效果还不是很完全，这里估计应该是需要更加高的强度来去除。但是中值滤波去噪声的方式得到了验证。

实现的代码如下所示

import matplotlib.pyplot as plt
import numpy as np
from PIL import Image

src = np.array(Image.open("gao.jpg").convert("L"))
plt.figure()
plt.imshow(src, cmap="gray")
plt.axis("off")


def salt(image, prob):
    """噪声比例prob"""
    output = np.zeros(image.shape, np.uint8)
    thres = 1 - prob
    for i in range(image.shape[0]):
        for j in range(image.shape[1]):
            rdn = np.random.random()
            if rdn < prob:
                output[i][j] = 0
            elif rdn > thres:
                output[i][j] = 255
            else:
                output[i][j] = image[i][j]
    return output


noise = salt(src, 0.2)
plt.figure()
plt.imshow(noise, cmap="gray")
plt.axis("off")


def median_filter(src_img):
    kernel_size = 3
    fill = int((kernel_size - 1) / 2)
    img = np.pad(src_img, fill, 'constant')
    height, width = src_img.shape
    arr = np.zeros_like(src_img, dtype="float64")

    for i in range(height):
        for j in range(width):
            corr = img[i:i + kernel_size, j:j + kernel_size]
            arr[i, j] = np.median(corr)

    return arr


dst = median_filter(noise)
plt.figure()
plt.imshow(dst, cmap="gray")
plt.axis("off")
plt.show()

可以看出中值滤波的确能够有效地去除椒盐噪声，但是由于我选取的中值滤波的模板的问题，依然有部分噪声残余，但是依然能够很明显的看出，中值滤波对于去除脉冲噪声有着很明显的作用。

---

7、分别用Laplace算子和sobel算子实现图像的锐化增强

首先，这两个算子的结构和前面的均值模板、中值模板类似，也是一个3x3的结构，但这次并不只是选取了原图像中的3x3矩阵，两个算子分别定义了3x3的矩阵，并将原图像获得的矩阵和这个矩阵做相关运算，相关运算的意思可以理解为对应的位置相乘，然后求和，后续步骤一样。

Laplace算子作为边缘检测的方法之一，也是工程数学中常用的一种积分变换。把图像的像素值想象成一个变化的曲线。对应变化的曲线，一阶导数的极值位置，二阶导数为0，利用这个来检测边缘。具体的原理可以参考教材《数字图像处理》

sobel算子是计算机视觉领域的一种重要处理方法。主要用于获得数字图像的一阶梯度，常见的应用和物理意义是边缘检测。索贝尔算子是把图像中每个像素的上下左右四领域的灰度值加权差，在边缘处达到极值从而检测边缘。具体原理见教材

反应到我们处理的过程，就是要按照3*3依次从图像左到右，上到下选取矩阵，与算子相乘，赋值给中心元素。处理前要先填充边缘，其中soble算子分为水平和垂直两种

首先，通过Laplace算子处理过的图像为

从图中可以看出，图像的相较于原来的图像更加锐利了，好像有用铅笔勾勒的效果一般，但是感觉整体的灰度等级范围缩小了，颜色似乎更加接近了一下。但是通过拉普拉斯算子锐化出来的图像还是很好看的。

以下是索贝尔算子的处理结果，分别为水平与垂直两种

索贝尔算子水平锐化：

索贝尔算子垂直锐化：

从图中可以看出在两章图片中，索贝尔算子水平和垂直两种边缘各有侧重，验证了方法的正确。

相关实现的代码如下所示

import matplotlib.pyplot as plt
import numpy as np
from PIL import Image

src = np.array(Image.open("gao.jpg").convert("L"))
plt.figure()
plt.imshow(src, cmap="gray")
plt.axis("off")


def laplace(img, c):
    """
    拉普拉斯锐化图像
        输入图像src
        锐化系数para
    """
    kernel = 3
    lap_filter = np.array([[1, 1, 1],
                           [1, -8, 1],
                           [1, 1, 1]])

    fill = int((kernel - 1) / 2)
    padded_img = np.pad(img, fill, 'constant')
    height, width = img.shape
    arr = np.zeros_like(img, dtype="float64")

    for i in range(height):
        for j in range(width):
            corr = padded_img[i:i + kernel, j:j + kernel]
            r = np.sum(np.dot(lap_filter,corr))
            arr[i, j] = padded_img[i, j] + c * r

    return arr


dst_h = laplace(src, -0.2)
plt.figure()
plt.imshow(dst_h, cmap="gray")
plt.axis("off")


def sobel_h(src, c, kernel=3):
    sobel_filter = np.array([[-1, -2, -1],
                             [0, 0, 0],
                             [1, 2, 1], ])

    fill = int((kernel - 1) / 2)
    img = np.pad(src, fill, 'constant')
    height, width = src.shape
    arr = np.zeros_like(src, dtype="float64")

    for i in range(height):
        for j in range(width):
            corr = img[i:i + kernel, j:j + kernel]
            R = np.sum(sobel_filter * corr)
            arr[i, j] = src[i, j] + c * R

    return arr


dst = sobel_h(src, 1)
plt.figure()
plt.imshow(dst, cmap="gray")
plt.axis("off")


def sobel_v(src, c, kernel=3):
    sobel_filter = np.array([[-1, 0, 1],
                             [-2, 0, 2],
                             [-1, 0, 1], ])

    fill = int((kernel - 1) / 2)
    img = np.pad(src, fill, 'constant')
    height, width = src.shape
    arr = np.zeros_like(src, dtype="float64")

    for i in range(height):
        for j in range(width):
            corr = img[i:i + kernel, j:j + kernel]
            R = np.sum(sobel_filter * corr)
            arr[i, j] = src[i, j] + c * R

    return arr


dst_v = sobel_v(src, 1)
plt.figure()
plt.imshow(dst_v, cmap="gray")
plt.axis("off")
plt.show()