关于Java的Hash算法的深入理解

我们眼中的哈希

在计算机领域中哈希涉及的范围非常广泛，而且是较长使用的一种算法和数据结构，对此我们在后端开发中不断地使用由jdk提供的方法进行使用。由于长时间的使用，很少人会去对里面的核心进行分析和学习。HashMap是通过一个Entry的数组实现的。而Entry的结构有三个属性，key，value，next。如果在c中，我们遇到next想到的必然是指针，其实在java这就是个指针。每次通过hashcode的值，来散列存储数据。今天就来看下那些对于一个专业的开发者而言必要了解的东西。

引用一句百度对于哈希算法的定义：哈希算法可以将任意长度的二进制值引用为较短的且固定长度的二进制值，把这个小的二进制值称为哈希值。

一、HashMap

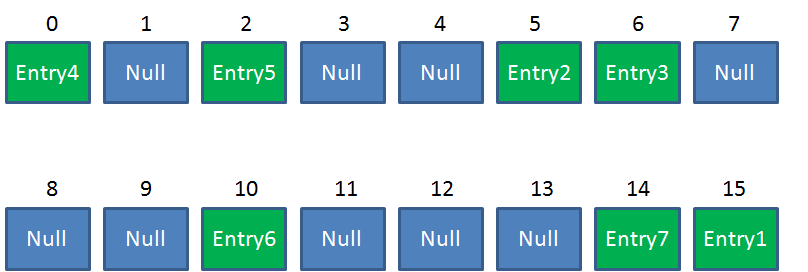
HashMap是一个用于存储Key-Value键值对的集合，每一个键值对也叫做Entry。这些个键值对（Entry）分散存储在一个数组当中，这个数组就是HashMap的主干。HashMap数组每一个元素的初始值都是Null。

HashMap的默认初始长度？为什么?

HashMap的初始化长度是16，负载因子是0.75，并且每次自动扩展或是手动初始化时，长度必须是2的幂。之所以选择16，是因为有效提供给key映射到index的Hash算法。从Key映射到HashMap数组的对应位置，会用到一个Hash函数。利用Key的HashCode值来做某种运算来达到一种尽可能均匀分布的Hash函数，这种算法采用的是位运算的方式实现,这也是初始化长度为16的另一个原因，使用16的长度可以比其他相对范围内的数值运算后出现的数更独立，减少了同一个数值出现的次数，实现了更均匀的结果。

如何进行位运算呢？有如下的公式（Length是HashMap的长度）：

index = HashCode（Key） & （Length - 1）

下面我们以值为“book”的Key来演示整个过程：

1.计算book的hashcode，结果为十进制的3029737，二进制的101110001110101110 1001。

2.假定HashMap长度是默认的16，计算Length-1的结果为十进制的15，二进制的1111。

3.把以上两个结果做与运算，101110001110101110 1001 & 1111 = 1001，十进制是9，所以 index=9。

可以说，Hash算法最终得到的index结果，完全取决于Key的Hashcode值的最后几位。

假设HashMap的长度是10，重复刚才的运算步骤：

HashCode：10 1110 0011 1010 1110 1001
Length-1：1001
Index：   1001

单独看这个结果，表面上并没有问题。我们再来尝试一个新的HashCode 101110001110101110 1011 ：

HashCode：10 1110 0011 1010 1110 1011
Length-1：1001
Index：   1001

让我们再换一个HashCode 101110001110101110 1111 试试 ：

HashCode：10 1110 0011 1010 1110 1111
Length-1：1001
Index：   1001

是的，虽然HashCode的倒数第二第三位从0变成了1，但是运算的结果都是1001。也就是说，当HashMap长度为10的时候，有些index结果的出现几率会更大，而有些index结果永远不会出现（比如0111）！

这样，显然不符合Hash算法均匀分布的原则。

反观长度16或者其他2的幂，Length-1的值是所有二进制位全为1，这种情况下，index的结果等同于HashCode后几位的值。只要输入的HashCode本身分布均匀，Hash算法的结果就是均匀的。

---

高并发下的HashMap

在高并发下使用HashMap，它的容量是有限的，所以HashMap会通过ReHash的方式进行扩容，使用ReHash能够使容量扩大本身的两倍。所以ReHash是在HashMap扩容时的一个步骤。当经过多次元素插入，使得HashMap达到一定的饱和度，key映射位置发生冲突的几率会逐渐增高。这个情况我们需要进行Resize，那么影响Resize的因素有两个：Capacity 初始长度 、LoadFactor 负载因子.

HashMap.Size >= Capacity * LoadFactor

HashMap的Resize经过两个步骤：

1. 扩容：创建一个新的Entry空数组，长度是原来的两倍
2. ReHash：遍历原来的Entry数组，把所有的Entry重新Hash到新数组。因为长度扩大之后Hash的规则会发生变动，因此需要重新Hash。

回顾一下Hash公式： index = HashCode（Key） & （Length - 1）

当原数组长度为8时，Hash运算是和111B做与运算；新数组长度为16，Hash运算是和1111B做与运算。Hash结果显然不同。

Resize前的HashMap：

Resize后的HashMap：

ReHash的Java代码如下：

/**
 * Transfers all entries from current table to newTable.
 */
void transfer(Entry[] newTable, boolean rehash) {
    int newCapacity = newTable.length;
    for (Entry e : table) {
        while(null != e) {
            Entry next = e.next;
            if (rehash) {
                e.hash = null == e.key ? 0 : hash(e.key);
            }
            int i = indexFor(e.hash, newCapacity);
            e.next = newTable[i];
            newTable[i] = e;
            e = next;
        }
    }
}

HashMap线程问题（参考JDK1.7）

上面的情况使用在单线程下是没有问题的，但是一旦使用在多线程中，那么就会出现破坏内部数据结构的链表数组。其中一些链接可能会丢失，或者形成了回路，从而导致数据结构不可用。在ConcurrentHashMap中是不会发生的,高并发的情况下使用这个集合类兼顾了线程安全和性能。为保证线程安全可以使用HashTable、collections、synchronizedMap。

内容包括:

1. Hashmap在插入元素过多的时候需要进行Resize，Resize的条件是
   HashMap.Size >= Capacity * LoadFactor。

2. Hashmap的Resize包含扩容和ReHash两个步骤，ReHash在并发的情况下可能会形成链表环。

原理：

假设一个HashMap已经到了Resize的临界点。此时有两个线程A和B，在同一时刻对HashMap进行Put操作：

此时达到Resize条件，两个线程各自进行Rezie的第一步，也就是扩容：

这时候，两个线程都走到了ReHash的步骤。让我们回顾一下ReHash的代码：

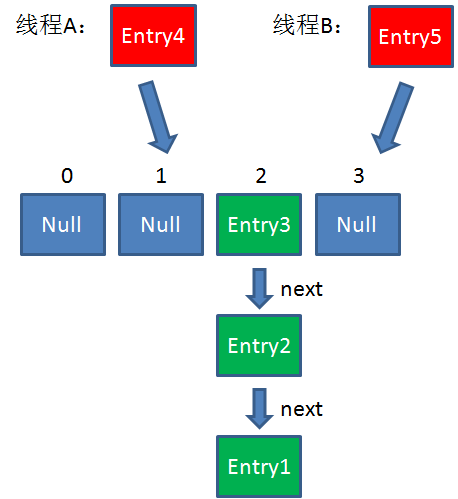
假如此时线程B遍历到Entry3对象，刚执行完红框里的这行代码，线程就被挂起。对于线程B来说：

e = Entry3
next = Entry2

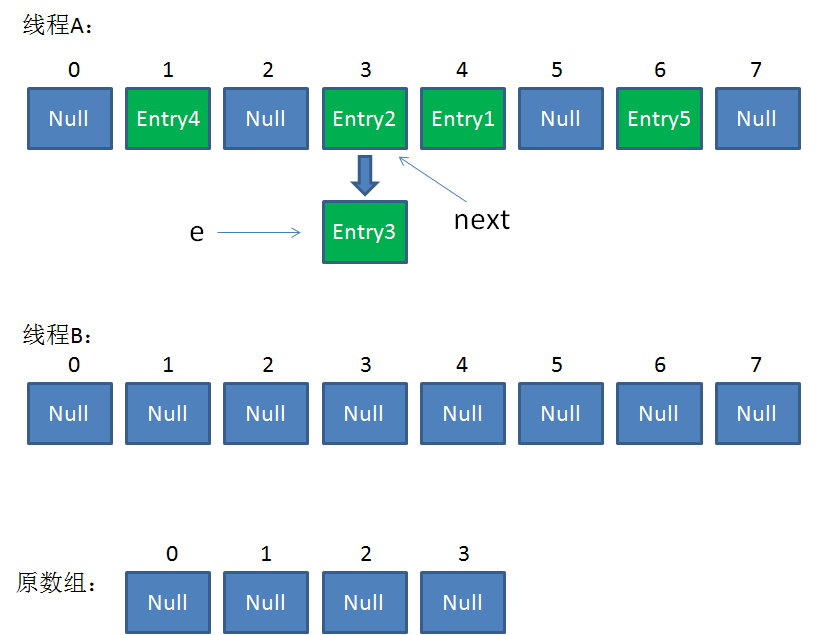
这时候线程A畅通无阻地进行着Rehash，当ReHash完成后，结果如下（图中的e和next，代表线程B的两个引用）：

直到这一步，看起来没什么毛病。接下来线程B恢复，继续执行属于它自己的ReHash。线程B刚才的状态是：

e = Entry3
next = Entry2

当执行到上面这一行时，显然 i = 3，因为刚才线程A对于Entry3的hash结果也是3。

我们继续执行到这两行，Entry3放入了线程B的数组下标为3的位置，并且e指向了Entry2。此时e和next的指向如下：

e = Entry2
next = Entry2

整体情况如图所示：

接着是新一轮循环，又执行到红框内的代码行：

e = Entry2
next = Entry3

整体情况如图所示：

接下来执行下面的三行，用头插法把Entry2插入到了线程B的数组的头结点：

整体情况如图所示：

第三次循环开始，又执行到红框的代码：

e = Entry3
next = Entry3.next = null

最后一步，当我们执行下面这一行的时候，见证奇迹的时刻来临了：

newTable[i] = Entry2
e = Entry3
Entry2.next = Entry3
Entry3.next = Entry2

链表出现了环形！

整体情况如图所示：

此时，问题还没有直接产生。当调用Get查找一个不存在的Key，而这个Key的Hash结果恰好等于3的时候，由于位置3带有环形链表，所以程序将会进入死循环！

---

ConcurrentHashMap的出现确保了线程的安全且高效率

1. 这里介绍的ConcurrentHashMap原理和代码，都是基于Java1.7的。在Java8中会有些许差别。
2. ConcurrentHashMap在对Key求Hash值的时候，为了实现Segment均匀分布，进行了两次Hash。有兴趣的朋友可以研究一下源代码。

---

String中的HashCode（）

String类有个私有的实例字段hash表示这串哈希值，第一次调用的时候，字符串的哈希值会被计算并且赋值给Hash字段，之后再调用HashCode的方法直接取hash字段返回。算法中的方式是，以31为乘法算式中的因数，再和每个字符进行ASCII码对应值作运算。

public int hashCode() {
    int h = hash;
    if (h == 0 && value.length > 0) {
        char val[] = value;

        for (int i = 0; i < value.length; i++) {
            h = 31 * h + val[i];
        }
        hash = h;
    }
    return h;
}

字符串哈希可以做很多事情，通常是类似于字符串判等，判回文之类的。

但是仅仅依赖于哈希值来判断其实是不严谨的，除非能够保证不会有哈希冲突，通常这一点很难做到。

就拿jdk中String类的哈希方法来举例，字符串”gdejicbegh”与字符串”hgebcijedg”具有相同的hashCode()返回值-801038016，并且它们具有reverse的关系。这个例子说明了用jdk中默认的hashCode方法判断字符串相等或者字符串回文，都存在反例。

---

部分的原理来自数据算法与数据结构和程序员小灰的文章观点，针对某些原理本人进行一些个人的理解，大部分自己进行了深入的理解和探索。对某些问题进行了许多补充。学习是我们开始研究并且进行创造的基本需要，我们引用学习并且使用这些基础进行延伸的创造和提供价值，这是我们人类历史上进化的必需过程。