python绘制柱状图，如何改变柱状柱间距，如何设置横纵轴标签（绘制Intel Realsense D435深度误差柱状图）

参考文章1：Python 绘制 柱状图

# 创建一个点数为 8 x 6 的窗口, 并设置分辨率为 80像素/每英寸
plt.figure(figsize=(10, 10), dpi=80)
# 再创建一个规格为 1 x 1 的子图
# plt.subplot(1, 1, 1)
# 柱子总数
N = 10
# 包含每个柱子对应值的序列
values = (56796,42996,24872,13849,8609,5331,1971,554,169,26)
# 包含每个柱子下标的序列
index = np.arange(N)
# 柱子的宽度
width = 0.45
# 绘制柱状图, 每根柱子的颜色为紫罗兰色
p2 = plt.bar(index, values, width, label="num", color="#87CEFA")
# 设置横轴标签
plt.xlabel('clusters')
# 设置纵轴标签
plt.ylabel('number of reviews')
# 添加标题
plt.title('Cluster Distribution')
# 添加纵横轴的刻度
plt.xticks(index, ('mentioned1cluster', 'mentioned2cluster', 'mentioned3cluster', 'mentioned4cluster', 'mentioned5cluster', 'mentioned6cluster', 'mentioned7cluster', 'mentioned8cluster', 'mentioned9cluster', 'mentioned10cluster'))
# plt.yticks(np.arange(0, 10000, 10))
# 添加图例
plt.legend(loc="upper right")
plt.show()

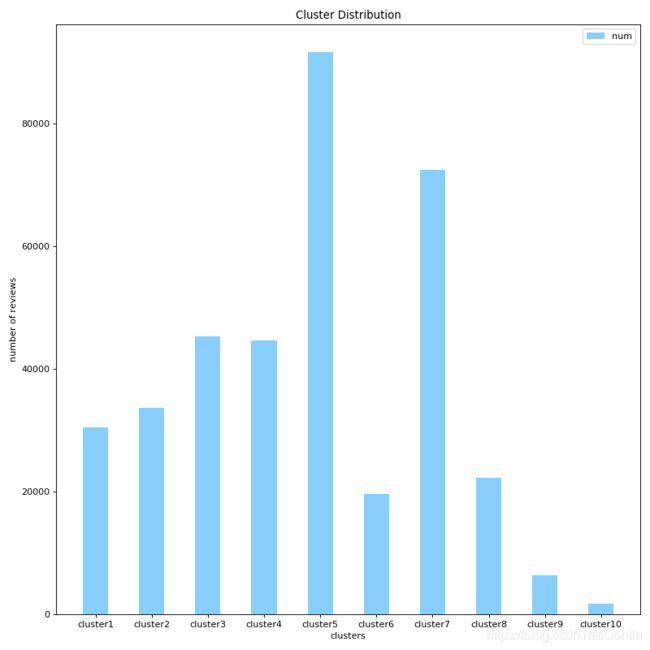
我的代码

# -*- coding: utf-8 -*-
"""
@File    : 测试拟合平面.py
@Time    : 2020/9/8 9:23
@Author  : Dontla
@Email   : [email protected]
@Software: PyCharm
"""
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from numba import jit


# 加载数据
def load_data(file_path):
    # 读取数据
    npzfile = np.load(file_path)
    # x, y, z = npzfile['arr_0'], npzfile['arr_1'], npzfile['arr_2']
    return npzfile['x'], npzfile['y'], npzfile['z']


# 计算拟合片面
def cal_flat(x_, y_, z_):
    # 取样点数量
    point_num = len(x_)
    print('len={}'.format(point_num))

    # 创建系数矩阵A
    a = 0
    A = np.ones((point_num, 3))
    for i in range(0, point_num):
        A[i, 0] = x_[a]
        A[i, 1] = y_[a]
        a = a + 1
    # print(A)

    # 创建矩阵b
    b = np.zeros((point_num, 1))
    a = 0
    for i in range(0, point_num):
        b[i, 0] = z_[a]
        a = a + 1
    # print(b)

    # 通过X=(AT*A)-1*AT*b直接求解
    A_T = A.T
    A1 = np.dot(A_T, A)
    A2 = np.linalg.inv(A1)
    A3 = np.dot(A2, A_T)
    X = np.dot(A3, b)
    print('平面拟合结果为：z = %.6f * x + %.6f * y + %.6f' % (X[0, 0], X[1, 0], X[2, 0]))

    # 计算方差
    R = 0
    for i in range(0, point_num):
        R = R + (X[0, 0] * x_[i] + X[1, 0] * y_[i] + X[2, 0] - z_[i]) ** 2
    print('方差为：%.*f' % (3, R))
    return X


# 绘制三维深度散点图及拟合平面
def show_flat(X):
    # 展示图像
    fig1 = plt.figure()
    ax1 = fig1.add_subplot(111, projection='3d')
    ax1.set_xlabel("x")
    ax1.set_ylabel("y")
    ax1.set_zlabel("z")
    # ax1.scatter(x, y, z, c='r', marker='o')
    ax1.scatter(x, y, z, c='r', marker='.')
    x_p = np.linspace(-200, 1480, 168)
    y_p = np.linspace(-200, 920, 112)
    x_p, y_p = np.meshgrid(x_p, y_p)
    z_p = X[0, 0] * x_p + X[1, 0] * y_p + X[2, 0]
    ax1.plot_wireframe(x_p, y_p, z_p, rstride=10, cstride=10)
    plt.show()


# 计算深度误差
def cal_error_distribution(x_, y_, z_, coefficient_):
    # 计算误差
    error = z_ - (coefficient_[0, 0] * x_ + coefficient_[1, 0] * y_ + coefficient_[2, 0])
    return error


# 统计各个区间误差的数量
def count_error_number(depth_error_, column_num):
    # 提取负向最大深度误差和正向最大深度误差
    error_max = np.max(depth_error)
    # print(error_max)    # 23.39967553034205
    error_min = np.min(depth_error)
    # print(error_min)  # -18.65760653439031

    # 柱子宽度
    error_width = (error_max - error_min) / column_num
    # print(column_width) # 1.6822912825892944

    # 创建柱子高度序列
    column_height_sequence = np.zeros(column_num)

    # 统计每个柱子包含深度点的数量
    for error in depth_error_:
        index = int((error - error_min) // error_width)
        # 当深度误差error等于最大深度误差的时候，下标会溢出，所以要加个判断限制一下
        if index == column_num:
            # print(dep)  # 23.39967553034205
            index -= 1
        column_height_sequence[index] += 1
    # print(column_height_sequence)
    return column_height_sequence


# 绘制柱状图
def draw_histogram(column_height_sequence_):
    # 创建一个点数为 8 x 6 的窗口, 并设置分辨率为 80像素/每英寸
    plt.figure(figsize=(10, 10), dpi=80)
    # plt.figure()
    # 再创建一个规格为 1 x 1 的子图
    # plt.subplot(1, 1, 1)
    # 柱子总数
    N = len(column_height_sequence)
    # 包含每个柱子对应值的序列
    values = column_height_sequence_
    # 包含每个柱子下标的序列
    index = np.arange(N)
    # 柱子的宽度
    width = 1
    # 绘制柱状图, 每根柱子的颜色为紫罗兰色
    # p2 = plt.bar(index, values, width, label="num", color="#87CEFA")
    p2 = plt.bar(index, values, width, label="num", color="#87CEFA")
    # 设置横轴标签
    plt.xlabel('error/mm')
    # 设置纵轴标签
    plt.ylabel('number of points')
    # 添加标题
    plt.title('D435 error Distribution(500mm)')
    # 添加纵横轴的刻度
    index_new = []
    for index_ in index:
        if index_ % 100 == 0:
            index_new.append(index_)
    # print(index_new)
    index_new_content = []
    for index in index_new:
        error_max = np.max(depth_error)
        error_min = np.min(depth_error)
        index_new_content.append(error_min + (error_max - error_min) * index / N)
    index_new_content_string = [str(i) for i in np.around(index_new_content, decimals=1)]
    # plt.xticks(index, (
    #     'mentioned1cluster', 'mentioned2cluster', 'mentioned3cluster', 'mentioned4cluster', 'mentioned5cluster',
    #     'mentioned6cluster', 'mentioned7cluster', 'mentioned8cluster', 'mentioned9cluster', 'mentioned10cluster'))
    plt.xticks(index_new, index_new_content_string)
    # plt.yticks(np.arange(0, 10000, 10))
    # 添加图例
    plt.legend(loc="upper right")
    plt.show()


if __name__ == '__main__':
    # 加载数据
    x, y, z = load_data('./data/500mm/4_1599623292.4111953.npz')

    # 拟合平面并返回平面函数系数
    coefficient = cal_flat(x, y, z)

    # 绘制平面及深度散点
    # show_flat(coefficient)

    # 计算深度误差
    depth_error = cal_error_distribution(x, y, z, coefficient)

    # 统计各个误差区间的数量（柱状图各个柱子高度）
    column_height_sequence = count_error_number(depth_error, 1000)

    # 绘制柱状图
    draw_histogram(column_height_sequence)

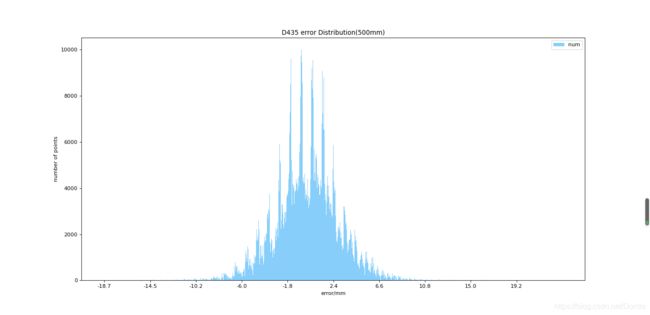
代码中深度数据：
https://download.csdn.net/download/Dontla/12833241