MFC计算器制作----代码实现

MFC计算器制作----代码实现

还没有进行界面设计的朋友可以先看这里：
MFC计算器制作----界面设计

现在界面设计已经接近完成，那么我们将开始实现计算器的所有功能。

1.基础思想

由于计算器包含括号的功能，所以在实现功能上使用了栈的思想。在栈的使用上，建立了两个栈来分别用来储存数字（opnd）和符号（optr）。在计算方法的使用上，采用了中缀式(infix)转为后缀式(postfix)再计算的方法，该方法可以在运算的时候将括号去掉，而且不用再考虑优先级问题；即将运算符放在两个运算对象的后面，按照运算符出现的顺序，从左往右进行计算。这种方法比起中缀式直接计算，多了转换的步骤，但是在总体功能的实现上，后缀式的方法更为简便。
c++的栈库使用可以参考该文章：C++基础：C++标准库之栈（stack）和队列（queue）

2.中缀式转后缀式

用户输入的每一个数字和符号都会储存在一个名为infix的字符数组中，直到用户按下等号为止，该字符数组的所有元素的总和即为我们平时写的计算式，也成为中缀式(1+1=2就是中缀表达式)。

infix[a++]='1' //在用户按下按钮时就会在数组里面增加相应的符号

在用户按下等号键后，程序就会调用中缀转后缀（infix_to_postfix）函数。在转换过程中，如果infix中的元素是数字，这直接转移到postfix数组中；如果infix中的元素是运算符，则进行优先级的比较，从而决定将符号放进符号栈中还是直接放入postfix数组中。
在转换过程中，每一部分会用一个空号隔开，即数字与数字之间，符号与数字之间用空号隔开，从而使程序能分辨出每一个部分。整个过程为一个循环，直到infix的元素为‘\0’。

3.运算符优先级比较

在中缀式转后缀式的过程中，涉及运算符在栈外和栈内的优先级的比较，在该程序中各符号的优先级如下：

运算符	=	(	* / %	+ -	)
栈内优先级	0	1	5	3	6
栈外优先级	0	6	4	2	1

在中缀转后缀的过程中会比较该符号与栈顶元素的优先级，即调用相应函数（程序中分别为priorInStack和priorOutStack函数来提供栈内栈为优先级对应的数字，该函数由一个switch来判断符号对应的数字）来比较数字大小。在比较完数字大小后会进行如下操作之一：

（1） 若infix中的元素数字大于栈顶元素数字，即infix中的元素优先级大于栈顶元素优先级，则将infix中的元素压入符号栈中。
（2） 若infix中的元素数字小于栈顶元素的数字，即infix中的元素优先级小于栈顶元素优先级，则弹出符号栈的栈顶运算符，存入到postfix数组中，infix的元素继续与新栈顶元素进行比较。
（3） 若infix元素是“（”，则直接压入符号栈中
（4） 若infix元素是“）”，则将栈中元素一次存入postfix中，直到遇到“（”，然后“（”退栈，消掉一对括号。
（5） 若infix元素是“=”，开始执行退栈操作，将退栈元素直接存入postfix中，直到栈空，最后在postfix中存入’\0’作为结束标志。

其实现代码如下：

switch (precede(item,infix[i]))//比较运算符优先级
           {
                 case -1://栈外优先级高于栈内优先级
                          optr.push(infix[i]);
                          i++;
                          break；
                 case 0://如果是等号或者括号的时
                      item= optr.top();
                      optr.pop();
                      if (item != '=') i++;
                      break;
                 case 1://如果栈内优先级高于栈外
                      item= optr.top();
                      optr.pop();
                      postfix[j++]= item;
            }

precede(char item, char ch)//比较优先级
{
 if (priorInStack(item) < priorOutStack(ch)) return -1;
 else if (priorInStack(item) == priorOutStack(ch)) return 0;
 else return 1;
}

priorInStack(char item)//栈内优先级
{
 int in;
 switch(item) {
  case '=':
   in = 0;
   break;
  case '(':
   in = 1;
   break;
  case 'm'://取余
  case '*':
  case '/':
   in = 5;
   break;
  case '+':
  case '-':
   in = 3;
   break;
  case')':
   in = 6;

priorOutStack(char ch)//栈外优先级
{
 int out;
 switch (ch) {
     case '=':
   out = 0;
   break;
  case '(':
   out = 6;
   break;
  case 'm':
  case '*':
  case '/':
   out = 4;
   break;
  case '+':
  case '-':
   out = 2;
   break;
  case ')':
   out = 1;
   break;

4.后缀式计算

在转换完后缀式之后，程序会调用后缀式计算（calculate）函数;整个函数就是一个循环，一直循环到postfix为‘\0’。如果postfix数组元素是数字或者小数点，则将其转换为数字压入到数字栈中；如果postfix数组元素是运算符则分为两种情况：（1）如果运算符是加、减、乘、除、取余、乘方，则从数字栈中弹出两个数字进行相应的操作。（2）如果运算符是三角函数、反三角函数、对数函数及阶乘，则只从数字栈中弹出一个数字进行相应的操作。

在进行相应操作后，得到的数字会压入数字栈中，循环继续进行，直到postfix为‘\0’；此时数字栈中只剩下一个数字，则该数字则为后缀式计算的结果，即所求的答案。
得到的数字通过sprintf函数转换为CString格式显示到屏幕上。同时，程序会进行初始化状态，并将结果储存到专门用于储存历史记录的数组当中。

calculate()//后缀式计算
{
while (postfix[i] != '\0')
 {
  if (postfix[i] >= '0'&&postfix[i] <= '9' || postfix[i] == '.')//如果是数字或者是小数点
  {
   num = spellnum(postfix, i);//转换为数字
   opnd.push(num);//放入数字栈中
  }
  else if (postfix[i] == ' ') i++;//空格代表各个组成部分分开
  else if (postfix[i]=='m'|| postfix[i] == '+'|| postfix[i] == '-'|| postfix[i] == '*'|| postfix[i] == '/'||postfix[i]=='^')
  {
   b = opnd.top();
   opnd.pop();
   a = opnd.top();
   opnd.pop();
   if (postfix[i] == 'm')//如果是取余
      int(a) % int(b)；
   if (postfix[i] == '+') num = a + b;
   if (postfix[i] == '-') num = a - b;
   if (postfix[i] == '*') num = a * b;
   if (postfix[i] == '/') num = a / b;//此处省略除数为0的操作
   opnd.push(num);//将算出的数字推入栈中
   i++;
   }//接最上面while循环的括号
   num = opnd.top();//取最上面的数字，既是最终答案
 opnd.pop();
 return num;

spellnum(char *fix, int &i)//计算数字
{
 int power=1;
 double num1 = 0, num2 = 0;
 while (fix[i] >= '0'&&fix[i] <= '9')//整数部分
  num1 = num1 * 10 + fix[i++] - '0';
 if (fix[i] == '.')//小数部分
 {
  i++;
  while (fix[i] >= '0'&&fix[i] <= '9')
   num2 += (double)(fix[i++] - '0')/ pow(10, power++);
 }
 return num1 + num2;

这些就基本组成了普通计算器的全部内容，需要注意的是，上述过程除了用户输入中缀式之外，都是在用户按下等号键之后进行的操作。当然这只是最基础的制作还有一些进阶的操作会更加的复杂，有兴趣的可以等候我的下一篇博客来讲述一些更复杂的操作，谢谢大家的收看。最后附上我制作的计算器的图片：

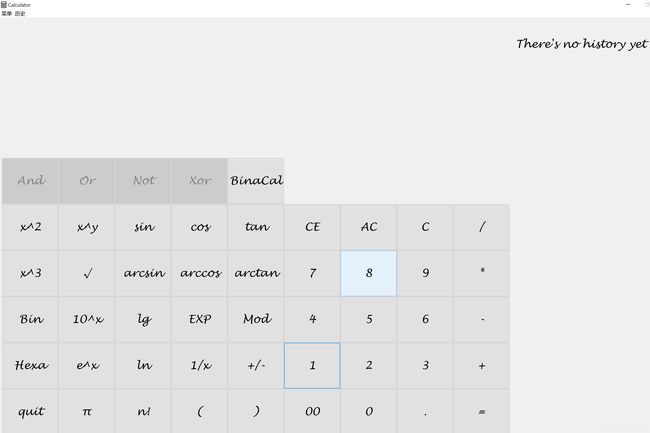
（除了基础的计算器功能之外，还增加了二进制和十六进制与十进制的转换以及专属的二进制运算）

参考文献：算法与数据结构（c++语言版）中国工信出版社 电子工业出版社