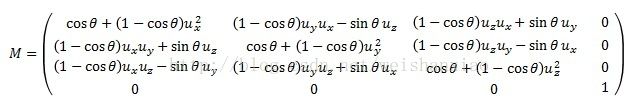零基础开发OpenGL ES 2.0学习笔记－变换矩阵

基本变换的相关数学知识

基本变换都是通过将表示点坐标的向量与特定的变换矩阵相乘完成的，进行基于矩阵的变换时，三维空间中点的位置需要表示成齐次坐标形式。

所谓齐次坐标形式也就是在x,y,z 3个坐标值后面增加第四个量w，未变换时w值一般为1，如P=(Px, Py, Pz, 1)T。

*（关于齐次坐标的概念，详见上一节）

P与一个特定的变换矩阵M相乘即可完成一次基本变换，得到变换后的点Q的齐次坐标向量，如Q(Qx, Qy, Qz, 1)T，具体情况如下所列。

┌  ┐   ┌               ┐   ┌  ┐
│Qx│   │m11 m12 m13 m14│   │Px│
│Qy│ = │m21 m22 m23 m24│ × │Py│ 或简写为：Q=MP
│Qz│   │m31 m32 m33 m34│   │Pz│
│ 1│   │ 0   0   0   1 │   │ 1│
└  ┘   └               ┘   └  ┘

---

说明：上述线性代数表达式是最左侧为变换后Q点的齐次坐标，中间的为4x4的变换矩阵，右侧为变换前P点的齐次坐标。

---

当矩阵M中的元素取适当的值时，等式Q=MP就会有其特殊的几何意义。例如，可以将三维空间中的点P平移，旋转或缩放到点Q。这些变换的具体信息就存放在矩阵M中，因此通常称矩阵M为变换矩阵。当需要连续执行一系列的变换时，依次将变换矩阵乘以表示点位置的齐次坐标向量即可。

 

平移矩阵

平移矩阵的基本格式如下：

    ┌        ┐
    │1 0 0 mx│
M = │0 1 0 my│
    │0 0 1 mz│
    │0 0 0  1│
    └        ┘

上述矩阵的mx,my,mz分别表示平移交换中沿x,y,z轴方向的位移。通过简单的线性代数计算即可验证，矩阵M乘以变换前P点的齐次坐标后确实得到了相当于将P点沿x,y,z轴平移mx,my,mz的结果，具体情况如下。

     ┌        ┐┌  ┐   ┌     ┐  　┌  ┐   ┌     ┐
     │1 0 0 mx││Px│   │Px+mx│  　│Qx│   │Px+mx│
MP = │0 1 0 my││Py│ = │Py+my│, 即│Qy│ = │Py+my│
     │0 0 1 mz││Pz│   │Pz+mz│  　│Qz│   │Pz+mz│
     │0 0 0  1││ 1│   │  1  │  　│ 1│   │  1  │
     └        ┘└  ┘   └     ┘  　└  ┘   └     ┘

 

旋转矩阵

介绍旋转变换的矩阵之前，首先需要了解一下绕坐标轴或任意轴旋转的一些规定。OpenGL ES中，旋转角度的正负可以用右手螺旋定则确定。所谓右手螺旋定则是指：右手握住旋转轴。使大拇指指向旋转轴的正方向，4指环绕的方向即为旋转的正方向，也就是旋转角度为正值。

旋转矩阵的基本格式如下：

上述矩阵表示将指定的点P绕轴向量u旋转θ度，其中的ux,uy,uz表示u向量在x,y,z轴上的分量。

 

缩放矩阵

缩放矩阵的基本格式如下：

    ┌          ┐
    │Sx  0  0 0│
M = │ 0 Sy  0 0│
    │ 0  0 Sz 0│
    │ 0  0  0 1│
    └          ┘

上述矩阵中的Sx,Sy,Sz分别表示缩放变换中的沿x,y,z轴方向的缩放率。通过简单的线性代数计算即可验证，矩阵M乘以变换前P点的齐次坐标后确实得到了相当于将P点坐标沿x,y,z轴方向缩放Sx,Sy,Sz倍的结果，具体情况如下。

     ┌          ┐┌  ┐   ┌    ┐  　┌  ┐   ┌    ┐
     │Sx  0  0 0││Px│   │SxPx│  　│Qx│   │SxPx│
MP = │ 0 Sy  0 0││Py│ = │SyPy│, 即│Qy│ = │SyPy│
     │ 0  0 Sz 0││Pz│   │SzPz│  　│Qz│   │SzPz│
     │ 0  0  0 1││ 1│   │ 1  │  　│ 1│   │ 1  │
     └          ┘└  ┘   └    ┘  　└  ┘   └    ┘