树与图的DFS
树与图的DFS
先声明一下,请大家看完我们的DFS讲解
这是本期对应是视频~
DFS B站讲解~
然后我们来讲一下。
建议一遍看分享一遍看B站效果最佳~
首先啥是DFS?
DFS,全程深度优先搜索(深度优先遍历),就是一条路走到底。
比如我们举一个例子:

我们去深搜便利这个图。
深搜的顺序如红色线条。
接下来我们看一个有回溯的深搜便利。
啥是回溯这里在说一遍。
回溯就是只无路可走是像回倒退的这个搜索过程。
那我们看看需要回溯的图应该如何进行深搜:
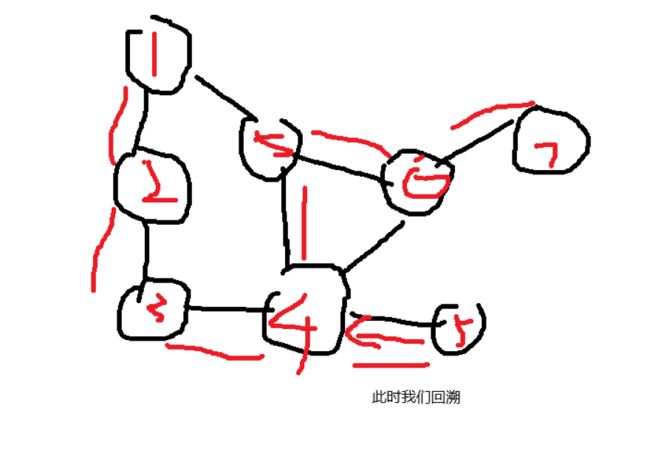
大家看我们中间回溯了一次因为我们已经走到了头。
当然有向图也是深搜的,这里因时间关系不多说了。
好接下来我们看一下深搜的模板:
int dfs(int u)
{
st[u] = true;//标记下
for(int i = h[u]; i != -1; i = ne[i])//链表便利方式,明天就会详解~
{
int j = e[i];//找到正在便利的点
if(!st[j])
{
int s = dfs(j);
//干一些事情
}
}
//干一些事情
}
是不是巨弱?
那我们具体应该如何存储一个图呢?
答案是:邻接表。
邻接表是单链表的一种,可以模拟(下节课我们讲链表,大家关注h)
然后这里简单说一下插入。
插入链表模板:
void add_to_lianbiao(int k, int x)
{
e[idx] = x, ne[idx] = ne[k], ne[k] = idx ++;
}
这里的idx表示当前我们用到了哪个点。
然后我们看下如何用邻接表去插入一个点。
void add_to_tu(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
最后我们开始做一道练习~
树的中心DFS练习。
本题让我们输出删掉某节点后最大连通块点数。
那具体咋搜呢?。
首先我们定义一下。
const int N = 100010, M = N * 2;//因为这里是无向图所以边=点*2
int n, h[N], e[M], ne[M], idx,ans = N;//功能你都清楚。h存的是图,剩下的是链表要用的,ans存最大值
bool st[N];//判断点是不是被搜过
然后add函数走起!(那个神经病在这里嚷嚷?)
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
读入读出。(我真能水)
int main()
{
cin >> n;
for(int i = 0; i < n - 1; i ++)
{
int a, b;
cin >> a >> b;
add(a, b),add(b, a);
}
dfs(1);
cout << ans << endl;
return 0;
}
dfs来了!
int dfs(int u)
{
st[u] = true;
int sum = 1, res = 0;
for(int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];//标准模板上线
if(!st[j])
{
int s = dfs(j);
res = max(res, s);
sum += s;
}
}
res = max(res, n - sum);
ans = min(ans, res);
return sum;
}
完整代码:
#include
using namespace std;
const int N = 100010, M = N * 2;
int h[N], ne[M], e[M], idx, ans = N, n;
bool st[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
int dfs(int u)
{
st[u] = true;
int sum = 1, res = 0;
for(int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if(!st[j])
{
int s = dfs(j);
res = max(res, s);
sum += s;
}
}
res = max(res, n - sum);
ans = min(ans, res);
return sum;
}
int main()
{
cin >> n;
memset(h, -1, sizeof h);
for(int i = 0; i < n - 1; i ++)
{
int a,b;
cin >> a >> b;
add(a, b), add(b, a);
}
dfs(1);
cout<< ans << endl;
return 0;
}