线性回归
这篇博客为大家简单介绍线性回归模型,也是写的第一篇回归模型的博客。
之前介绍的模型预测结果都是离散值,也就是机器学习当中的分类问题,那么机器学习中还有一大类预测问题,其预测结果为连续值,我们称之为回归问题。
线性回归属于机器学习中最基础的回归模型,因此,首先介绍线性回归模型。
虽然线性回归模型是最基础的模型,但是其重要性也是不容小觑的。在很多实际项目应用当中,其效果还是不错的。
首先我们用一个案例来引出线性回归:
假设我们要预测某个房子的价格,那么我们如何去预测得知房屋的价格呢?通常情况下我们会综合考虑各个因素之后再给出这个房子的估价。这些因素有可能是房屋面积,卧室数目,房屋所处楼层,是否为学区房等等。当我们掌握了这些信息之后我们便能够基本预测得知这个房子的大概的价格。然而这只是凭借我们的经验来进行预测得知的价格,实际上我们并不知道这些因素同房价之间的真正的关系。线性回归要解决的问题就是找到这些因素同房价之间的真实关系,在已知其关系的情况下,我们就能根据已知的这些因素去预测得到房屋的价格。上文中所说的因素也就是机器学习中的样本的特征。如下表所示:
| 房屋面积 |
卧室数目 |
所处楼层 |
是否学区房 |
房屋价格 |
| 123 | 3 | 2 | 1 | 1000000 |
| 90 | 2 | 6 | 0 | 600000 |
表中每一行为一个房屋的特征信息以及价格信息,我们称之为一个样本![]() ,其中
,其中![]() 代表房屋的各个特征。假设房屋价格
代表房屋的各个特征。假设房屋价格![]() 与各个特征之间的关系为
与各个特征之间的关系为![]() ,设
,设![]() ,
,![]() ,那么
,那么![]() ,这便是线性回归的基本模型,注意,线性回归并不是指关于特征是线性的,而是说关于权重向量
,这便是线性回归的基本模型,注意,线性回归并不是指关于特征是线性的,而是说关于权重向量![]() 是线性的,我们的任务就是要寻找最优的权重向量
是线性的,我们的任务就是要寻找最优的权重向量![]() ,从而确定特征
,从而确定特征![]() 和标记
和标记![]() 之间的关系。
之间的关系。
当![]() 确定后,则线性回归模型也就确定,
确定后,则线性回归模型也就确定,![]() ,其中
,其中![]() 为样本的预测值。
为样本的预测值。
接下来我们就来探索如何求得最好的![]() :
:
假设存在样本集![]() ,其中
,其中![]() 为第i个样本的特征向量,
为第i个样本的特征向量,![]() 为样本的真实标记。
为样本的真实标记。
现在我们已知存在一组初始的权重向量![]() ,构造出了一个初始线性模型
,构造出了一个初始线性模型![]() ,但是这个模型的预测效果并不是很好,因此我们需要对其进行优化。
,但是这个模型的预测效果并不是很好,因此我们需要对其进行优化。
在当前模型下,给定样本特征向量![]() ,我们可以得到其预测值
,我们可以得到其预测值![]() 。因此,我们也可以得到其预测误差
。因此,我们也可以得到其预测误差![]() 。
。
由于上式与![]() 时
时![]() 的概率密度一致,因此我们可以重新解释上式为
的概率密度一致,因此我们可以重新解释上式为![]() 。由此便可以的出似然函数
。由此便可以的出似然函数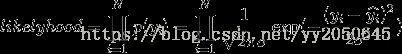 ,可以看出似然函数中的变量只有
,可以看出似然函数中的变量只有![]() ,我们只需要找出使得似然函数最大的权重向量
,我们只需要找出使得似然函数最大的权重向量![]() 即可,即
即可,即![]() 。
。
由于似然函数中![]() 为常数,所以我们将其省略,之后再对其取对数求取对数似然函数得到
为常数,所以我们将其省略,之后再对其取对数求取对数似然函数得到 ,省略
,省略![]() 可以得到
可以得到 。我们只需使得对数似然函数最大即可,因此
。我们只需使得对数似然函数最大即可,因此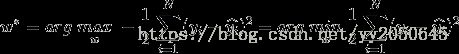 。
。
由此我们便退出了线性回归的损失函数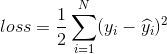 ,因此
,因此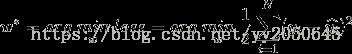 ,最后只需要对损失函数进行优化即可。
,最后只需要对损失函数进行优化即可。
在这里我们依旧采用梯度下降法:
接下来附上本人使用python编写的linear regression的程序:
import numpy as np
from numpy import random as rd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
rd.seed(2)
np.set_printoptions(linewidth=1000, suppress=True)
def generate_samples(count):
"""
:param count: 样本的个数
:return:
"""
x = rd.uniform(-10, 10, count)
y = 3.5 * x + 4 + rd.uniform(-5, 5, count)
x_return = np.ones((count, 1))
x_return = np.concatenate([x_return, x.reshape(-1, 1)], axis=1)
return x_return, y
class LinearRegression(object):
def __init__(self, count, alpha, lamda, beta, iter_times):
"""
:param lamda: 正则项系数
:param count: 生成样本个数,样本容量
:param alpha: 学习率
:param beta: 学习率衰减系数
:param iter_times: 多少个epoch
"""
self.iter_times = iter_times
self.beta = beta
self.lamda = lamda
self.alpha = alpha
self.x, self.y = generate_samples(count)
self.x_train, self.x_test, self.y_train, self.y_test = train_test_split(self.x, self.y, test_size=0.3, random_state=1)
self.weight = rd.uniform(-10, 10, 2)
self.batch_size = int(0.2 * self.x_train.shape[0])
self.epoch = int(np.ceil(self.x_train.shape[0] / self.batch_size))
# self.test_mses以及self.train_mses用于存放每一个epoch训练集和测试集的均方误差
self.test_mses = []
self.train_mses = []
def train(self):
for j in range(self.iter_times):
# 第一层循环控制多少个epoch
for i in range(self.epoch):
# 第二层循环完成一次就是一个epoch,每次遍历出一个batch
if i != (self.epoch - 1):
self.x_epoch = self.x_train[i * self.batch_size:(i + 1) * self.batch_size, :]
self.y_epoch = self.y_train[i * self.batch_size:(i + 1) * self.batch_size]
else:
self.x_epoch = self.x_train[i * self.batch_size:, :]
self.y_epoch = self.y_train[i * self.batch_size:]
self.weight -= self.alpha * (-np.sum((self.y_epoch.reshape(-1, 1) - np.dot(self.x_epoch, self.weight.reshape(-1, 1))) * self.x_epoch, axis=0) + 2 * self.lamda * self.weight)
# print(self.weight)
self.alpha *= self.beta
try:
mse_train = mean_squared_error(self.y_train, np.dot(self.x_train, self.weight.reshape(-1, 1)).ravel())
mse_test = mean_squared_error(self.y_test, np.dot(self.x_test, self.weight.reshape(-1, 1)).ravel())
self.train_mses.append(mse_train)
self.test_mses.append(mse_test)
except ValueError as e:
raise Exception("学习率设置过大")
if (j + 1) % int(0.1 * self.iter_times) == 0:
print("================epoch: %d================" % (j + 1))
print("第%d个epoch训练集均方误差:" % (j + 1), mse_train)
print("第%d个epoch测试集均方误差:" % (j + 1), mse_test)
def draw_mses(self):
fig = plt.figure()
ax = plt.subplot(2, 1, 1)
ax2 = plt.subplot(2, 1, 2)
plt.sca(ax)
ax.plot(np.arange(1, 1 + self.iter_times), self.train_mses, label="train dataset mse", color="g")
ax.plot(np.arange(1, 1 + self.iter_times), self.test_mses, label="test dataset mse", color="y")
ax.set_xlabel("epoch")
ax.set_ylabel("mse")
ax.set_title("mse")
ax.legend(loc="upper right")
plt.sca(ax2)
ax2.scatter(self.x[:, 1], self.y, label="samples", marker="*", color="r")
x = np.linspace(-10, 10, 1000).reshape(-1, 1)
x = np.concatenate([np.ones((1000, 1)), x], axis=1)
ax2.plot(x[:, 1].ravel(), np.dot(x, self.weight.reshape(-1, 1)).ravel(), color="b", label="fitness curve")
ax2.set_xlabel("x")
ax2.set_ylabel("y")
ax2.set_title("fitness curve")
ax2.legend(loc="upper left")
plt.subplots_adjust(wspace=10, hspace=0.5)
plt.show()
def main():
linear = LinearRegression(100, 0.001, 0.8, 0.99, 200)
linear.train()
linear.draw_mses()
if __name__ == "__main__":
main()
