剑指offer刷题详细分析：part11：51题——55题

• 剑指offer所有题目详解，可访问我的github项目：KongJetLin-offer

• 目录

1. Number51：构建乘积数组
2. Number52：正则表达式匹配
3. Number53：表示数值的字符串
4. Number54：字符流中第一个不重复的数字
5. Number55：链表中环的入口结点

---

题目51 构建乘积数组

  题目描述：给定一个数组A[0,1,…,n-1],请构建一个数组B[0,1,…,n-1],其中B中的元素B[i]=A[0] * A[1] *… * A[i-1] * A[i+1] *… * A[n-1]。不能使用除法。（注意：规定B[0] = A[1] * A[2] * … * A[n-1]，B[n-1] = A[0] * A[1] * … * A[n-2];）

  分析：我们可以使用 2个数组实现，一个数组存储 i 左边 A[0] - A[i-1]的乘积，另一个数组存储 i 右边 A[i+1] - A[length-1] 的乘积。有另一个更加好的方法，只使用一个数组，先存储 A[0] - A[i-1]的乘积，再将对应的数 乘以 A[i+1] - A[length-1] 的乘积，便可得到结果！

  代码如下：

public static int[] multiply(int[] A)
    {
     
        if(A == null || A.length<2)
            return null;//要构成乘积数组，A最少得有2个元素

        int[] res = new int[A.length];//乘积数组的长度与A数组长度相同

        //定义一个变量存储 i 左边数的乘积。对于 res[i]，left = res[0]*res[1]*...*res[i-1]
        // 对于乘积数组第一个元素 res[0] = res[1]*res[2]*...*res[A.length-1]，无左边乘积，因此left初始值设置为1
        int left = 1;
        for (int i = 0; i < A.length ; i++)
        {
     
            res[i] = left;// left = 1*res[0]*res[1]*...*res[i-1]
            //当 i=A.length-1，left不需要在乘以 A[A.length-1]，因为此时left若乘以A[A.length-1]，left没有对应的乘积数组的数
            if(i != A.length-1)//不判断其实也没有关系
                left *= A[i];//更新left
        }

        // 同样，义一个变量存储右边数的乘积。对于 res[i]，right = res[i+1]*res[i+2]*...*res[A.length-1]
        // 对于乘积数组最后一个元素 res[A.length-1] = res[0]*res[2]*...*res[A.length-2]，无右边乘积，因此right初始值设置为1
        int right = 1;
        for (int i = A.length-1; i >= 0 ; i--)
        {
     
            res[i] *= right;//将 res[i] 左边的乘积乘以右边的乘积
            if(i != 0)//不判断其实也没有关系
                right *= A[i];//更新right
        }

        return res;
    }

---

题目52 正则表达式匹配

  题目描述：请实现一个函数用来匹配包括’.‘和’‘的正则表达式。模式中的字符’.‘表示任意一个字符，而’'表示它前面的字符可以出现任意次（包含0次）。 在本题中，匹配是指字符串的所有字符匹配整个模式。例如，字符串"aaa"与模式"a.a"和"abaca"匹配，但是与"aa.a"和"ab*a"均不匹配。

  这个题需要考虑的情况比较多，需要谨慎考虑。我们将2个串分别命名为匹配串和模式串。
  首先，我们匹配第一个字符，对于模式串，第一个字符不可能是“ * ”。
1、当模式串的第二个字符不是“ * ”的时候：如果模式串的第一个字符是“.”，或者模式串的第一个字符与匹配串的第一个字符相同，匹配成功，那么我们将模式串与匹配串都向后移动一位，匹配下一个字符；如果模式串与匹配串匹配失败，直接返回false。
2、当模式串的第二个字符是“ * ”的时候：由于“ * ”表示它前面一个字符可以出现0次或者1到多次，此时会影响第一个字符的匹配，我们还需要分情况：
  1）如果模式串第一个字符与匹配串第一个字符不匹配，模式串的“ * ”表示模式串前一个字符出现0次，将模式串字符后移2位，那么我们继续用匹配串的第一个字符与此事的模式串比较。
  2）如果模式串第一个字符与匹配串第一个字符相匹配，此时还可以分为3种情况：
     i）即使第一个字符匹配，我们也可以将其视为不匹配，因为 “星号”（为了使得页面不混乱，这里将出现一次或者多次的符号叫做星号）本来就可以表示匹配0次，我们将模式串后移2位。匹配串不移动，继续与模式串进行匹配；
     ii）“星号”表示匹配一次，那么我们将模式串与匹配串都向后移动1位即可；
     iii）“星号”表示匹配多次，我们将匹配串后移一位，模式串不变。
  代码如下：

public boolean match(char[] str, char[] pattern)
    {
     
        if(str==null || pattern==null)
            return false;
        //我们从2个数组的0位置开始匹配
        return match(str , 0 , pattern ,0);
    }

    private boolean match(char[] str, int indexStr , char[] pattern , int indexPat)
    {
     
        //当indexStr=str.length与indexPat=pattern.length，说明2个数组同时到达末尾，匹配成功
        if(indexStr==str.length && indexPat==pattern.length)
            return true;
        //当匹配字符串str还没有匹配完，但是模式字符串结束了，一定匹配失败
        if(indexStr<str.length && indexPat==pattern.length)
            return false;
        /**
        当匹配字符串匹配完，但是模式字符串还没有匹配完，此时可能匹配成功，也看匹配失败。
         如果模式字符串后面是“*”或者“字符*”，“*”可以表示匹配0个，那么就会成功；
         如果模式字符串后面是其他字符串，就会失败。
         我们这里不需要进行判断，直接进行下面的判断，下面就会根据模式字符串是不是“*”或者“字符*”进行判断，从而返回相应的结果。
         */

        /**
        注意，下面不需要再判断 indexPat

        //如果模式字符串下一个字符存在且为“*”，那么当前模式字符串为 "indexPat*"
        if(indexPat+1<pattern.length && pattern[indexPat+1] == '*')
        {
     
            /**
             如果当前的匹配字符串与模式字符串项匹配，有可以分为3种情况
             “*”表示匹配0个，1个或者多个，只要这几个其中有一个满足即可！
             */
            if((indexStr<str.length && str[indexStr]==pattern[indexPat]) || (indexStr<str.length && pattern[indexPat]=='.'))
            {
     
                //下面这片注释和代码我理解错误
//                boolean zero = match(str , indexStr , pattern , indexPat+2);//匹配0个的结果
//                boolean one = match(str , indexStr+1 , pattern , indexPat+2);//匹配1个的结果
                /**
                如果“*”要表示匹配多个，那么匹配串的这一个indexStr的字符必须与indexStr+1的字符相同，否则可能出错。如下：

                 比如我们匹配 “ab”(匹配串str)与“.*”(模式串pattern).我们知道最终结果是匹配失败。
                 第一次比较：indexPat(0)+1=1<2，此时“a”与“.”相匹配，如果选择模式串的“*”匹配多个，此时 indexStr+1=1，而indexPat=0不变继续匹配。
                 第二层比较：indexPat(0)+1=1<2，此时“b”与“.”相匹配，如果选择模式串的“*”匹配一个，indexStr+1=2，indexPat+2=2，结束
                 那么最后就会返回true，与实际结果相悖。
                 */
//                boolean many = false;
//                //当然，模式串的“*”匹配多个匹配串字符，前提是匹配串的下一个字符存在
//                if(indexStr+1
//                {
     
//                    many = match(str , indexStr+1 , pattern , indexPat);
//                }
//
//                return zero || one || many;

                /**
                此处牛客网测试用例："ab",".*" 返回true，即“.*”不是表示任意字符出现一次或者多次，如“aaaa”；而是表示出现0个或者多个任意字符，如“abc”。（上面代码我理解错误！）
                 如果是“ab”,"a*"，那么"*"无法表示匹配多个“a”，因为匹配串第二个字符是“b”
                 
                 那么上面的代码就可以简化。
                 即这里模式串“*”匹配多次的时候，匹配串的这一个indexStr的字符不一定需要与indexStr+1的字符相同。
                 */
                return match(str , indexStr , pattern , indexPat+2)//0个
                        || match(str , indexStr+1 , pattern , indexPat+2)//1个
                        || match(str , indexStr+1 , pattern , indexPat);//多个
            }
            else
            {
     
                /**
                 如果当前的匹配字符串与模式字符串项不匹配，那么此时 模式字符串"indexPat*"的“*”只能表示为 indexPat 出现0次。
                 那么将模式字符串后移2位，匹配字符串不动，继续递归比较，注意返回递归的结果
                 */
                return match(str , indexStr , pattern , indexPat+2);
            }

        }
        else
        {
     
            /**
            如果模式字符串下一个字符存在且不为“*”，或者模式字符串的下一个字符不存在，
             那么此时下一个字符串肯定不是“*”，对当前模式字符的判断不会造成影响，
             那么我们可以直接判断当前匹配字符与模式字符。（此时当前匹配字符必然存在，只需要判断当前模式字符是否存在即可）
             */
            //我们可以直接判断这一个匹配字符串与模式字符串是否匹配
            if((indexStr<str.length && str[indexStr]==pattern[indexPat]) || (indexStr<str.length && pattern[indexPat]=='.'))
            {
     
                //当前的匹配字符串与模式字符串项匹配，则递归匹配他们的下一个字符串，注意返回递归的结果
                return match(str , indexStr+1 , pattern , indexPat+1);
            }
            else
                return false;//匹配失败直接返回false
        }
    }

---

题目53 表示数值的字符串

  题目描述：请实现一个函数用来判断字符串是否表示数值（包括整数和小数）。例如，字符串"+100",“5e2”,"-123",“3.1416"和”-1E-16"都表示数值。 但是"12e",“1a3.14”,“1.2.3”,"±5"和"12e+4.3"都不是。

  使用正则表达式的方式匹配。表示数值的字符串的形式可以表示为：

A[.[B]][(e/E)C] 或者是 .B[(e/E)C]

  A为数值的整数部分，B为跟在小数点之后的小数部分，（e/E）为指数标志，C为跟在e或者E之后的指数部分。
  其中，A部分可以没有，比如小数.123代表0.123。如果一个数没有整数部分，那么小数部分必须有。对于小数部分，如果小数点存在，其后必须带有数字。对于指数部分，如果有e/E存在，其后必须带有数字。A和C（也就是整数部分和指数部分）都是可能以"+"、"-"开头或者没有符号的数字串，B是数字序列，但前面不能有符号。
  具体的正则表达式如下：

“[+-]?\\d*(\\.\\d+)?([eE][+-]?\\d+)?”

其中，
[+-]? ：表示“+”或者“-”出现一次或者0次；
\\d* ：表示整数部分出现0次或者多次；
(\\.\\d+)? ： 分组表示“.”和小数必须一同出现，且出现0次或者多次。其中，\\d+ 为小数部分，必须出现至少一次。
([eE][+-]?\\d+)? ： 指数部分，分组表示指数部分必须一起出现。[+-]? 表示“+”或者“-”出现一次或者多次。\\d+ 表示指数部分的数字出现一次或者多次，即有“e/E”，则其后必须有数字。

  代码如下：

public boolean isNumeric(char[] str)
    {
     
        if(str==null || str.length==0)
            return false;

        return new String(str).matches("[+-]?\\d*(\\.\\d+)?([eE][+-]?\\d+)?");
        /**
         为什么是两个反斜杠？我们以“\\.”的转义过程来说明
         第一步，编译器将字符串转变为“正则表达式”
            此时，将字符中的“\\”解析为“\”，整体被解析为正则表达式“\.”
         第二步，才开始把第一步的结果当做是正则表达式，开始进行匹配！
		    作为正则表达式，“\.”又被正则表达式引擎解释为“.”
		如果在字符串里只写\.的话，第一步就被直接解释为.，之后作为正则表达式被解释时就变成匹配任意字符了
         */
    }

---

题目54 字符流中第一个不重复的数字

  题目描述：请实现一个函数用来找出字符流中第一个只出现一次的字符。例如，当从字符流中只读出前两个字符"go"时，第一个只出现一次的字符是"g"。当从该字符流中读出前六个字符“google"时，第一个只出现一次的字符是"l"。
  输出描述:如果当前字符流没有存在出现一次的字符，返回#字符。

方法1：使用HashMap实现
  分析：最直观的解法是使用 HashMap 对出现次数进行统计，键为字符，值为字符出现的次数。当然还需要一个 StringBuilder 来记录字符流中字符出现的顺序。
  这种方法需要一个 HashMap 与 StringBuilder ，空间复杂度是 O(2n)；且 StringBuilder 在插入元素的时候，每次插入的时间复杂度都是 O(n)，最后 FirstAppearingOnce () 方法也需要一个时间复杂度为 O(n) 的遍历。

//定义一个HashMap
    HashMap<Character , Integer> hashMap = new HashMap();
    /*
    这里我们还需要一个 StringBuilder，因为我们将元素存储到HashMap的key，
    HashMap是会根据key的hashCode再进行hash计算，然后按照hash值放入集合，并不是按照元素在字符流中出现的先后放入HashMap，
    即 HashMap 中 key 的顺序与字符流中key的顺序不同，因此，我们需一个 StringBuilder 来记录字符流中元素出现的顺序。
     */
    StringBuilder sb = new StringBuilder();

    //Insert one char from stringstream（从字符流取出一个字符插入我们的HashMap）
    public void Insert(char ch)
    {
     
        sb.append(ch);//取出一个元素就向 StringBuilder 插入一个元素
        if(!hashMap.containsKey(ch))
        {
     
            hashMap.put(ch , 1);
        }
        else
        {
     
            hashMap.put(ch , hashMap.get(ch)+1);
        }

    }
    //return the first appearence once char in current stringstream
    public char FirstAppearingOnce()
    {
     
        for (int i = 0; i < sb.length() ; i++)
        {
     
            if(hashMap.get(sb.charAt(i)) == 1)
                return sb.charAt(i);
        }
        return '#';
    }

方法2：使用二维数组实现
  这种方法只需要一个二维数组，空间复杂度是 O(n)；inerst() 方法只需修改二维数组 0,1 位置，时间复杂度是 O(1)；最后 FirstAppearingOnce () 方法也需要一个时间复杂度为 O(n) 的遍历。
  这种方法的技巧是，使用 字符 作为数组的下标！！！
   这题对比 剑指offer 34题： 第一个只出现一次的字符位置 的解法。

/*
    我们使用 ch 作为二维数组的第一个下标，二维数组第二个下标只有2个：0,1。
    0位置存储字符出现次数，1位置存储该字符第一次在字符流中出现的位置。

    其实如果测试的字符出现的次数小于 2^7，我们使用 byte[][] charArr = new byte[128][2]; 即可，byte 位置可以存储的数字最大为2^7。（测试通过）
     */
    int[][] charArr = new int[128][2];
    int time = 0;//用于记录字符在字符流中出现的位置

    //Insert one char from stringstream
    public void Insert(char ch)
    {
     
        if(charArr[ch][0] == 0)//字符第一次出现
        {
     
            charArr[ch][0] = 1;
            charArr[ch][1] = time++;//记录ch第一次在字符流出现的位置
        }
        else
        {
     
            charArr[ch][0] = -1;//如果出现多次，将其值设置为-1。不需要改变该字符第一次出现的位置
        }

    }
    //return the first appearence once char in current stringstream
    public char FirstAppearingOnce()
    {
     
        /*
        为什么将 first 设置为 Integer 最大值？
        first用于记录满足出现一次的字符在字符流中第一次出现的位置。可能有多个满足的字符。
        如果后面遍历到的字符出现位置比前面的first前，即
        int first = Integer.MAX_VALUE;
        char retCh = 0;
        for (int i = 0; i < charArr.length ; i++)
        {
     
            //如果当前字符满足出现一次，且第一次出现的位置小于前面满足的字符第一次出现的位置
            if(charArr[i][0] == 1 && charArr[i][1] < first)
            {
     
                retCh = (char)i;
                first = charArr[i][1];//更新first
            }
        }

        if(retCh == 0)
            return '#';
        return retCh;
    }

方法3：使用一维数组实现
  思路与第二种方法相似，不过这里使用一个队列来保存元素的顺序。这样 insert() 方法必定有一个 add() 和 remove() 方法，使用链表实现的队列，必然有一个是 O(n) 复杂度，insert() 方法的时间复杂度是 O(n)。但是对于 FirstAppearingOnce() 方法，只需要出队队首元素即可，时间复杂度是 O(1)。总体上空间复杂度是 O(2n)。

int[] arr = new int[256];
    Queue<Character> queue = new LinkedList<Character>();

    //Insert one char from stringstream
    public void Insert(char ch)
    {
     
        //先将元素添加到队列
        queue.add(ch);
        //数组相应 ‘ch’ 位置+1，表示该元素在字符流出现次数+1
        arr[ch]++;
        /*
        当队列不为null的时候，将队列中出现次数大于1的元素出队。
        这里不需要判断元素出现次数为0的情况，因为能在队列中出现的元素次数可能大于等于1.
        移除队列前面不满足的元素，剩下的就是满足的元素，只需要将第一个满足的元素出队即可！
        当然，这部分判断也可以在 FirstAppearingOnce() 方法中判断。
         */
        while (!queue.isEmpty() && arr[queue.peek()]>1)
            queue.remove();
    }
    //return the first appearence once char in current stringstream
    public char FirstAppearingOnce()
    {
     
        return queue.isEmpty() ? '#' : queue.peek();
    }

---

题目55 链表中环的入口结点

  题目描述：给一个链表，若其中包含环，请找出该链表的环的入口结点，否则，输出null。

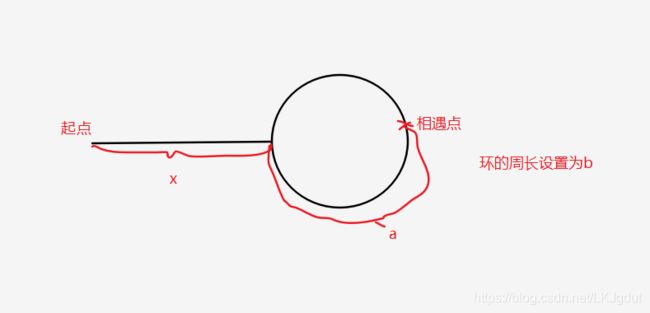
  分析：这题可以变换为一个追及问题，在追及问题中，我们可以用两个速度不同的物体从同一地点出发，如果路径中存在如下图的环，那么速度较快的物体最后一定会在环中的某一个点追到速度较慢的物体。如下图设起点到环入口点的距离为x，入口到相遇点的距离为a，然后物体逆时针前进。
  我们设置物体A与物体B同时从起点出发，设物体 A 速度是 v(a)，物体 B 速度是 v(b)，且物体A的速度是物体B速度的2倍，即 v(a) = 2v(b)。
  那么到相遇点，物体 A 走过的距离是 ：D(a) = x+a+mb（m是物体A走过的环数），物体 B 走过的距离是：D(b) = x+a+nb（n是物体B走过的环数）。由于A速度是B速度的2倍，那么有：D(a) = 2D(b)，即 2(x+a+nb) = x+a+mb，有：x = (m - 2n)b - a = (m -2n -1)b + (b - a)。
  什么是b - a？这是相遇点后，环后面部分的路程。此时 (m -2n -1) >=0，若 (m -2n -1)<0，由于 m,n 都是整数，那么 (m -2n -1)<=-1，那么 x= (m -2n -1)b + (b - a) <=-a < 0，不合法。即证 (m -2n -1) >=0 。
  那么，当物体A 与 物体B 相遇后，我们让物体A（速度较快）从新从结点出发，以速度 v(b) 走过 x = (m -2n -1)b + (b - a) 的距离，同时物体 B在相遇点出发，以速度 v(b) 走过 (m -2n -1)b + (b - a)。当物体 B 走过 (m -2n -1) 圈环，又走了 (b-a)的距离之后，刚刚好到达环的入口，而此时物体A同样走过 (m -2n -1)b + (b - a) 的距离，同样到达环的入口点，即此时他们会在环的入口点相遇。

  总结：使用双指针，一个指针 fast 每次移动两个节点，一个指针 slow 每次移动一个节点。因为存在环，所以两个指针必定相遇在环中的某个节点上。在相遇点，让 fast 重新从头开始移动，并且速度变为每次移动一个节点，而slow继续移动，速度仍然为每次移动一个结点，那么他们会在环的入口点相遇！

  代码如下：时间复杂度 O(n)，空间复杂度 O(1)

public ListNode EntryNodeOfLoop(ListNode pHead)
    {
     
        //首先，判断pHead是否合法
        if(pHead == null || pHead.next == null)
            return null;

        ListNode fast = pHead;
        ListNode slow = pHead;

        /**
         注意！！不能写作如下这种形式，因为fast与slow一开始就是相同的，这会让循环无法进行。
         我们应该使用 do..while()，使得fast与slow先移动一位变得不同，这样才能进入循环。

        while(fast != slow)
        {
            fast = fast.next.next;
            slow = slow.next;
        }
         */
        do {
     
            fast = fast.next.next;//2倍速
            slow = slow.next;//一倍速
        }while (fast != slow  || fast.next == null);

        //出循环 fast 与 slow相遇
        fast = pHead;//fast从新回到起点
        while (slow != fast)
        {
     
            fast = fast.next;
            slow = slow.next;
        }
        //出循环的时候，fast与slow在环的入口结点相遇
        return slow;
    }

  如果没有空间的要求，我们也可以使用 HashSet来实现。空间复杂度是 O(n)

public ListNode EntryNodeOfLoop1(ListNode pHead)
    {
     
        HashSet<ListNode> hs = new HashSet<>();
        while (pHead != null)
        {
     
            if(hs.contains(pHead))
                return pHead;
            hs.add(pHead);
            pHead = pHead.next;
        }
        return null;//不存在相同，没有环
    }