2019 ICPC上海站 网络赛 部分题解
L. Digit sum
打表。
#include
#define mem(a,b) memset((a),b,sizeof(a))
#define de cout<0)
{
ret+=(n%b);
n/=b;
}
return ret;
}
int main()
{
for(int i=1;i<=1000000;i++)
for(int j=2;j<=10;j++)
a[i][j]=0;
for(int i=1;i<=1000000;i++)
for(int j=2;j<=10;j++)
a[i][j]=a[i-1][j]+solve(i,j);
int T;scanf("%d",&T);
int TT=0;
while(T--)
{
int n,b;
scanf("%d%d",&n,&b);
printf("Case #%d: %lld\n",++TT,a[n][b]);
}
return 0;
} B. Light bulbs
思维题,不过不太好想。
#include
#define mem(a,b) memset((a),b,sizeof(a))
#define de cout< J. Stone game
倒着完全背包。
#include
#define mem(a,b) memset((a),b,sizeof(a))
#define de cout<=1;i--)
p[i]=p[i+1]+a[i];
ll p1=(sum+1)/2,p2;
for(int i=n;i>=1;i--)
{
p2=(sum+a[i])/2;
for(int j=p1;j<=p2;j++)
{
if(j=1;j--)
{
if(j-a[i]>=0)
dp[j]=(dp[j]+dp[j-a[i]])%mod;
else
break;
}
}
printf("%lld\n",ans);
}
return 0;
} D. Counting Sequences I
参考博客:https://blog.csdn.net/yzsjwd/article/details/100867148
暴力打表。
打表代码:
#include
#define mem(a,b) memset((a),b,sizeof(a))
#define de cout<0)
{
if(b&1)
ret=(ret*a)%mod;
a=(a*a)%mod;
b>>=1;
}
return ret;
}
void init()
{
f[0]=1;
f[1]=1;
for(int i=2; i<=3000; i++)
f[i]=f[i-1]*i%mod;
for(int i=1; i<=3000; i++)
invf[i]=pow_mod(f[i],mod-2);
}
/*
d:当前序列中非1的数的个数
p:序列中元素的最大值
n:非1元素最多有多少个
sum:当前和
prod:当前积
*/
void dfs(ll d,ll p,ll n,ll sum,ll prod)
{
ll t;
if(d==n) //非1的数的个数已经达到了
{
if(N>13)
t=N-13;
else
t=0;
if(sum+t==prod) //如果和等于积了
{
ll x=f[N];
x=(x*invf[cnt[1]+t])%mod;
for(int i=2;i<=6000;i++)
x=(x*invf[cnt[i]])%mod;
ans=(ans+x)%mod;
}
return ;
}
if(prod>6000)
return ;
for(int i=p;i<=6000/prod;i++)
{
cnt[i]++;
dfs(d+1,i,n,sum+i,prod*i);
cnt[i]--;
}
}
int main()
{
freopen("output.txt","w",stdout);
init();
f[0]=1;
invf[0]=1;
mem(cnt,0);
cout<<1;
for(N=2; N<=3000; N++)
{
ans=0;
ll t=min(N,1ll*13);
dfs(0,1,t,0,1);
cout<<","< AC代码:
#include
#define mem(a,b) memset((a),b,sizeof(a))
#define de cout< F. Rhyme scheme
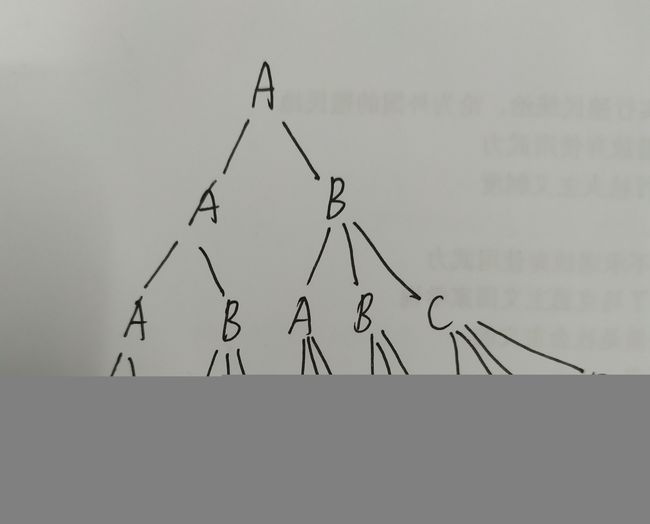
题意:求出合法的长度为n的字典序第k小字符串,合法的定义为除了最后一位,每一位的取值范围为'A'到'A'+pos-1,而最后一位的取值范围'A'到当前字符串最大值+1。
思路:dp求每个节点下面有多少种情况,如果此节点下的情况数大于等于k,那就输出这个节点,并且k-=这个节点下的情况数;否则,继续判断下一个节点。dp[n][i][j]表示输入的数为n时,第 i 层中某个节点下有多少种情况,并且这个节点需要满足的要求为这条线路上最大的字符为j(如果最大字符为‘A',那么j等1,如果最大字符为’Z',那么j等26)。
dp[i][j]=dp[i+1][j]*j+dp[i+1][j+1]。初始化dp[i][i][j]=1。i为1到26,j为1到i。详见代码。
因为当n等26的时候,dp会很大,long long存不下,所以要用到__int128,输出的话,必须用快读。听说用java会超时。
ACcode:20ms
#include
#define mem(a,b) memset((a),b,sizeof(a))
#define de cout<=1;j--)
{
for(int k=1;k<=j;k++)
dp[i][j][k]=dp[i][j+1][k]*k+dp[i][j+1][k+1];
}
}
}
inline __int128 read()
{
__int128 x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-')
f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=x*10+ch-'0';
ch=getchar();
}
return x*f;
}
//inline void print(__int128 x)
//{
// if(x<0)
// {
// putchar('-');
// x=-x;
// }
// if(x>9)
// print(x/10);
// putchar(x%10+'0');
//}
int main()
{
init();
int T;scanf("%d",&T);
int TT=0;
while(T--)
{
//scanf("%lld%lld",&n,&k);
//read(n);read(k);
n=read();k=read();
printf("Case #%d: ",++TT);
int p=1,mx;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=i;j++)
{
mx=max(p,j);
if(dp[n][i][mx]>=k)
{printf("%c",char(j+'A'-1));p=max(p,j);break;}
else
k-=dp[n][i][mx];
}
}
printf("\n");
}
return 0;
} C. Triple
题意:输入n,然后给你三个长度均为n的数组a、b、c,问你存在多少对i、j、k满足|Ai-Bj|<=C[k],且|Bj-Ck|<=Ai,且|Ai-Ck|<=Bj。
思路:FFT+容斥。
实际上题意可以转化一下,问的就是存在多少对ijk满足两边之和大于等于第三边,也就是满足“能构成三角形”或者“两边之和等于第三边”。那我们可以容斥一下,答案就是n*n*n-“有多少种情况满足任意两边之和小于第三边”。至于“有多少种情况满足任意两边之和小于第三边”我们可以FFT求。
还有,FFT的时间复杂度是O(n*longn)。当n小于等于1000的时候,可以直接O(n*n)暴力跑一下;如果n大于1000,再用FFT。至于为什么不能直接用FFT,好像是因为FFT的复杂度有一个很大的常数,当n小于等于1000的时候,O(n*n)是小于O(n*logn)+常数的。这个题还比较坑,就是如果你写成n小于等于1000直接O(n*n)就能过,但是如果写成n小于1000直接O(n*n)就会T......应该是因为有组n等1000的数据等着卡你。
ACcode:1986ms。
#include
#define mem(a,b) memset((a),b,sizeof(a))
#define de cout<>1]>>1)|((i&1)<<(L-1));
for (int i=0; i<=n; ++i)
a[i]=Complex(1.0*f[i],0.0),b[i]=Complex(1.0*g[i],0.0);
calc(1);
}
void init()
{
mem(f,0);
mem(g,0);
mem(F,0);
}
int main()
{
int T1;scanf("%d",&T1);
int TT=0;
while(T1--)
{
init();
scanf("%lld",&N);
for(int i=1;i<=N;i++)
scanf("%lld",&A[i]);
for(int i=1;i<=N;i++)
scanf("%lld",&B[i]);
for(int i=1;i<=N;i++)
//C[i]=read();
scanf("%lld",&C[i]);
sort(A+1,A+N+1);
sort(B+1,B+N+1);
sort(C+1,C+N+1);
mem(suma,0);
mem(sumb,0);
mem(sumc,0);
for(int i=1;i<=N;i++)
suma[A[i]]++;
for(int i=2;i<=A[N];i++)
suma[i]=suma[i-1]+suma[i];
for(int i=1;i<=N;i++)
sumb[B[i]]++;
for(int i=2;i<=B[N];i++)
sumb[i]=sumb[i-1]+sumb[i];
for(int i=1;i<=N;i++)
sumc[C[i]]++;
for(int i=2;i<=C[N];i++)
sumc[i]=sumc[i-1]+sumc[i];
ll ans=0;
if(N<=2000)
{
for(int i=1;i<=N;i++)
for(int j=1;j<=N;j++)
{
if(A[i]+B[j]>C[N])
break;
ans+=(N-sumc[A[i]+B[j]]);
}
for(int i=1;i<=N;i++)
for(int j=1;j<=N;j++)
{
if(A[i]+C[j]>B[N])
break;
ans+=(N-sumb[A[i]+C[j]]);
}
for(int i=1;i<=N;i++)
for(int j=1;j<=N;j++)
{
if(B[i]+C[j]>A[N])
break;
ans+=(N-suma[B[i]+C[j]]);
}
printf("Case #%d: ",++TT);
ans=N*N*N-ans;
printf("%lld\n",ans);
continue;
}
S=A[N] + 10;
T=B[N] + 10;
n=S+T+10;
for(int i=1;i<=N;i++)
f[A[i]]++;
for(int i=1;i<=N;i++)
g[B[i]]++;
solve();
for(int i=2;i<=n;i++)
{
if(i>C[N])
break;
ans+=(F[i]*(N-sumc[i]));
}
init();
S=A[N];
T=C[N];
n=S+T;
for(int i=1;i<=N;i++)
f[A[i]]++;
for(int i=1;i<=N;i++)
g[C[i]]++;
solve();
for(int i=2;i<=n;i++)
{
if(i>B[N])
break;
ans+=(F[i]*(N-sumb[i]));
}
init();
S=C[N];
T=B[N];
n=S+T;
for(int i=1;i<=N;i++)
f[C[i]]++;
for(int i=1;i<=N;i++)
g[B[i]]++;
solve();
for(int i=2;i<=n;i++)
{
if(i>A[N])
break;
ans+=(F[i]*(N-suma[i]));
}
printf("Case #%d: ",++TT);
ans=N*N*N-ans;
printf("%lld\n",ans);
}
return 0;
} E. Counting Sequences II
题意:让你构造一个长度为n的序列满足:1、序列中每个元素的值都在1到m之间;2、对于序列中任意一个偶数,需要满足它出现的次数是偶数。
思路:推公式,然后预处理,然后O(1)求组合数。
至于公式怎么退,我不会......
有篇感觉讲的很不错的博客,可我还是不会。https://www.cnblogs.com/heyuhhh/p/11545443.html
还有,这个题有个我不知道的地方就是,对于除法,除完后要取模,比如ans=a/b%mod,不能直接写成ans=a/b%mod,应该写成ans=a*pow_mod(b,mod-2,mod)%mod,也就是说要写成逆元的形式。
推公式的过程:
ACcode:148ms
#include
#define mem(a,b) memset((a),b,sizeof(a))
#define de cout<>=1;
a=a*a%mod;
}
return ret;
}
const int maxn = 2e5;
LL A[maxn];
LL B[maxn];
void Init()
{
A[0] = 1;
for(int i=1; i<=maxn; i++)
A[i] = (A[i-1] * i ) % mod;
}
LL Ext_Gcd(LL a, LL b, LL &x, LL &y)
{
if(b==0){
x=1;
y=0;
return a;
}
LL d = Ext_Gcd(b, a%b, y, x);
y-=a/b*x;
return d;
}
LL Inv(LL a, LL n)
{
LL x,y;
LL d = Ext_Gcd(a,n,x,y);
if(d == 1)
return ((x%n)+n)%n;
return -1;
}
LL get()
{
for(int i=0;i 其他的真不会了,以后再说吧......