数论之————中国剩余定理
中国剩余定理
在《孙子算经》中有这样一个问题:“今有物不知其数,三三数之剩二(除以3余2),五五数之剩三(除以5余3),七七数之剩二(除以7余2),问物几何?”这个问题称为“孙子问题”,该问题的一般解法国际上称为“中国剩余定理”。
首先,我们假设n1是满足除以3余2的一个数,也就是满足3∗k+2(k>=0)的一个任意数。同样,我们假设n2是满足除以5余3的一个数,n3是满足除以7余2的一个数。因为n1+n2+n3对3取余,余数还应该满足2,所以(n2+n3)%3==0,同理可得,(n1+n2)%7==0,(n1+n3)%5==0。
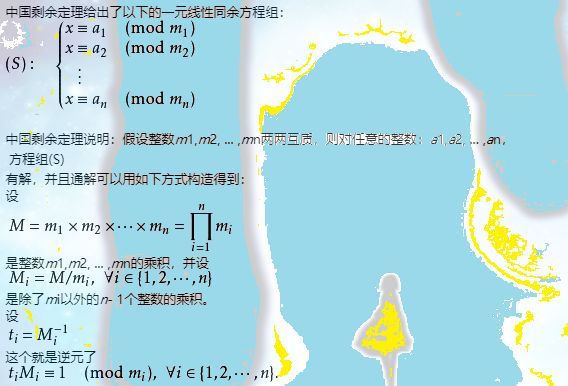
式子:ti*Mi=1 (mod mi)
可以写为: ti*Mi+mi*k=1
就可以用拓展欧几里得求解逆元Mi^-1。
不懂逆元的可以点这里~_~
就可以把
5*7*k%3==1
3*7*k%5==1
3*5*k%7==1
k=0,1,2….n
转化为乘逆元的形式,如下:
假设inv(x)为x的逆元
5*7*inv(5*7, 3) % 3 = 1
3*7*inv(3*7, 5) % 5 = 1
3*5*inv(3*5, 7) % 7 = 1
然后两边同乘余数
2 * 5*7*inv(5*7, 3) % 3 = 2
3 * 3*7*inv(3*7, 5) % 5 = 3
2 * 3*5*inv(3*5, 7) % 7 = 2
a=2 * 5*7*inv(5*7, 3) % 3
b=3 * 3*7*inv(3*7, 5) % 5
c=2 * 3*5*inv(3*5, 7) % 7
得到:
a%3=2;
b%5=3
c%7=2
答案就是a+b+c;
因为
a%5 = a%7 = 0 因为a是5的倍数,也是7的倍数
b%3 = b%7 = 0 因为b是3的倍数,也是7的倍数
c%3 = c%5 = 0 因为c是3的倍数,也是5的倍数
(a+b+c)%3=a%3+b%3+c%3=2+0+0
(a+b+c)%5=a%5+b%5+c%5=0+3+0
(a+b+c)%7=a%7+b%7+c%7=0+0+2
所以很明显了,答案就是a+b+c。
但这只是其中一个值,要求最小值,就用(a+b+c)%(3*5*7)。
代码模板:
int extgcd(int a,int b,int &x,int &y)
{
int d=a;
if(b!=0)
{
d=extgcd(b,a%b,y,x);
y-=(a/b)*x;
}
else
{
x=1; y=0;
}
return d;
}
int inv(int n,int m) //求逆元
{
int x,y;
int d=extgcd(n,m,x,y);
return d==1?(x%m+m)%m:-1;
}
int china()
{
int m=1,s=0;
for(int i=0;i<3;i++) m*=a[i]; //a[i]保存要除的数
for(int i=0;i<3;i++)
{
int w=m/a[i];
s=(s+w*inv(w,a[i])*b[i])%m; //b[i]保存余数
}
return (s+m)%m;
}——————————————————————————————————————————————————————
但是上边只符合m1,m2,m3….互素的情况。如果不互素就要使用线性同余方程组来求解。
ai*x≡bi (mod mi) (1<=i<=n) 如果方程组有解,一定有无穷多解,而且解得全集一定可以写成x ≡ b (mod m)的形式,问题就转为求b和m。求解方程组x ≡ b1 (mod m1) a*x ≡ b2 (mod m2)。
x ≡ b1 (mod m1) —–>x=b1+m1*t 带入第二个式子。
得到:a(b1+m1*t) ≡ b2 (mod m2)
移项后:a*m1*t ≡ b2-a*b1 (mod m2)
当gcd(m2,a*m1)%(b2-a*b1) ! = 0 原方程无解
模板代码:
pair linear(int A[],int B[],int M[])
{
LL x=0,m=1;
for(int i=0;i*m,b=B[i]-A[i]*x,d=gcd(M[i],a);
if(b%d!=0) return make_pair(0,-1); //无解
LL t=b/d*inv(a/d,M[i]/d)%(M[i]/d); //inv求逆元。
x=x+m*t;
m*=M[i]/d;
}
x=(x%m+m)%m; //得到最小的正整数解
return make_pair(x,m);
}