PyTorch学习笔记01: PyTorch基本概念

张量的简介和创建

张量的概念

Tensor与Variable的关系:

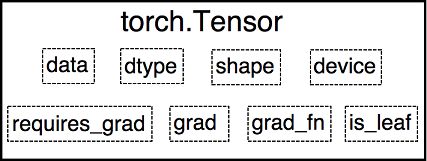
• torch.autograd.Variable封装了Tensor,用于进行自动求导,其属性如下:

  • data: 被包装的Tensor
  • grad: data的梯度
  • grad_fn: 创建Tensor的Function,是自动求导的关键
  • requires_grad: 指示是否需要梯度
  • is_leaf: 指示是否是叶子结点

  

• 从PyTorch0.4.0版开始,Variable并入Tensor,Tensor除Variable原有的属性以外,还有额外的三个属性:

  • dtype: 张量的数据类型,如torch.FloatTensor, torch.cuda.FloatTensor
  • shape: 张量的形状,如(64,3,224,224)
  • device: 张量所在设备,'cpu'或'cuda'

  

张量的创建

有三类创建张量的方式: 直接创建, 依数值创建,依概率创建

创建方式	API
直接创建	torch.tensor() torch.from_numpy(ndarray)
依数值创建	torch.zeros() torch.zeros_like() torch.ones() torch.ones_like() torch.full() torch.full_like() torch.arange() torch.linspace() torch.logspace() torch.eye()
依概率创建	torch.normal() torch.randn() torch.randn_like() torch.rand() torch.rand_like() torch.randint() torch.randint_like() torch.bernoulli() torch.randperm()

直接创建张量

• torch.tensor()

  torch.tensor(data,
               dtype=None,
               device=None,
               requires_grad=False,
               pin_memory=False)
  

  从data创建tensor,参数意义如下:

  • data: 数据,可以是list或NumPy数组
  • dtype: 数据类型,默认与data的一致
  • device: 所在设备,'cpu'或'cuda'
  • requires_grad是否需要梯度
  • pin_memory 是否存于锁页内存

• torch.from_numpy(ndarray)

  从NumPy数组创建Tensor.值得注意的是: 从torch.from_numpy创建的Tensor与原ndarray共享内存,当修改其中一个的数据时,另一个也将会被改动.

  

依数值创建张量

• torch.zeros()

  torch.zeros(*size,
              out=None,
              dtype=None,
              layout=torch.strided,
              device=None,
              requires_grad=False)
  

  依size创建全0张量,参数意义如下:

  • size: 张量的形状,如(3,3),(3,224,224)
  • out: 输出的张量
  • layout: 内存中布局形式,有torch.strided,torch.sparse_coo等

• torch.zeros_like()

  torch.zeros_like(input,
                   dtype=None,
                   layout=None,
                   device=None,
                   requires_grad=False)
  

  依input形状创建全0张量

• torch.ones(),torch.ones_like(): 类似于torch.zeros()和torch.zeros_like()

• torch.full(),torch.full_like():

  torch.full(size,
             fill_value,
             out=None,
             dtype=None,
             layout=torch.strided,
             device=None,
             requires_grad=False)
  

  依input或size形状创建指定数据的张量

  • size: 张量的形状,如(3,3)
  • fill_value: 张量的值

• torch.arange()

  torch.arange(start=0,
      end,
      step=1,
      out=None,
      dtype=None,
      layout=torch.strided,
      device=None,
      requires_grad=False)
  

  创建1维等差数列张量,数值区间为[start,end)左闭右开区间

  • start: 数列起始值
  • end: 数列结束值
  • step: 数列公差,默认为1

• torch.linspace()

  torch.linspace(start,
                 end,
                 steps=100,
                 out=None,
                 dtype=None,
                 layout=torch.strided,
                 device=None,
                 requires_grad=False) 
  

  创建均分的1维张量,数值区间为[start,end]左闭右闭区间

  • start: 数列起始值
  • end: 数列结束值
  • steps: 数列长度

• torch.logspace()

  torch.logspace(start,
                 end,
                 steps=100,
                 base=10.0,
                 out=None,
                 dtype=None,
                 layout=torch.strided,
                 device=None,
                 requires_grad=False)
  

  创建对数均分的1维张量,数值区间为[start,end]左闭右闭区间

  • start: 数列起始值
  • end: 数列结束值
  • steps:数列长度
  • base:对数函数的底，默认为10

• torch.eye()

  torch.eye(n,
            m=None,
            out=None,
            dtype=None,
            layout=torch.strided,
            device=None,
            requires_grad=False)
  

  创建单位对角矩阵,默认为方阵

  • n: 矩阵行数
  • m: 矩阵列数

依概率创建

• torch.normal()

  torch.normal(mean,
               std,
               out=None)
  
  torch.normal(mean,
               std,
               size,
               out=None)
  

  依正态分布生成矩阵

• torch.randn(),torch.randn_like()

  torch.randn(*size,
              out=None,
              dtype=None,
              layout=torch.strided,
              device=None,
              requires_grad=False)
  

  依标准正态分布生成矩阵

• torch.rand(),torch.rand_like(): 依均匀分布生成矩阵

• torch.randint(),torch.randint_like(): 依区间[low, high)内的整数均匀分布生成矩阵

• torch.bernoulli()

  torch.bernoulli(input,
                  *,
                  generator=None,
                  out=None)
  

  以input为概率的伯努利分布生成矩阵

• torch.randperm()

  torch.randperm(n,
                 out=None,
                 dtype=torch.int64,
                 layout=torch.strided,
                 device=None,
                 requires_grad=False)
  

  生成从0到n-1的随机排列

张量的操作

张量的形态变换

形态变换	API
拼接与切分	torch.cat() torch.stack() torch.chunk() torch.split()
张量索引	torch.index_select() torch.masked_select()
形状变换	torch.reshape() torch.transpose() torch.t() torch.squeeze() torch.unsqueeze()

拼接与切分

• torch.cat()

  torch.cat(tensors,
            dim=0,
            out=None)
  

  将张量按维度dim进行拼接

  • tensors: 张量序列
  • dim: 要拼接的维度

• torch.stack()

  torch.stack(tensors,
              dim=0,
              out=None)
  

  将张量在新创建的维度dim上进行拼接

  • tensors: 张量序列
  • dim: 要拼接的维度

torch.cat()和torch.stack()分别在现有维度上和新维度上拼接

t = torch.rand((2, 3))

t_cat = torch.cat([t, t, t, t], dim=1)
t_cat.shape		# torch.Size([2, 12])

t_stack = torch.stack([t, t, t, t], dim=1)
t_stack.shape	# torch.Size([2, 4, 3])

• torch.chunk()

  torch.chunk(input,
              chunks,
              dim=0)
  

  将张量按维度dim进行平均切分,返回张量列表.若不能整除,最后一份张量将小于其它张量

  • input: 要切分的张量
  • chunks: 要切分的份数
  • dim: 要切分的维度

  a = torch.rand((2, 7))  
  list_of_tensors = torch.chunk(a, dim=1, chunks=3)   
  
  for idx, t in enumerate(list_of_tensors):
      print("第{}个张量的形状是 {}".format(idx+1, t.shape))
      
  # 第1个张量的形状是 torch.Size([2, 3])
  # 第2个张量的形状是 torch.Size([2, 3])
  # 第3个张量的形状是 torch.Size([2, 1])
  

• torch.split()

  torch.split(tensor,
              split_size_or_sections,
              dim=0)
  

  将张量按维度dim进行切分

  • tensor: 要切分的张量
  • split_size_or_sections: 为int时,表示每一份的长度;为list时,按list元素切分
  • dim: 要切分的维度

张量索引

• torch.index_select()

  torch.index_select(input,
                     dim,
                     index,
                     out=None)
  

  在维度dim上,按index索引数据,并返回索引结果拼接的张量

  • input: 要索引的张量
  • dim: 要索引的维度
  • index: 要索引数据的序号,数据类型必须为torch.long

  t = torch.randint(0, 9, size=(3, 3))
  idx = torch.tensor([0, 2], dtype=torch.long)    # 索引的数据类型必须为torch.long
  
  t_select = torch.index_select(t, dim=0, index=idx)
  
  # t = tensor([[3, 6, 2],
  #             [0, 1, 2],
  #             [0, 1, 2]])
  # t_select = tensor([[3, 6, 2],
  #         			 [0, 1, 2]])
  

• torch.masked_select()

  torch.masked_select(input,
                      mask,
                      out=None)
  

  按mask中的True进行索引,不论input形状是什么样的,均返回一维张量

  • input: 要索引的张量
  • mask: 与input同形状的布尔类型张量

形状变换

• torch.reshape()

  torch.reshape(input,
                shape)
  

  变换张量形状,值得注意的是: 当张量在内存中连续时,新张量与input共享数据内存.

• torch.transpose()

  torch.transpose(input,
                  dim0,
                  dim1)
  

  交换张量的两个维度

  • input: 要变换的张量
  • dim0: 要交换的维度
  • dim1: 要交换的维度

• torch.t(): 两维张量转置,对矩阵而言,等价于torch.transpose(input, 0, 1)

• torch.squeeze()

  torch.squeeze(input,
                dim=None,
                out=None)
  

  压缩长度为1的维度(轴)

  • dim: 若为None则移除所有长度为1的轴;若指定维度则当且仅当该轴长度为1时才可以被移除.

• torch.unsqueeze()

  torch.usqueeze(input,
                 dim,
                 out=None)
  

  依据dim扩展维度

张量的数学运算

运算类型	API
加减乘除	torch.add() torch.addcdiv() torch.addcmul() torch.sub() torch.div() torch.mul()
指对幂	torch.log(input, out=None) torch.log10(input, out=None) torch.log2(input, out=None) torch.exp(input, out=None) torch.pow()
三角函数	torch.abs(input, out=None) torch.acos(input, out=None) torch.cosh(input, out=None) torch.cos(input, out=None) torch.asin(input, out=None) torch.atan(input, out=None) torch.atan2(input, other, out=None)

• torch.add()

  torch.add(input,
            alpha=1,
            other,
            out=None)
  

  逐元素计算

  $$\text{input}+\text{alpha}\times \text{other}$$

• torch.addcdiv(),torch.addcmul()

  torch.addcmul(input,
                value=1,
                tensor1,
                tensor2,
                out=None)
  

  分别逐元素计算
  $$\begin{gathered} \text{input}+\text{value}\times \frac{\text{tensor1}}{\text{tensor2}} \\ \text{input}+\text{value}\times \text{tensor1}\times \text{tensor2} \end{gathered}$$

计算图与autograde

计算图

计算图的构建和反向传播

计算图是用来描述运算的有向无环图.计算图有两个主要元素: 结点(Node)和边(Edge)

• 结点表示数据,如向量,矩阵,张量
• 边表示运算,如加减乘除卷积等

下图为运算$y=(x+w)\times (w+1)$的计算图:

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-dc8IqIcI-1595936653671)(image-20200728174954681.png)]

使用PyTorch框架构建上述计算图的代码如下:

w = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)

a = torch.add(w, x)  
b = torch.add(w, 1)
y = torch.mul(a, b)

各节点的grad_fn属性记录创建该节点的方法,用于反向传播:

print("w.grad_fn", w.grad_fn)           # w.grad_fn None
print("x.grad_fn", x.grad_fn)           # x.grad_fn None
print("a.grad_fn", a.grad_fn)           # a.grad_fn 
print("b.grad_fn", b.grad_fn)           # b.grad_fn 
print("y.grad_fn", y.grad_fn)           # y.grad_fn 

调用张量y的backward()方法即可进行反向传播,调用节点的grad属性可以查看其梯度

y.backward()
print(w.grad)	# tensor([5.])

叶子节点

不依赖于其他节点的节点被称为叶子节点,张量的is_leaf属性指示张量是否为叶子节点.

print("w.is_leaf:", w.is_leaf)      # w.is_leaf: True
print("x.is_leaf:", x.is_leaf)      # x.is_leaf: True
print("a.is_leaf:", a.is_leaf)      # a.is_leaf: False
print("b.is_leaf:", b.is_leaf)      # b.is_leaf: False
print("y.is_leaf:", y.is_leaf)      # y.is_leaf: False

为节省内存开销,在反向传播结束之后,非叶子节点的梯度会被释放掉:

w = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)

a = torch.add(w, x)  
b = torch.add(w, 1)
y = torch.mul(a, b)

y.backward()
print(w.grad)

print("w.grad:", w.grad)        # w.grad: tensor([5.])
print("x.grad:", x.grad)        # x.grad: tensor([2.])
print("a.grad:", a.grad)        # a.grad: None
print("b.grad:", b.grad)        # b.grad: None
print("y.grad:", y.grad)        # y.grad: None

在执行反向传播以前,调用非叶子节点的retain_grad()方法就可以在反向传播结束之后仍保留该节点的梯度

w = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)
a = torch.add(w, x)  
b = torch.add(w, 1)
y = torch.mul(a, b)
a.retain_grad()
y.retain_grad()

y.backward()
print("w.grad:", w.grad)        # w.grad: tensor([5.])
print("x.grad:", x.grad)        # x.grad: tensor([2.])
print("a.grad:", a.grad)        # a.grad: None
print("b.grad:", b.grad)        # b.grad: tensor([2.])
print("y.grad:", y.grad)        # y.grad: tensor([1.])

autograde自动求导

torch.autograd包下有两个用于自动求导的API,分别对所有节点求梯度和对指定节点求梯度.

• torch.autograd.backward(): 用于对计算图中所有节点求取梯度

  torch.autograd.backward(tensors,
                          grad_tensors=None,
                          retain_graph=None,
                          create_graph=False)
  

  该方法用于对计算图中所有节点求取梯度,每个节点的梯度会累加进该节点的grad属性中

  • tensors: 用于求导的张量,如loss
  • retain_graph: 保存计算图,以便多次重复对该计算图求导
  • create_graph: 创建导数计算图,用于高阶求导
  • grad_tensors：多个梯度的权重

  经过断点调试可以证明,当我们调用计算图中张量的backward()方法时,本质上是在调用``torch.autograd.backward()`方法.

  

• torch.autograd.grad(): 用于求取对指定节点的梯度

  torch.autograd.grad(outputs,
                      inputs,
                      grad_outputs=None,
                      retain_graph=None,
                      create_graph=False)
  

  该方法用于求取计算图中指定节点的梯度,梯度值会直接返回,不会累加进grad属性中

  • outputs: 用于求导的张量,如loss
  • inputs: 需要梯度的张量
  • create_graph: 创建导数计算图,用于高阶求导
  • retain_graph: 保存计算图,以便多次重复对该计算图求导
  • grad_outputs: 多个梯度的权重

通过正确设置上述API的retain_graph参数,可以实现多次重复对计算图反向传播运算.

# 未设置retain_graph参数时,重复反向传播报错
w = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)
a = torch.add(w, x)
b = torch.add(w, 1)
y = torch.mul(a, b)

y.backward()
y.backward()	# RuntimeError: Trying to backward through the graph a second time, but the buffers have already been freed.

# 未设置retain_graph参数时,重复反向传播报错
w = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)
a = torch.add(w, x)
b = torch.add(w, 1)
y = torch.mul(a, b)

y.backward(retain_graph=True)
y.backward()	
print(w.grad)	# tensor([10.]), 两次重复反向传播,梯度累加5*2=10

通过正确设置上述计算图的create_graph参数,可以实现高阶求导

x = torch.tensor([3.], requires_grad=True)
y = torch.pow(x, 2)

grad_1 = torch.autograd.grad(y, x, create_graph=True)	# 计算y对x的一阶导数grad_1,并将grad_1加入计算图
print(grad_1)	# (tensor([6.], grad_fn=),)   grad_1在计算图中,因此存在反向传播函数

grad_2 = torch.autograd.grad(grad_1[0], x)              # 计算y对x的二阶导数grad_2
print(grad_2)	# (tensor([2.]),)

使用自动求导时要注意的问题

1. 梯度不会自动清零,因此在记得在合适的时候将梯度手动清零.

   w = torch.tensor([1.], requires_grad=True)
   x = torch.tensor([2.], requires_grad=True)
   
   for i in range(4):
       a = torch.add(w, x)
       b = torch.add(w, 1)
       y = torch.mul(a, b)
   
       y.backward()
       print(w.grad)
       w.grad.zero_()	# 进入下次循环前将梯度清零
   

2. 依赖于叶子节点的节点,其requires_grad属性默认为True.

3. 参与反向传播的节点应尽量避免in-place操作.

   在PyTorch中,in-place操作的函数通常以下划线_结尾.

   • 对于叶子节点,进行in-place操作时会报错.

     w = torch.tensor([1.], requires_grad=True)
     x = torch.tensor([2.], requires_grad=True)
     
     y = torch.add(w, x)
     w.add_(1)	# 或 w+=1
     # 报错: RuntimeError: a leaf Variable that requires grad is being used in an in-place operation.
     

   • 即使是非叶子节点,如果在构建好计算图后再进行in-place操作,在反向传播时,仍然会报错.

     w = torch.tensor([1.], requires_grad=True)
     x = torch.tensor([2.], requires_grad=True)
     a = torch.add(w, x)
     b = torch.add(w, 1)
     y = torch.mul(a, b)
     
     a.add_(1)	# 在进行反向传播前,对节点进行了in-place操作
     
     y.backward() # 报错: one of the variables needed for gradient computation has been modified by an inplace operation
     

     究其原因,PyTorch框架使用Tensor对象的_version属性来记录版本,每进行一次in-place操作,_version属性加1,若在前向传播和反向传播中某节点的_version属性不匹配,则就会报错.