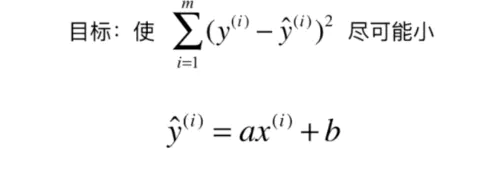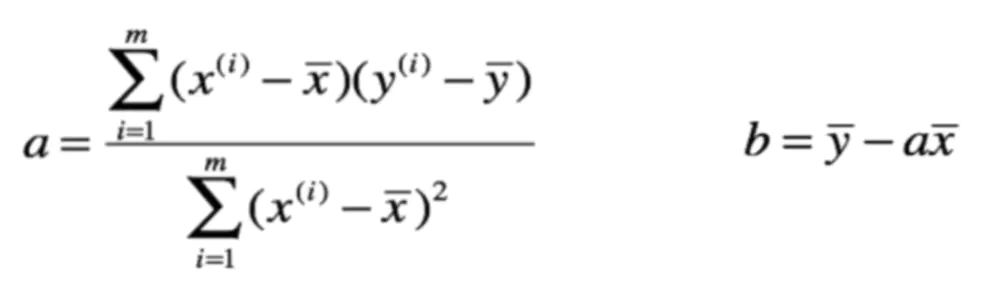简单线性回归

1.线性回归算法简介

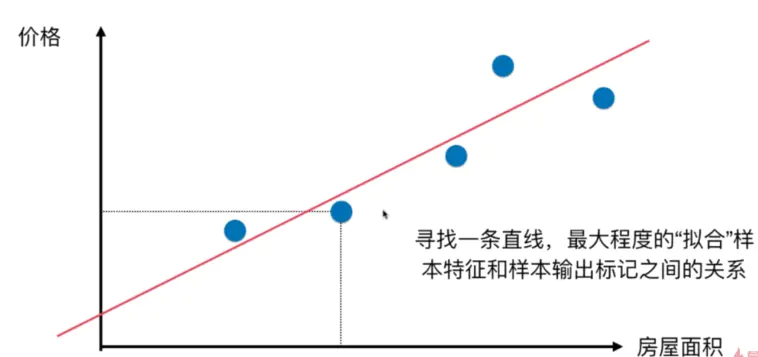
线性回归算法以一个坐标系里一个维度为结果，其他维度为特征（如二维平面坐标系中横轴为特征，纵轴为结果），无数的训练集放在坐标系中，发现他们是围绕着一条执行分布。线性回归算法的期望，就是寻找一条直线，最大程度的“拟合”样本特征和样本输出标记的关系

样本特征只有一个的线性回归问题，为简单线性回归，如房屋价格-房屋面积

将横坐标作为x轴，纵坐标作为y轴，每一个点为（X(i) ,y(i)）,那么我们期望寻找的直线就是y=ax+b，当给出一个新的点x(j)的时候，我们希望预测的y^(j)=ax(j)+b

• 不使用直接相减的方式，由于差值有正有负，会抵消

• 不适用绝对值的方式，由于绝对值函数存在不可导的点

 

 

 

 

a，b参数的求解方法请看我的博客（最小二乘法）。

通过上面的推导，我们可以归纳出一类机器学习算法的基本思路，如下图；其中损失函数是计算期望值和预测值的差值，期望其差值（也就是损失）越来越小，而效用函数则是描述拟合度，期望契合度越来越好

划重点！

2.简单线性回归的实现

2.1 for循环方式实现

• 实现

a,b公式

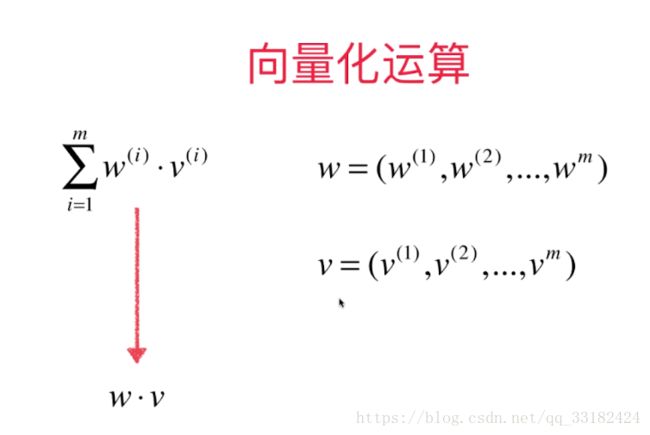
根据上面的推导，我们可以明白为什么a，b的公式要凑成这种形式，是为了利用numpy的特性去进行向量化运算。

import numpy as np
from .metrics import r2_score
class SimpleLinearRegression1:

    def __init__(self):
        """初始化Simple Linear Regression 模型"""
        self.a_ = None
        self.b_ = None

    def fit(self,x_train,y_train):
        """根据训数据集x_train,y_train训练SimpleLinearRegression模型"""
        assert x_train.ndim == 1,  \
            "simple linear regression can only solve single feature training data "
        assert len(x_train) ==len(y_train), \
            "the size of x_train must be equal to the size of y_train"

        x_mean = np.mean(x_train)
        y_mean = np.mean(y_train)

        num = (x_train - x_mean).dot(y_train - y_mean)
        d = (x_train - x_mean).dot(x_train - x_mean)
        self.a_=num / d
        self.b_=y_mean - self.a_ * x_mean
        return self

    def predict(self,x_predict):
        """给定待预测数据集x_predict,返回表示x_predict的结果向量"""
        assert x_predict.ndim == 1, \
            "预测数据集应该是一维的"
        assert self.a_ is not None and self.b_ is not None, \
            "参数a，b不能为空"
        return np.array([self._predict(x) for x in x_predict])

    def _predict(self,x_single):
        """给定单个待预测数据x_single，返回x_single的预测结果值"""
        return self.a_ * x_single + self.b_

    def score(self,x_test,y_test):
        """根据测试数据集x_test和y_test确定当前模型的准确度"""
        y_predict = self.predict(x_test)
        return r2_score(y_test,y_predict)

    def __repr__(self):
        return "SimpleLinearRegression1()"

 向量化实现的性能测试

m = 1000000
big_x = np.random.random(size=m)
big_y = big_x * 2.0 + 3.0 + np.random.normal(size=m)

%timeit reg1.fit(big_x,big_y)
%timeit reg2.fit(big_x,big_y)

    # 输出
    826 ms ± 6.93 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
    11.3 ms ± 84.6 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)

可以看出，向量化的运行速度比循环的形式速度要快80倍