信息安全密码学实验一:古典密码算法的设计与实现
古典密码算法的设计与实现
1.仿射密码
加法密码和乘法密码结合就构成仿射密码,仿射密码的加密和解密算法是:
C=Ek(m)=(k1m+k2)mod n
D=(c-k2)mod n
package czx.xupt.classicalcode;
import java.util.Scanner;
/**
* #Author:槐序二四
* #Time:2019/12/11 14:44
* #Motto:人间荒唐市侩 不如山中作怪.
*/
/**
* 加密过程:e(x) = k1*x + k2 (mod m)
*
* 参数要求:a,m互质;a,b互质;m是集合中元素的个数。(例如当前取1~9和a~z中的所有元素作为集合,m为36)
*/
public class Demo1_Radiationcode {
public static void main(String[] args) {
int m = 36;// m是集合中元素的个数(例如当前取1~9和a~z中的所有元素作为集合,m为36)
int thisNum;
int index = 0;
Scanner s = new Scanner(System.in);
System.out.println("请输入你想加密的内容:");
// 将输入的字符串转化为字符数组
char[] buff = s.nextLine().toCharArray();
// 参数a、b手动输入
System.out.println("输入参数k1,k2:参数k1和36互素,并且参数k1和参数k2互素");
System.out.println("请输入参数k1:");
int k1 = s.nextInt();
System.out.println("请输入参数k2:");
int k2 = s.nextInt();
// 参数要求:a,m互质;a,b互质
while (fun1(m, k1) != 1 || fun1(Math.max(k1, k2), Math.min(k1, k2)) != 1) {
System.out.println("参数不符合要求,请重新输入");
k1 = s.nextInt();
k2 = s.nextInt();
}
for (char i : buff) {
// 由字符转换为数字 (0~36)
if (i > '9'){
//a的asc码是97
thisNum = (int) i - 87;
}else{
thisNum = (int) i - 48; //0的asc码是48
}
// 对该数字加密
thisNum = (thisNum * k1 + k2) % m;
// 加密后再将数字转换为字符
if (thisNum < 10){
buff[index++] = (char) (thisNum + 48);
}else{
buff[index++] = (char) (thisNum + 87);
}
}
System.out.println(buff);
s.close();
}
// 欧几里得算法求两个数的最大公因数
public static int fun1(int a, int b) {
return b == 0 ? a : fun1(b, a % b);
}
}
package czx.xupt.classicalcode;
import java.util.Scanner;
/**
* #Author:槐序二四
* #Time:2019/12/11 14:55
* #Motto:人间荒唐市侩 不如山中作怪.
*/
/**
* 解密过程:d(e(x)) = k1^(-1)*(e(x) - k2) mod m
*/
public class Demo1_DecryptRadiation {
public static void main(String[] args) {
int m = 36;
int thisNum;
int index = 0;
int k;
Scanner s = new Scanner(System.in);
System.out.println("请输入密文:");
char[] buff = s.nextLine().toCharArray();
System.out.println("请输入k1:");
int k1 = s.nextInt();
System.out.println("请输入k2:");
int k2 = s.nextInt();
while (fun1(m, k1) != 1 || fun1(Math.max(k1, k2), Math.min(k1, k2)) != 1) {
System.out.println("参数不符合要求,请重新输入");
k1 = s.nextInt();
k2 = s.nextInt();
}
// k为a模m的逆元
k = fun2(k1, m);
for (char i : buff) {
// 将加密后的字符转换为数字
if (i > '9'){
thisNum = (int) i - 87;
}else{
thisNum = (int) i - 48;
}
// 解密过程 D(E(x)) = a^(-1)*(E(x)-b) mod m
thisNum = ((thisNum - k2) * k) % m;
// 如果结果是负数,则转换为正数,原理为 a % b = (a % b + b) % b
if (thisNum < 0){
thisNum += m;
}
// 最后将解密后的数字转换为字符
if (thisNum < 10){
buff[index++] = (char) (thisNum + 48);
}else{
buff[index++] = (char) (thisNum + 87);
}
}
System.out.println(buff);
}
public static int fun1(int a, int b) {
return b == 0 ? a : fun1(b, a % b);
}
// 循环求a模m的逆元 也就是a乘以一个数%36=1
public static int fun2(int a, int m) {
for (int i = 0; i < m; i++) {
if (a * i % m == 1) {
a = i;
break;
}
}
return a;
}
}


2.置换密码
置换密码算法的原理是不改变明文字符,而是按照某一规则重新排列消息中的比特或字符顺序,才而实现明文信息的加密。置换密码有时又称为换位密码。
package czx.xupt.replacement;
import java.util.Scanner;
/**
* #Author:槐序二四
* #Time:2019/12/25 17:00
* #Motto:人间荒唐市侩 不如山中作怪.
*/
public class Replacement {
public static void main(String[] args) {
System.out.println("请输入明文:");
Scanner sc = new Scanner(System.in);
String s = sc.nextLine();
int len = s.length() % 7 == 0 ? s.length() / 7 : (s.length() / 7) + 1;
char[] chars = new char[7 * len];//将明文存入一维数组
char[][] miwen = new char[len][7];//存放密文的数组
char[][] arr = new char[len][7];//存放明文和解密后的明文
char[] n = new char[7];//消除填充0
int[] key = {
6, 3, 0, 4, 1, 5, 2};//加密密钥
int[] key2 = {
2, 4, 6, 1, 3, 5, 0};//解密密钥
fill(s, chars, len, arr);
encryption(len, miwen, arr, key);
System.out.println("加密后的密文为:");
for (int i = 0; i < len; i++) {
for (int j = 0; j < miwen[i].length; j++) {
System.out.print(miwen[i][j]);
}
}
System.out.println(" ");
System.out.println("解密后的明文为:");
decryption(n, len, miwen, arr, key2, s);
for (int i = 0; i < len; i++) {
for (int j = 0; j < arr[i].length; j++) {
System.out.print(arr[i][j]);
}
}
}
public static void fill(String s, char[] chars, int len, char[][] arr) {
for (int i = 0; i < s.length(); i++) {
chars[i] = s.charAt(i);
}
for (int i = 0; i < chars.length; i++) {
if (chars[i] == '\u0000') {
//判断元素是否为空
chars[i] = '0';
}
}
System.out.println("补充完0并分组的明文内容为:");
for (int i = 0; i < len; i++) {
for (int j = i * 7, k = 0; j < 7 * (i + 1) && k < 7; j++, k++) {
arr[i][k] = chars[j];
System.out.print(arr[i][k]);
}
System.out.println();
}
}
//加密
public static void encryption(int len, char[][] miwen, char[][] arr, int[] key) {
for (int i = 0; i < len; i++) {
for (int j = 0; j < 7; j++) {
miwen[i][j] = arr[i][key[j]];
}
}
}
//解密
public static void decryption(char[] n, int len, char[][] miwen, char[][] arr, int[] key2, String s) {
for (int i = 0; i < len; i++) {
for (int j = 0; j < 7; j++) {
arr[i][j] = miwen[i][key2[j]];
}
}
for (int i = 0; i < 7 - (7 * len - s.length()); i++) {
n[i] = arr[arr.length - 1][i];
}
arr[len - 1] = n;
}
}

3.Hill密码
希尔加密算法的基本思想是,将d个明文字母通过线性变换将它们转换为d个密文字母。解密只要作一次逆变换就可以了,密钥就是变换矩阵本身。
package czx.xupt.hillcode;
import java.util.Scanner;
/**
* #Author:槐序二四
* #Time:2019/12/11 17:28
* #Motto:人间荒唐市侩 不如山中作怪.
*/
public class Demo1_HillCode {
public static void main(String[] args) {
/**
* 加密
*/
Scanner scanner = new Scanner(System.in);
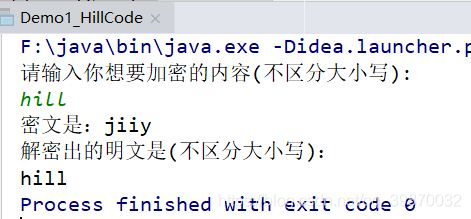
System.out.println("请输入你想要加密的内容(不区分大小写):");
String s = scanner.nextLine();
int[] ints = new int[s.length()];
//将输入的内容转换为0~25
for (int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
ints[i] = (int) c - 97;
}
int[][] getkey1 = Demo1_HillCode.getkey1();
//存储密文的数组
int[] ints1 = new int[4];
//用来接收矩阵运算的结果
int num = 0;
for (int i = 0; i < getkey1.length; i++) {
for (int j = 0; j < ints.length; j++) {
num += ints[j] * getkey1[j][i];
}
ints1[i] = num % 26;
num = 0;
}
System.out.print("密文是:");
for (int i : ints1) {
System.out.print((char) (i + 97));
}
/**
* 解密
*/
int[][] getkey2 = Demo1_HillCode.getkey2();
//用来接收矩阵运算的结果
int num1 = 0;
//用来接收明文的数组
int[] ints2 = new int[4];
for (int i = 0; i < getkey2.length; i++) {
for (int j = 0; j < ints1.length; j++) {
num1 = num1 + ints1[j] * getkey2[j][i];
}
ints2[i] = num % 26;
num = 0;
}
//打印前先换行
System.out.println();
System.out.println("解密出的明文是(不区分大小写):");
for (int anInt : ints) {
System.out.print((char) (anInt + 97));
}
}
public static int[][] getkey1() {
int[][] ints1 = {
{
8, 6, 9, 5},
{
6, 9, 5, 10},
{
5, 8, 4, 9},
{
10, 6, 11, 4}
};
return ints1;
}
public static int[][] getkey2() {
int[][] ints2 = {
{
23, 20, 5, 1},
{
2, 11, 18, 1},
{
2, 20, 6, 25},
{
25, 2, 22, 15}
};
return ints2;
}
}