UCB算法
UCB在做EE(Exploit-Explore)的时候表现不错,但是一个不关心组织的上下文无关(context free)bandit算法,它只管埋头干活,根本不观察一下面对的都是些什么样的arm。
UCB算法要解决的问题是:
面对固定的K个item(广告或推荐物品),我们没有任何先验知识,每一个item的回报情况完全不知道,每一次试验要选择其中一个,如何在这个选择过程中最大化我们的回报?
UCB解决这个Multi-armed bandit问题的思路是:用置信区间。置信区间可以简单地理解为不确定性的程度,区间越宽,越不确定,反之亦反之。
每个item的回报均值都有个置信区间,随着试验次数增加,置信区间会变窄(逐渐确定了到底回报丰厚还是可怜)。
每次选择前,都根据已经试验的结果重新估计每个item的均值及置信区间。
选择置信区间上限最大的那个item。
“选择置信区间上界最大的那个item”这句话反映了几个意思:
- 如果item置信区间很宽(被选次数很少,还不确定),那么它会倾向于被多次选择,这个是算法冒风险的部分;
- 如果item置信区间很窄(备选次数很多,比较确定其好坏了),那么均值大的倾向于被多次选择,这个是算法保守稳妥的部分;
- UCB是一种乐观的算法,选择置信区间上界排序,如果时悲观保守的做法,是选择置信区间下界排序。
UCB1算法
这里我们介绍一个最常见的bandit策略--UCB1算法,该算法的精神被认为是乐观地面对不确定性:我们首先猜测各臂可能给出的奖励,然后选择那个最高臂,如果实际的奖励较少,我们会尽快地降低对该臂的猜测,反之,我们就尽量多选择这个臂. 这里面的猜测,其实就是对各臂的奖励建立了一个指数,通过动态调整这个指数,我们最终将确定那个期望奖励最高的臂.
UCB1算法: 在前K轮,每臂各选择一次, 在\(t=K,K+1...\)轮:
- 选择指数\(I_i\)最大的臂,其中\(I_i=\bar{x}_i+\sqrt{2\frac{\log t}{n_i}}\),其中\(\bar{x}_i\)是均值,\(n_i\)是臂\(i\)当前累积被选择的次数
- 记录获得的奖励,并更新\(\bar{x}_i\)和\(n_i\)
当UCB1算法被执行时,我们可以确定如下定理,其中\(\Delta_i=\mu^{*}-\mu_i\):
定理: UCB1累积遗憾的期望不超过
\[8\sum_{i:\mu_i\lt \mu^{*}}\frac{\log T}{\Delta_i}+(1+\pi^2/3)(\sum_{j=1}^K \Delta_j)\]
定理的证明我就不在这里列出了,具体可以参考Finite-time Analysis of the Multiarmed Bandit Problem.
我们发现UCB1算法的累积遗憾期望是\(O(\log T)\)的,这是不是就足够了呢? 当然不是,如果最坏情况下的累积遗憾过高,该算法其实是没有意义的.
UCB1最坏情况
定理: 最坏情况下的UCB1累积遗憾不超过\(O(\sqrt{KT\log T})\)
我们通过累积遗憾期望函数分析对其进行简单的证明: 首先,我们对累积遗憾期望进行偏微分,得到
\[\frac{\partial R}{\partial \Delta_i}=\frac{8\log T}{\Delta_i^2}+1+\frac{\pi^2}{3}\]
让它等于0,则有\(\Delta_i=\sqrt{\frac{8\log T}{1+\pi^2/3}}=O(\sqrt{\log T})\),但是这时是\(R\)的一个极小值点\(R=O(K\sqrt{\log T})\).同时,如果我们让\(\Delta_i\)尽可能小的话,\(R\)将变得任意大,但是这时所有的奖励都差不多,所以些时还是极小值. 如果我们让\(\Delta_i\)等于1的话,我们还是得到\(R=O(K\sqrt{\log T})\)
其实,如果我们让\(\Delta_i=\Delta\),这时,累积遗憾期望将会是\(\Delta T\),代入公式可得最坏情况下的累积遗憾为\(O(\sqrt{KT\log T})\)
论文:Finite-time Analysis of the Multiarmed Bandit Problem
各UCB算法的比较
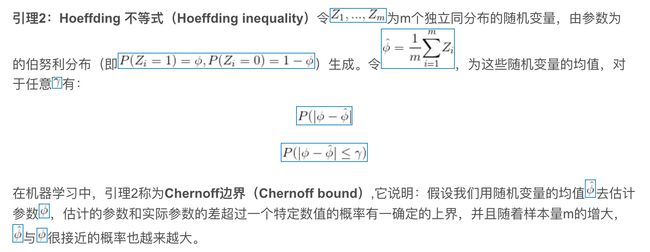
Let be independent, identically distributed random variables, such that and . If , then:
有了先验系数分布和釆样个数就定下后验系数分布,从这来看,另种方法说明为什么总样本数无所谓。
因为我们有\(P(\beta)\) ,有\(P(x_i, i\in [1,n] | \beta), P( \beta | x)\)不就知道了么;
并且决定\(P( \beta | x)\)的interval 的是x(釆样)长度而非总样本长度