路由选择算法
主机通常直接与一台路由器相连接,该路由器即为该主机的默认路由器(defaultrouter) ,又称该主机的第一跳路由器(first-hop router)每当主机发送一个分组时,该分组被传送给它的默认路由器。
源主机的默认路由器称作源路由器(sourcerouter) ,目的主机的默认路由器称作目的路由器(destination router)。
一个分组从源主机到目的主机的路由选择问题显然可归结为从源路由器到目的路由器的路由选择问题。
路由选择算法可分为:
- 全局式路由选择算法:所有路由器掌握完整的网络拓扑和链路费用信息,例如链路状态(LS)路由算法
- 分散式路由选择算法;路由器只掌握物理相连的邻居以及链路费用,例如距离向量(DV)路由算法
又可以分为:
- 静态路由算法:手工配置、路由更新慢、优先级高
- 动态路由算法:路由更新快、定期更新、及时响应链路费用或网络拓扑变化
还可以分为:
- 负载敏感算法:链路费用会动态地变化以反映出底层链路的当前拥塞水平。如果当前拥塞的一条链路与高费用相联系,则路由选择算法趋向绕开该拥塞链路来选择路由。
- 负载迟钝算法:当今的因特网路由选择算法(如RIP 、OSPF和BGP) 都是负载迟钝的,因为某条链路的费用不明显地反映其当前/最近的拥塞水平。
链路状态路由选择算法可以用Dijksua算法实现。
Dijksua算法详见https://www.cnblogs.com/yangyuliufeng/p/9287511.html
所有结点(路由器)通过链路状态广播掌握网络拓扑和链路费用,拥有相同信息,只计算自己的转发表
计算从一个源结点到达所有其他结点的最短路径,经过k次迭代后,得到到达k个目的结点的最短路径
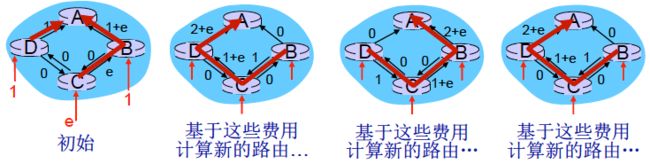
假设链路费用是该链路承载的通信量,则存在震荡(oscillations)可能:
距离向量路由选择算法可以用Bellman-Ford方程dx(y) = min {c(x,v) + dv(y)}实现。
Bellman-Ford算法详见https://www.cnblogs.com/yangyuliufeng/p/9287527.html
每个结点当DV变化时将自身DV估计通告给邻居;邻居在必要时(其DV更新后发生改变)才通告它们的邻居
当结点检测到本地链路费用改变或者接收到来自邻居的新DV估计更新时,即依据B-F方程更新自身的距离向量估计
Dx(y) ← minv{c(x,v) + Dv(y)} for each node y ε N
Dx(y)将最终收敛于实际的最小费用dx(y)
当链路费用变化时:
- 链路费用变小,消息传递快
(1)y检测到链路费用改变 ,更新DV,通告其邻居.
(2)z收到y的DV更新,更新其距离向量表,计算到达x的最新最小费用,更新其DV,并发送给其所有邻居.
(3)y收到z的DV更新,更新其距离向量表,重新计算y的DV未发生改变,不再向z发送DV
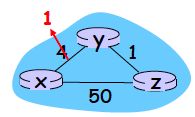
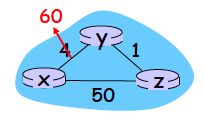
- 链路费用增加,消息传递慢,还会产生无穷计数问题
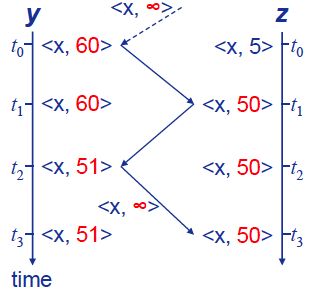
毒性逆转(poisoned reverse):如果一个结点Z到达某目的X的最小费用路径是通过某个邻居Y,则Z告知邻居结点Y到达该目的X的距离为无穷大。使用毒性逆转前后的消息传递过程如图所示:
涉及3个或更多结点(而不只是两个直接相连的邻居结点)的环路将无法用毒性逆转技术检测到。
可以定义最大度量(maximum metric):一个最大的有效费用值,如16跳步表示费用为∞
LS算法和DV算法的比较:
- 报文复杂性
LS 算法要求每个结点都知道网络中每条链路的费用,要发送O(|N|*|E|)个报文。而且无论何时一条链路的费用改变时,必
须向所有结点发送新的链路费用。
DV算法要求在每次迭代时,在两个直接相连邻居之间交换报文。当链路费用改变时,DV 算法仅当在新的链路费用导致与该链路相连结点的最低费用路径发生改变时,才传播已改变的链路费用。
- 收敛速度
LS算法的实现是一个要求O(|N|*|E|)个报文的O(|N|^2)算法。
DV 算法收敛较慢,且在收敛时会遇到路由选择环路,还会遭遇无穷计数的问题。
- 健壮性。
如果一台路由器发生故障、行为错乱或受到破坏时
LS算法:路由器能够向其连接的一条链路广播不正确费用。作为LS广播的一部分,一个结点也可损坏或丢弃它收到的任何LS广播分组。但是每个LS结点都仅计算自己的转发表。因此路由计算在某种程度上是分离的,提供了一定程度的健壮性。
DV算法:一个结点可向任意或所有目的结点通告其不正确的最低费用路径。因此一个不正确的结点计算值会扩散到整个网络。