LeetCode1143动态规划详解！

LeetCode1143 最长公共子序列

1. 问题描述

给定两个字符串 text1 和 text2，返回这两个字符串的最长公共子序列。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。
例如，“ace” 是 “abcde” 的子序列，但 “aec” 不是 “abcde” 的子序列。两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列。

若这两个字符串没有公共子序列，则返回 0。

示例 1:
输入：text1 = “abcde”, text2 = “ace”
输出：3
解释：最长公共子序列是 “ace”，它的长度为 3。

示例 2:
输入：text1 = “abc”, text2 = “abc”
输出：3
解释：最长公共子序列是 “abc”，它的长度为 3。

2. （吹水）

最长公共子序列（Longest Common Subsequence，简称 LCS）是一道非常经典的面试题目，也是一道老典型动态规划了，原型是“0-1背包问题”。使用“动态规划”解决问题的思路是“以空间换时间”，即我们常说的，填表格！！！（这波呀，老动态规划了）

动态规划：
动态规划方法并不是什么高大上的方法可以直接解决问题，而是让我们去寻找原始问题（或者和原始问题差不多）的最初的样子，通过“状态转移方程”记录每一步求解的结果，一步一步解决，最后迎娶白富美走上人生巅峰。

一般来讲，使用动态规划有5个步骤：
1）定义状态
2）思考初始化
3）思考输出
4）思考状态转移方程（这一步是最难的）
5）考虑状态压缩（即优化）

3.理性分析

第一步，一定要明确 dp 数组的含义。
对于字符串text1和text2，一般都要构建这样一个dp表。text1=“abcde”，text2=“acez”

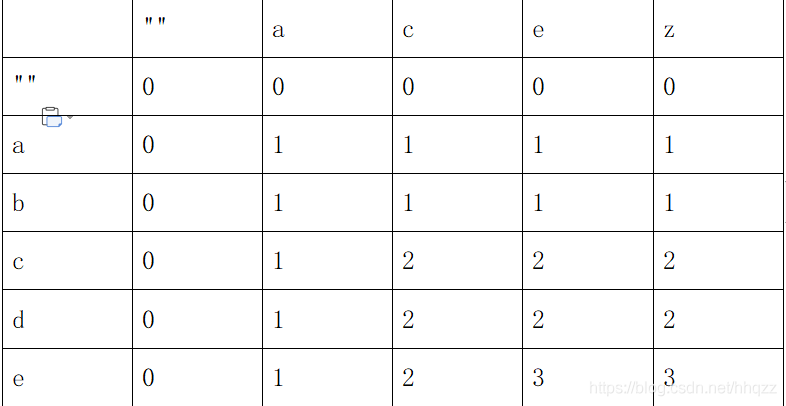
为了方便理解，这里我们约定字符串的索引从1开始。其中dp[i][j]的含义是：对于s1[1,i]和s2[1,j]，它们两者的LCS长度为dp[i][j]。比如dp[2][3]=1，即s1=“ab”，s2=“ace”，它们的LCS长度为1。

第二步，思考初始化
我们让索引为0的行和列分别表示当s1为空 or s2为空，因此第一行和第一列都应该初始化为0。

第三步，思考输出
我们的输出应该为表格中的最后一格，即dp[text1.length()][text2.length()]

第四步，思考状态转移方程（这一步是最难的，希望读者细品）
这道题要求我们求text1和text2的最长公共子序列，那么对于text1和text2中的每一个字符，他们都有两种命运：在LCS中，或者不在LCS中。
text1=“abcde”，text2=“acez”，LCS=“ace”
我们可以注意到，如果某个字符在LCS中，那么他一定存在于 text1 和 text2 中，因此我们需要用两个指针 i 和 j 分别指向 text1 和 text2 ，如果我们发现 text1[i] == text2[j] ，那么这个字符一定在LCS中，即 dp[i][j] = dp[i-1][j-1] + 1 ;
那么如果 text1[i] != text2[j] 呢？就会有三种情况：
1）s1[i]字符在LCS中，s2[j]不在LCS中，比如 text1[3]（c）和 text2[4]（z）比较。此时z不在LCS中。那么此时的LCS应该等价于去 掉text2[4] 这个字符的LCS。说明 ”text1=abc，text2=acez” 和 最长子序列应该和 ”text1=abc，text2=ace” 的最长子序列相等，
即 dp[3][4]=dp[3][3] == dp[i][j] = dp[i][j-1]

2）s1[i]字符不在LCS中，s2[j]在LCS中，比如 text1[4] = d 和 text2[2] = c 比较，此时d不在LCS中。说明" text1 = abcd 和 text2 = ac " 的最长子序列和 " text1=abc，text2 = ac " 相等，即dp[4][2] = dp[3][2]，即 dp[i][j] = dp[i-1][j] 。

3）两个字符都不在LCS中。显然dp[i][j] = dp[i-1][j-1]。（这里不在多述，如有疑问欢迎在评论区提

因此，我们得到了当 text1[i] != text2[j] 的状态转移方程，即
dp[i][j] = max (dp[i-1][j] , dp[i][j-1] , dp[i-1][j-1])

第五步：压缩状态状态方程（即优化）

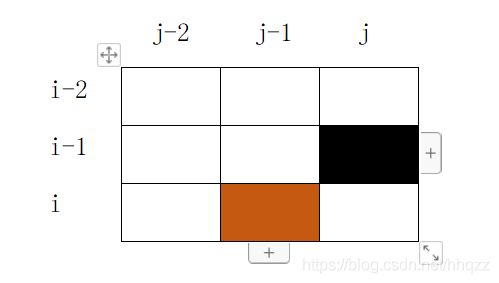
dp[i-1][j] = max( dp[i-1][j-1]，dp[i-2][j] )
即dp[i-1][j] >= dp[i-1][j-1]
同理可得dp[i][j-1] >= dp[i-1][j-1]
也就是说我们在求 dp[i][j] 的时候，不需要再比较 dp[i-1][j-] 了，因为在求前面的 dp[i-1][j] 和 dp[i][j-1] 时，已经比较过了。因此我们的状态转移方程可以进一步优化为：

4. 代码详解

class Solution1143 {
     
    public int longestCommonSubsequence(String text1, String text2) {
     
        if(text1==null || text2==null)
            return 0;
        int n1 = text1.length();
        int n2 = text2.length();
        if(n1==0 || n2==0)
            return 0;
        //dp[i][j]:text1的前i个字符和text2的前j个字符最长的公共子序列
        int[][] dp = new int[n1+1][n2+1];
        for(int i=1;i<=n1;i++){
     
            for(int j=1;j<=n2;j++){
     
                if(text1.charAt(i-1) == text2.charAt(j-1)){
     
                    dp[i][j] = dp[i-1][j-1] + 1;
                }else{
     
                    dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]);
                }
            }
        }
        return dp[n1][n2];
    }
}