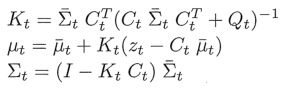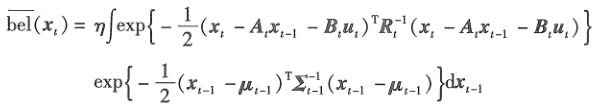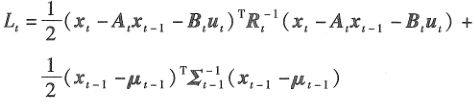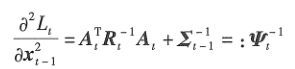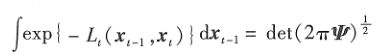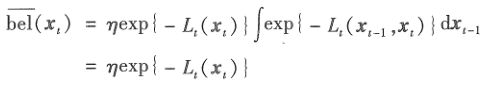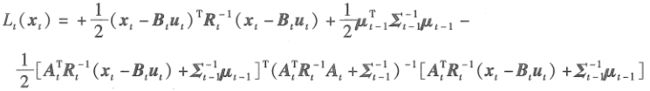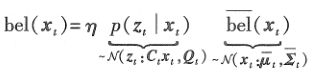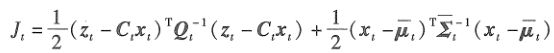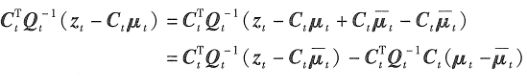概率机器人——卡尔曼滤波

前一篇贝叶斯滤波中提到了贝叶斯滤波不是一种实用的方法，没有办法在计算机中进行表达。是因为贝叶斯是一种抽象的滤波器，其中的置信度表示都是抽象的，没有明确的表达式，没有办法计算积分。尽管如此，贝叶斯给我们提供了一种关于状态最优估计的方法，本篇及后续可能更新的方法皆是贝叶斯滤波的实现方式。

 

---

 

1、高斯滤波

在正式介绍卡尔曼之前，需要先对高斯滤波做一个说明。

高斯滤波是一种递归状态估计器，为了解决贝叶斯滤波器中置信度没有明确表示方法的缺陷，高斯滤波给出了一种置信度用多元正态分布表示的思路，这也是为什么称之为高斯滤波。各种高斯滤波成为连续空间中贝叶斯滤波的有效实现。

置信度用多元正太分布表示：

状态向量x的概率密度用正太分布来表示（即正态分布的均值和方差） ，由于状态是多维的，所以正态分布的均值是一个向量，维数与状态向量维数相同；这里的方差也相应的变成可以衡量多个状态变量同步程度的协方差（后续不再区分，单一变量为方差，多变量为协方差）。

高斯滤波中的参数：均值和方差，称为矩参数。均值为一阶矩，方差为二阶矩。

利用正态分布表示置信度的理解：正态分布的均值即表示最优的状态估计值；方差表示不确定性程度。

 

---

 

2、卡尔曼滤波

 

2.1、线性高斯系统

卡尔曼滤波作为一种线性高斯系统，实现了对连续状态的置信度计算。作为线性系统，为确保后验分布同样是高斯分布，除贝叶斯滤波中的马尔可夫假设之外，还有如下三个假设：

• 状态转移概率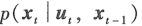必须是带有随机高斯噪声（均值为0，方差为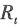）的参数的线性函数：

该状态转移概率称为线性高斯，状态转移函数与其参数呈线性关系，与带有附加高斯噪声的自变量呈线性 。

At为nxn的方阵，n为状态向量的维数；Bt为nxm的矩阵，m为控制向量的维数。

多元正态分布表示如下：

 

• 测量概率与带有高斯噪声的自变量呈线性关系：

向量为测量噪声，均值为0，方差为

多元正态分布表示如下：

 

• 初始置信度必须是正态分布

 

---

 

2.2、卡尔曼滤波算法

卡尔曼源自贝叶斯，完全继承了贝叶斯滤波的思想。整个实现同样包括两部分：控制更新 和 测量更新。

• 控制更新/预测

因为置信度用正态分布表示，所以这里的控制更新，即置信度更新，包括均值和方差更新。

均值更新：根据线性高斯系统的假设1，状态向量用均值向量代替（这个在前面说到了）。

方差更新：通过线性矩阵At，考虑到当前状态依赖前一状态的事实来计算。

 

• 测量更新

测量更新同样需要更新正态分布的均值和方差。除此之外，还多出来一个计算Kt，即卡尔曼增益矩阵的公式，卡尔曼增益矩阵是计算正态分布均值和方差都需要用到的一个参数，它表示测量综合到新的状态估计的程度。

均值更新：根据卡尔曼增益矩阵Kt，真实测量向量与预测测量向量的偏差更新均值。

方差更新：调整由测量引起的信息增益。

 

---

 

2.3、一个例子说明卡尔曼滤波的过程

在证明卡尔曼滤波之前，用《概率机器人》上的一个小例子说明卡尔曼滤波的实现过程。

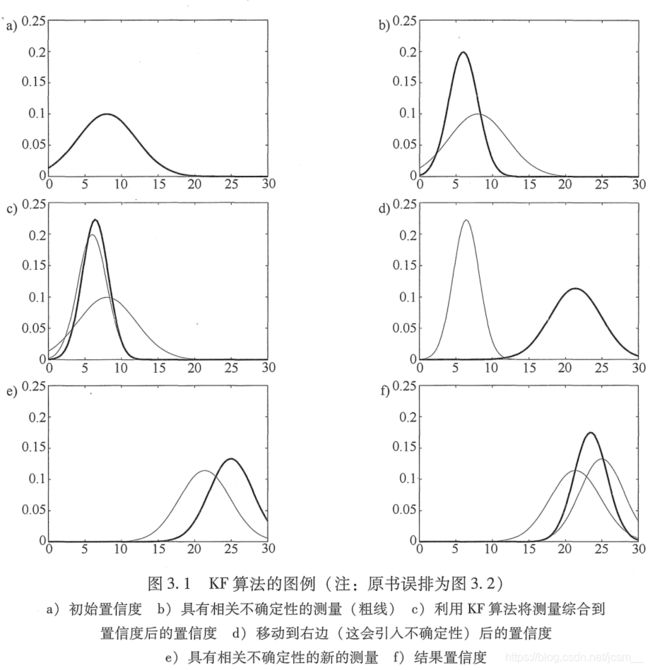
一个一维机器人沿着下图的水平轴移动，机器人上由传感器测量它的位置。图a表示机器人的先验正态分布，图b表示传感器返回的测量值，测量的高斯分布曲线尖峰表示传感器测量值，宽度（方差）表示测量的不确定性程度。后续的过程根据图例的提示可继续进行。

 

---

 

2.4、卡尔曼滤波的数学推导

• 控制更新/预测

根据上篇贝叶斯滤波的控制更新公式来完成卡尔曼滤波控制更新公式的证明，贝叶斯预测如下：

置信度用多元正态分布表示，带入可得：

简写为： 

 其中：

可以看出，积分变量为上一时刻的状态，所以下一步就是将上式进行重新组合，将不含积分变量的和含有积分变量的分离开：

分解的方法不止一种，这部分比较复杂，不再贴出来了，进一步了解可参考《概率机器人》。分解完成后，可得到： 

将常量带入归一化因子（注意：不同位置的归一化因子可能是不同的）：

此时，函数可得出：

展开、计算化简之后可得到：

从上式可以看出，该函数是xt的二次型，所以服从正态分布，分布的均值和方差为的极小值和曲率，据此进行求解一阶导和二阶导，便可得出卡尔曼滤波控制更新的两个公式。

 

---

 

• 测量更新

同样的，先从贝叶斯滤波的测量更新开始：

像控制更新一样，用多元正态分布表示置信度：

其中：

该函数是xt的二次型，因此是一个高斯分布，同样的高斯分布的均值和方差通过求函数的极小值和曲率得到。

一阶导、二阶导：

二阶导的逆（曲率），即的协方差：

令一阶导为0，μt代替xt，计算极小值（均值）：

其中：

带入，得：

定义卡尔曼增益：

将卡尔曼增益表达式，带入均值和方差更新公式，得到：

到此，完成卡尔曼的测量更新推导。

 

---

 

**参考书籍：《概率机器人》