线性回归：最小二乘法优化

一、线性回归

  给定由n个属性描述的样本x=(x0, x1, x2, … , xn)，线性模型尝试学习一个合适的样本属性的线性组合来进行预测任务，如：f(x) = w1x1 + w2x2 + … + wnxn + b = w.T @ x + b。通过一定方法学得向量w和常数b后，模型便可以确定下来。
  而对于给定数据集D={(x1, y1), (x2, y2), … (xm, ym)}，xm=(x1, x2, …, xn)，线性回归则尝试学得一个线性模型来尽可能准确地预测样本的真实输出标记。

func

w1

w2

...

wn

sum

Output

x1

x2

...

xn

  线性模型尝试学得f(x)=wx + b，使f(x)尽可能逼近样本x对应的真实标记y，而这个所谓的逼近程度则可以使用均方误差（Mean Square Error，MSE）来进行衡量：
$$E=\sum _{i=1}^m(f(x_i)-y_i{)}^2$$
  E越小，则模型对真实标记的拟合程度越好，所以线性回归的参数W，b的求解便可以转化为求解以下函数：
$$(w^{\ast },b^{\ast })=\mathrm{argmin}E$$

二、最小二乘法

  前面已经提到过了，线性回归模型建立的关键就是求解：
$$(w^{\ast },b^{\ast })=\mathrm{argmin}E$$
  求解w，b使E最小化的过程，称为线性回归模型的最小二乘“参数估计”（parameter estimation）。我们将E分别对w和b求偏导：
$$\frac{\partial E}{\partial w}=2(W\sum _{i=1}^m{x}_i^2-\sum _{i=1}^m(y_i-b)x_i)$$
$$\frac{\partial E}{\partial b}=2(mb-\sum _{i=1}^m(y_i-w{x}_i))$$
  然后令上述两个式子为0则可以求得w和b最优解的闭式解：
$$w=\frac{{\sum }_{i=1}^m{y}_i(x_i-\overline{x})}{{\sum }_{i=1}^m{x}_i^2-\frac{1}{m}({\sum }_{i=1}^m{x}_i{)}^2}$$
$$b=\frac{1}{m}\sum _{i=1}^m(y_i-w{x}_i)$$
  上述闭式解的推导过程如下：

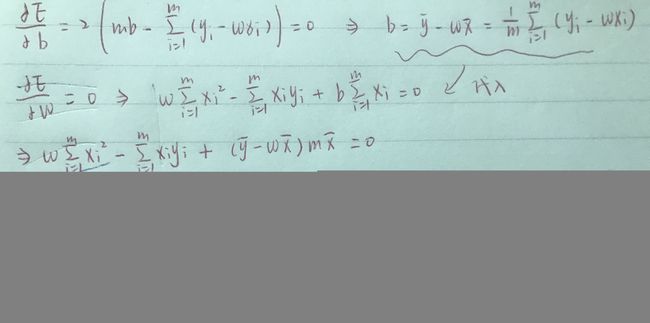
  通过上述推导出的闭式解求解出参数w和b便可以确定最终的线性回归模型。

三、最小二乘法（向量表示）

  在机器学习中常常以向量和矩阵的形式来进行计算从而提高模型的效率，所以这里再讲讲最小二乘法的向量表示。为了便于推导，这里将b合并进入w，并在X中添加了常数列。此时，均方误差的表示变成了：
$$E=(y-Xw{)}^T(y-Xw)$$
  求解：
$$w=\mathrm{argmin}E$$
  这里涉及矩阵求导，所以先介绍两个常用的矩阵求导公式：
$$\frac{\partial A^{T}X}{\partial X}=A\frac{\partial X^{T}X}{\partial X}=2X$$
  现在将E 对w求导：
$$\frac{\partial E}{\partial w}=\frac{\partial E}{\partial (y-Xw)}\frac{\partial (y-Xw)}{\partial w}=2(y-Xw)(-X^T)=2X^T(Xw-y)$$
  令上述导数为0便可以求出w最优解的闭式解。但是需要注意的是，此处涉及了矩阵求逆的运算，所以需要进行简单的讨论。
1）若$X^{T}X$为满秩矩阵或者正定矩阵，则可以求得：
$$w=(X^{T}X{)}^{-}{X}^{T}y$$
2）若$X^{T}X$不是满秩矩阵，例如特征数量大于样本数量时，便可以解出多个w，此时便需要从中选择出一个解来作为模型的参数。

四、Python实现

import numpy as np

class LinearRegression(object):
    def __init__(self):
        self.W = None

    def _linear_func(self, X):
        return X @ self.W[1:] + self.W[0] # z = w0 + w1 * x1 + w2 * x2... = W.T @ x

    def _least_square(self, X, y):
        X0 = np.ones((X.shape[0], 1))
        X = np.hstack([X0, X])
        self.W = np.linalg.inv(X.T @ X) @ X.T @ y # W = (X.T @ X)^-1 @ X.T @ y

    def fit(self, X, y):
        self._least_square(X, y)
        return self

    def predict(self, X):
        return self._linear_func(X)

  导入波士顿房价数据集进行测试：

if __name__ == "__main__":
    from sklearn import datasets
    from sklearn.model_selection import train_test_split
    from sklearn.preprocessing import MinMaxScaler
    from sklearn.metrics import mean_squared_error
    boston = datasets.load_boston()
    X = boston.data
    y = boston.target
    scaler = MinMaxScaler().fit(X)
    X = scaler.transform(X)
    X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.7, test_size=0.3)
    lr = LinearRegression().fit(X_train, y_train)
    y_pred = lr.predict(X_test)
    print(mean_squared_error(y_test, y_pred))
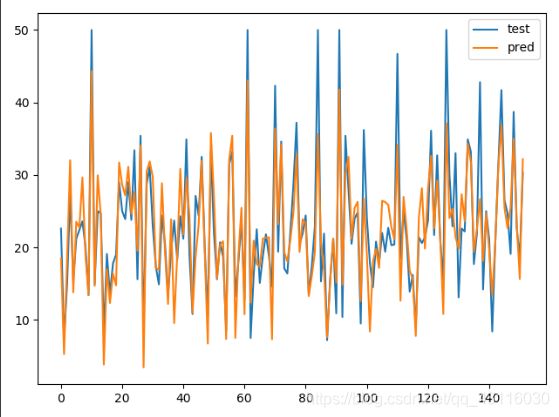
    plt.figure()
    plt.plot(range(len(y_test)), y_test)
    plt.plot(range(len(y_pred)), y_pred)
    plt.legend(["test", "pred"])
    plt.show()

  均方误差：

  拟合曲线：