线段树基础
线段树基础题目
hdu1166 敌兵布阵(单点修改)
标准线段树。对于query中第二行的if为何成立,给个解释。就是left和right表示我们访问的区间,l和r表示我们需要访问的区间,如果访问的区间在我们需要访问的区间内,就直接返回访问区间的值。


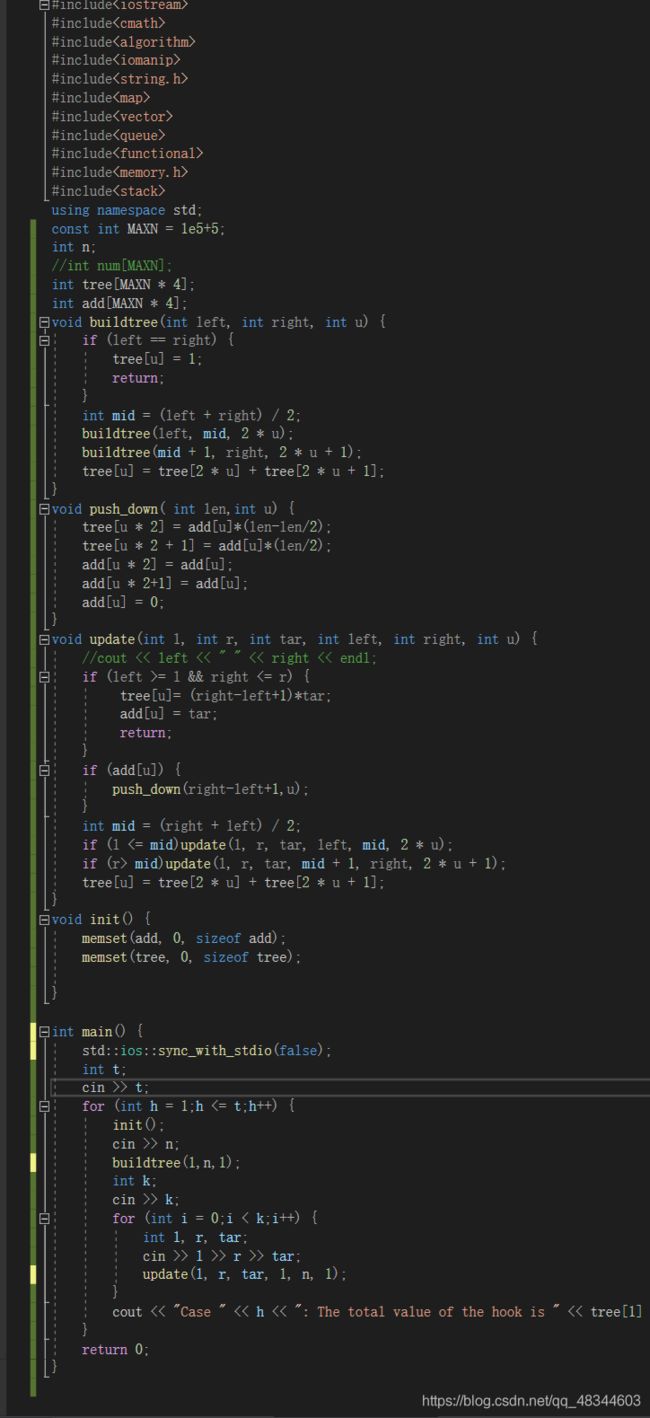
hdu1698 Just a Hook(区间赋值)
区间修改模板题,区间修改比单点修改麻烦点,不过理清思路就行。

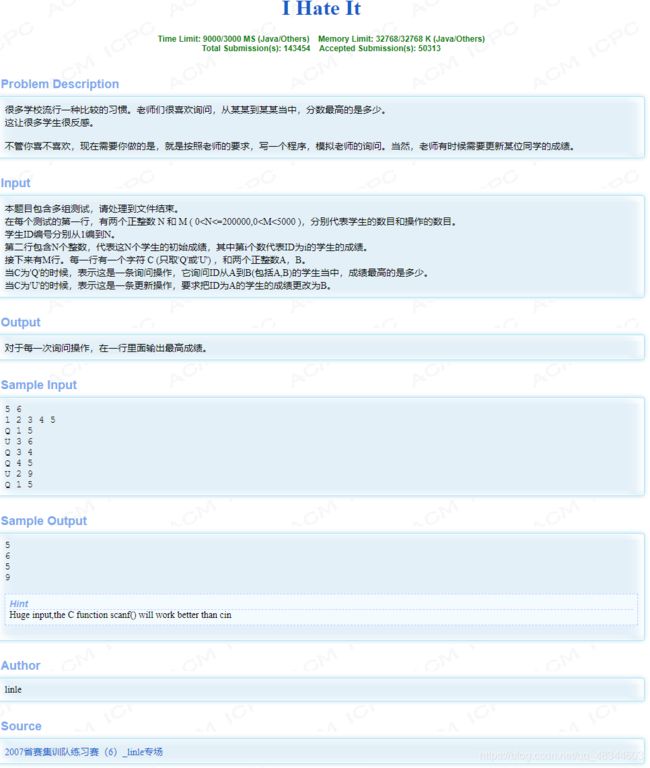
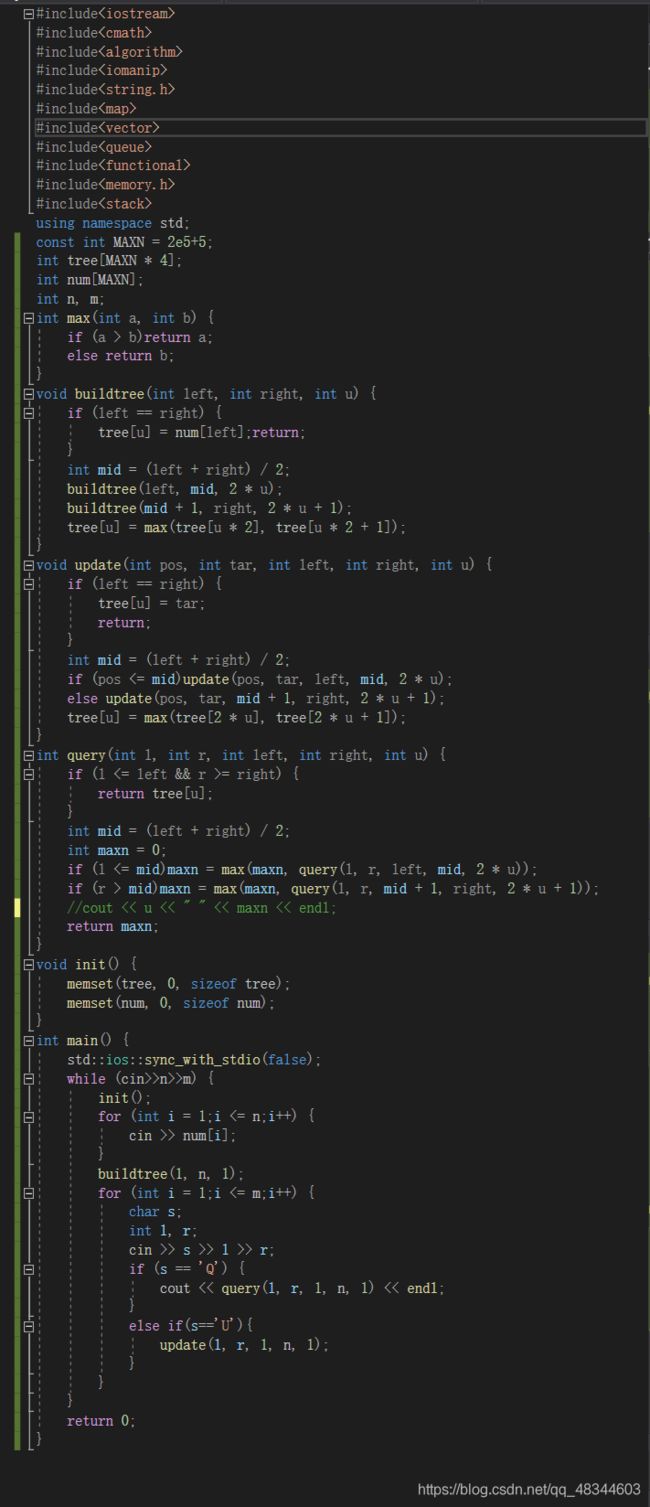
hdu1754 I Hate It(单点赋值)
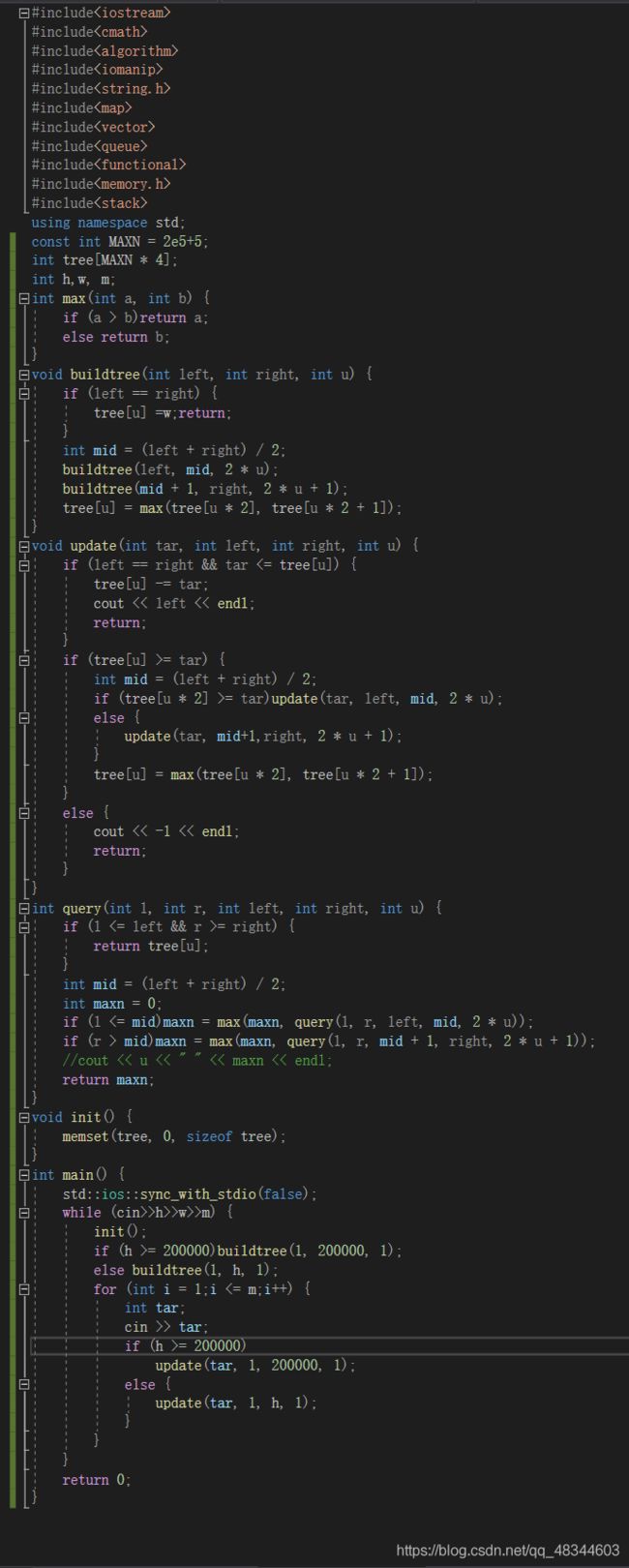
hdu2795 Billboard(线段树保证区间不重复与次序优先)
按照高度分配,初始值为w,线段树记录最大值。每次更新从左往右找。如果h大于2e5,那么建树right为2e5,因为n最大就2e5,所以多的h没用。
这里就没必要用query函数,直接在更新时输出就行。

poj Lost Cows(区间不重复与次序优先)

因为这个牛是往前看的,所以我们要从后面遍历。每次遍历到一个点时,把这个点牛的数量减1,因为我们线段树记录的是牛的区间和。每次遍历都会让一个牛确定,所以区间减1。
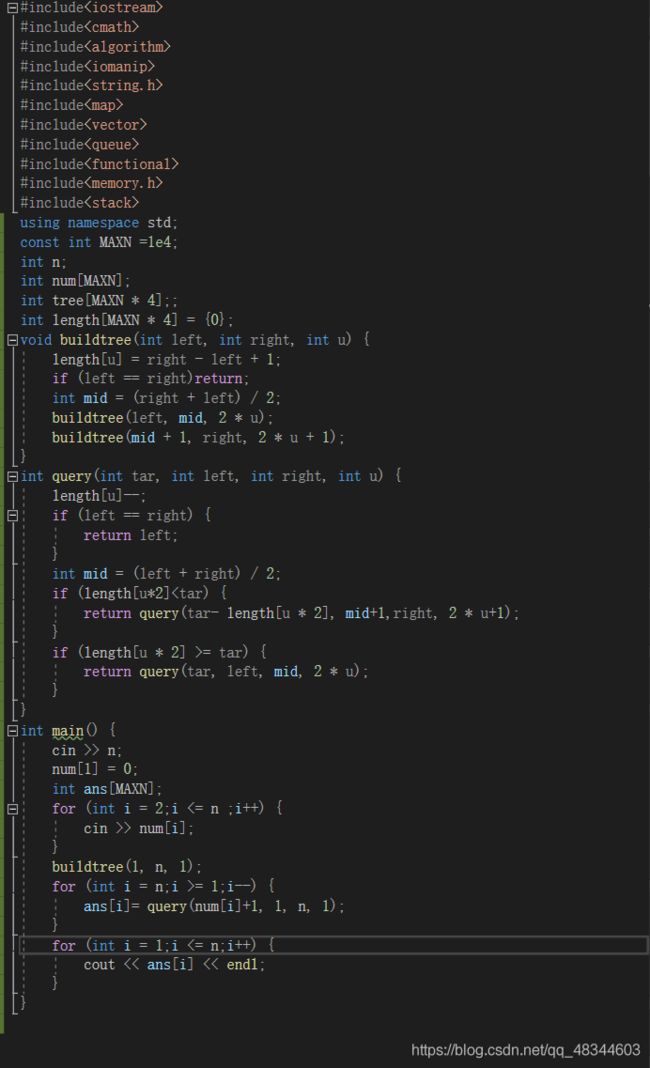
poj2828 Buy Tickets(区间不重复与次序优先)

这题数据比较大,得用结构体,如果直接数组线段树应该会tle。
其次这题和lostcows是一个思路,从后往前,记录位置。

hdu1541 Stars(区间查找小于操作数的数)
因为仔细观察数据,y是递增的,然后我们分析问题其实可以得到,我们要求的就是对于这个点,前面有几个点的x值小于等于它的x值的。再换一种想法就是每次有一个点,我们对线段树就更新这个点。用区间维护这个x的个数,然后到后面统计的时候其实就是求区间和。比如我们对于5 1,我们就是求区间1到5的和。我们1和1就是求1到1的和。

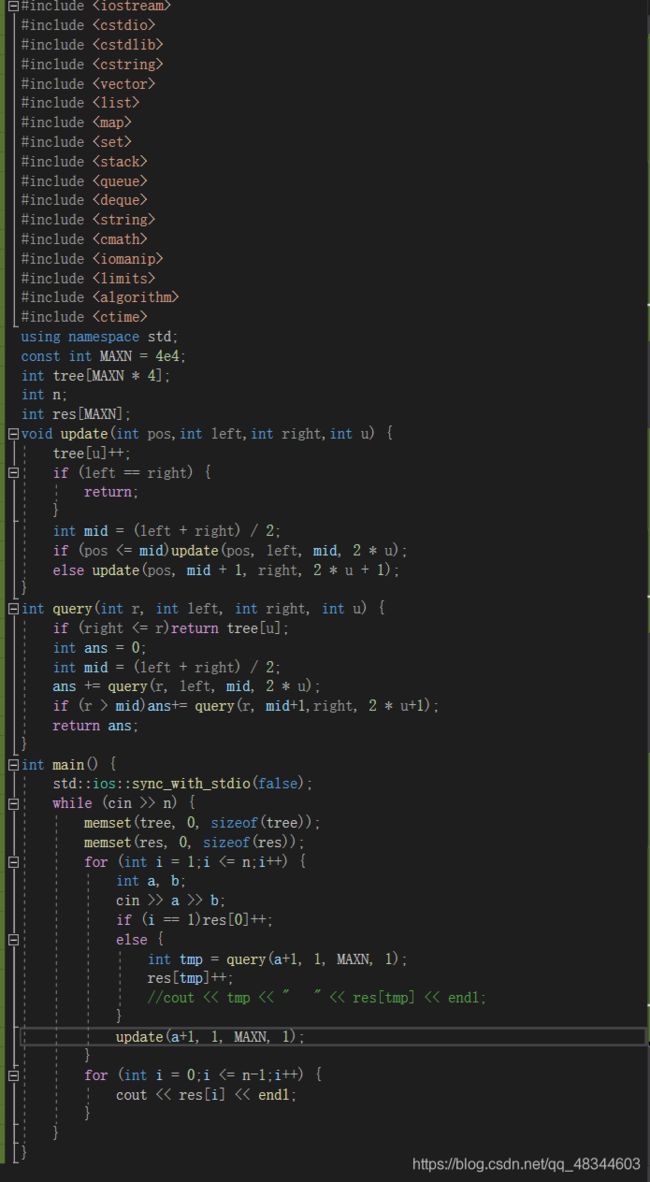
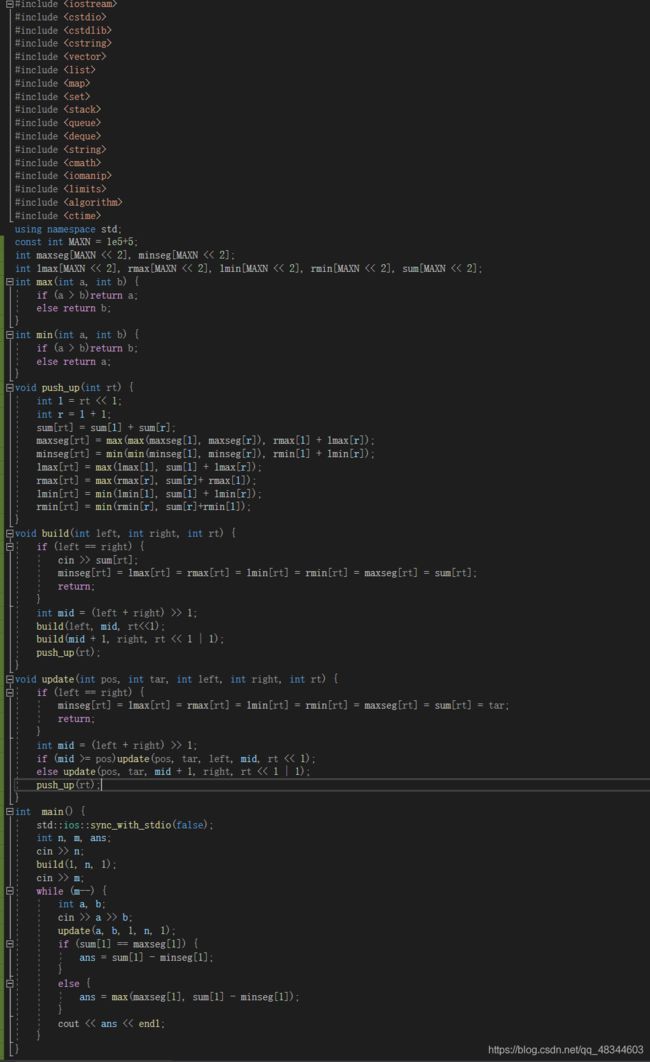
poj2750 Potted Flower(线段树+dp)
这题是区间dp加上线段树。因为是环,所以我们要把它随意切成一个线段。然后求这个线段中连续最大值。那么最大值有哪些情况呢?
一个就是在线段内部,一个就是线段的两边(因为是环,所以可能在线段两头的和是最大值)。对于线段内部,我们定义maxseg维护区间最大值就行,如果是两边的话,我们要用区间和减去最小值minseg。由于有正负数,所以我们还要考虑情况,如果全正数,那么我们maxseg==sum,这时候由于题目知道,我们必须要去掉一个值,那么就让sum-minseg得到,如果有负数,我们可以知道我们至少得去掉一个负数,才会得到 区间最大值。
那么区间最大值该怎么dp到。由于这题有改点操作,所以我们要想到线段树,然后线段树递归是二分的,所以区间最大值可能有左子树,或者右子树,也可能是两者连起来。左右子树最大值很好找,就是maxseg[left]和maxseg[right],但是中间连起来的怎么弄,难道是把这2个maxseg连起来吗?不是, 因为可能中间点有个负数,导致左右子树都不取这个值,导致我们得到的maxseg[rt]中间断开,不是最大连续区间了。所以,我们定义lmax,lmin,rmax,rmin分别用来针对这种情况的最大最小值。对于区间[a,b],lmax表示包含a的最大连续区间,rmax表示包含b的最大连续区间,我们定义left是rt左子树,right是右子树的话,lmax[right]是包含右子树第一个结点的最大连续区间,rmax[left]是包含左子树最后一个结点的最大连续区间,这两个加起来就是包含中间值的最大连续区间。
那么lmax和rmax怎么维护,lmax表示包含a的最大区间的话,对于rt结点,他的lmax[rt]也有2个情况,一个就是lmax[left](这个最大值不包含右子树),另一个是sum[leftt]+lmax[rgiht](这个最大值包含右子树的点,为何要sum,因为lmax定义是包含a的最大连续区间,用sum保证左子树全取到,才能去右子树上的点)其他的同理。

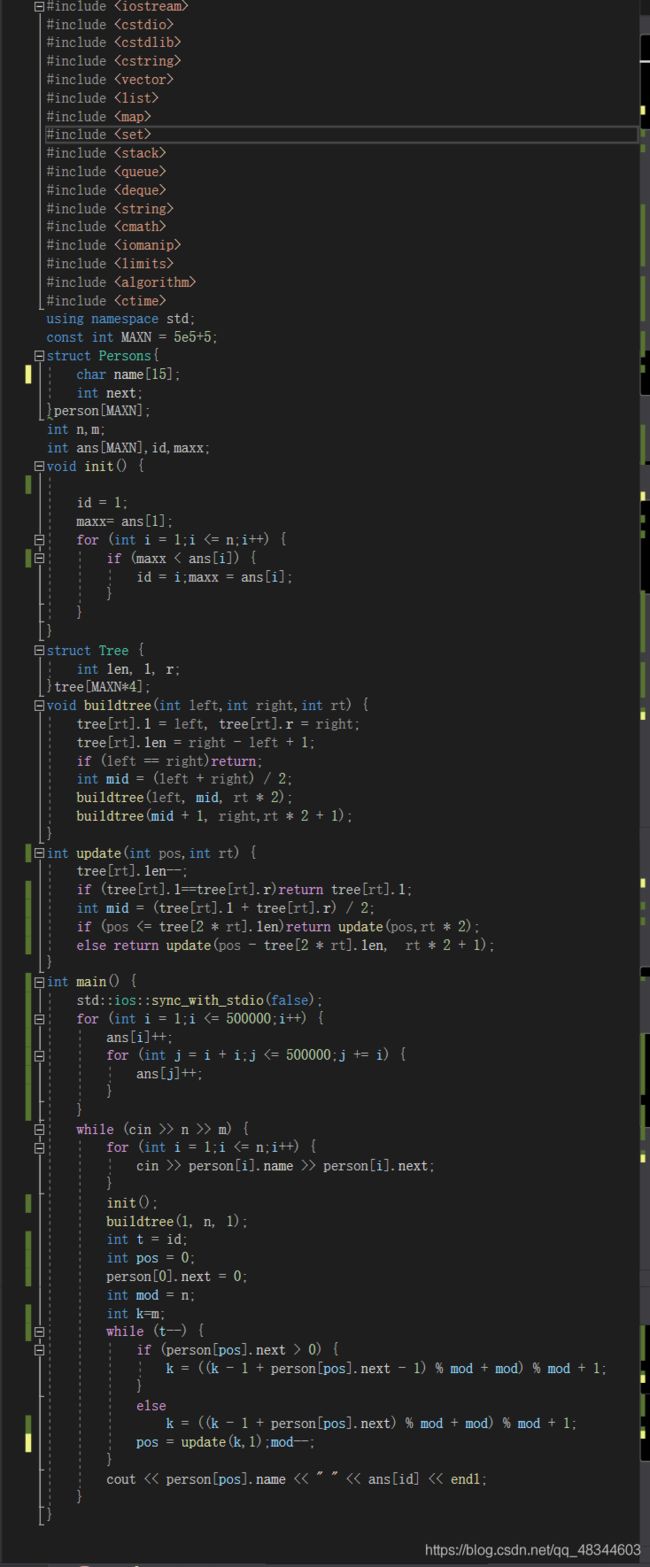
poj2886 Who Gets the Most Candies?(区间不重复与次序优先+约数实现)
这题麻烦的地方:1.分析下一次我们要out哪个位置的孩子。2.如何求约数的数量和。3.怎么避免超时
对于1,我们知道当前位置为k,那么他右边i位置的孩子在线段树上什么位置,(k+i-1)%mod(mod是剩余学生数)为何减一,因为k位置的孩子已经out。对于左边位置i的孩子位置是(k+i)%mod,为何不减一,因为在左边,线段树遍历不会遍历到右边。
对于2,约束一个个求会超时,那么我们整体求,看看这个数是哪些数的约数。
对于3,string函数会超时,建议改为char name[15]。还有就是最好用scanf和printf,时间也相差很多。

poj2777 Count Color(染色性线段树)
染色形线段树。
推荐博客
https://blog.csdn.net/iwts_24/article/details/81603603?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.channel_param&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.channel_param
#include
#include
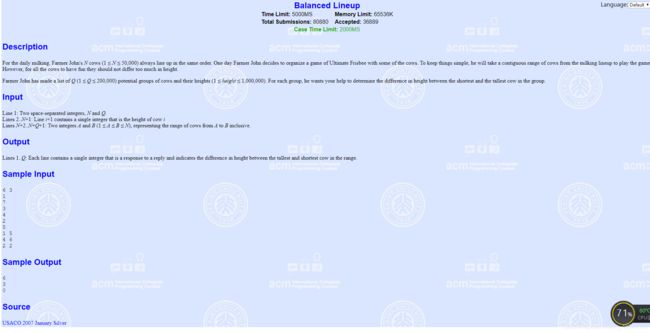
#include poj3264 Balanced Lineup(区间查询,维护双值)
就是求区间最大最小值差,经典线段树只要维护最大值和最小值就行。
#include
#include
#include
cout << maxx - minx << endl;
}
}
poj3468 A simple Problem with integers(区间修改)
#include
#include
#include