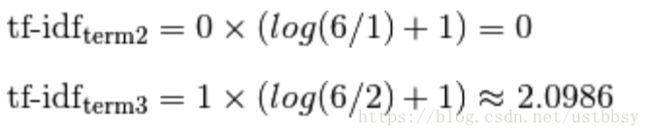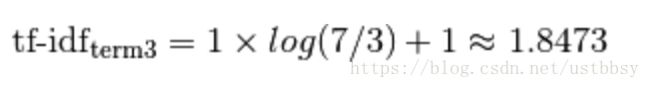TF-IDF详细介绍

1，TF-IDF

tf-idf的基本思想是，有个词出现的频率越高越重要，这个词在其他文档中很少出现，则越有区分度。用来提取关键词

优点：计算速度比较快，通常也符合逾期

缺点：单纯以"词频"衡量一个词的重要性，不够全面，有时重要的词可能出现次数并不多。而且，这种算法无法体现词的位置信息，出现位置靠前的词与出现位置靠后的词，都被视为重要性相同，这是不正确的。（一种解决方法是，对全文的第一段和每一段的第一句话，给予较大的权重。）作者：山的那边是什么_

以上解释来自此处

---

引用百度百科的解释：
TF-IDF是一种统计方法，用以评估一字词对于一个文件集或一个语料库中的其中一份文件的重要程度。字词的重要性随着它在文件中出现的次数成正比增加，但同时会随着它在语料库中出现的频率成反比下降。
TF（Term Frequency）词频：该文章中出现该词的次数除以文章总词数。

     IDF（Inverse Document Frequency）逆向文档词频:IDF=log(D/Dt),即总文章数（D）除以该词出现的文章数（Dt），对商取对数(log)。比例是文章数（Dt）除以总文章数（D），而这里却是D/Dt，这也就是名字中逆的由来。

     TF-IDF=TF*IDF

 例如：在500篇文章中，其中一篇共分得100关键词，其中“大数据”一词出现了10次，那么该词的词频为TF=10/100=0.1；如果该词出现在100篇文章中，那么逆向文档词频为IDF=log(500/100)=1.609；
所以TF-IDF值为
TF-IDF=0.05*1.609=0.08。

关于取对数log，很多博客都没有说清 ‘底数’ 是多少，底为自然对数e
在sklearn中的使用：

from sklearn.feature_extraction.text import TfidfTransformer

参数：

TfidfTransformer(norm=’l2’, use_idf=True, 
smooth_idf=True, sublinear_tf=False)
#norm='l2',类似于l2正则，需要标准化
#平滑参数smooth_idf，在idf等于0的情况下的处理。

如果 smooth_idf=False：
idf(d, t) = log [ n / df(d, t) ] + 1

如果：smooth_idf=True默认
idf(d, t) = log [ (1 + n) / (1 + df(d, t)) ] + 1

来个直观一点的例子：

from sklearn.feature_extraction.text import TfidfTransformer
transformer = TfidfTransformer(smooth_idf=False)
counts = [[3, 0, 1],
        [2, 0, 0],
        [3, 0, 0],
        [4, 0, 0],
        [3, 2, 0],
        [3, 0, 2]]
tfidf = transformer.fit_transform(counts)
print(tfidf.toarray())

结果：

[[0.81940995 0.         0.57320793]
 [1.         0.         0.        ]
 [1.         0.         0.        ]
 [1.         0.         0.        ]
 [0.47330339 0.88089948 0.        ]
 [0.58149261 0.         0.81355169]]

来我们看一下，这个结果是怎么计算的：
假设这是6篇文档，每篇文档只有3个词。
第一篇文档第一个词3开始：
首先计算词频：tf = 3/(3+1) = 0.75
总的文档数等于D = 6，第一篇文档第一个词在这6篇文档中都出现了,Dt = 6
参数是smooth_idf=False， idf(d, t) = log [ n / df(d, t) ] + 1
idf = log(D/Dt) +1 = log(6/6) +1 = 1
tf-idf = 0.75*1=0.75

第一篇文档第2个词0,词频tf = 0, tf-idf = 0
第一篇文档第3个词1, 词频 tf = 1/(1+3)=0.25
总的文档数等于D = 6，第一篇文档第3个词在这6篇文档中出现了2次,Dt = 2
idf = log(D/Dt) +1 = log(6/2) +1 = 2.0986 （底为e）
tf-idf = 0.25 * 2.0986 = 0.52465

然而，我们再看看上面的结果[0.81940995 0. 0.57320793]
和我计算的[0.75 0. 0.52465] 不一样啊
是不是我们计算错了啊？？？
别忘了，我们还有一个参数norm=‘l2’，它的意思是，把我们计算的结果做个调整，标准化。公式如下：

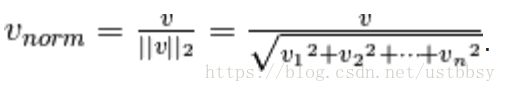
对结果[0.75 0. 0.52465]做个调整：
0.75 --> 0.75/sqrt(0.750.75 + 0. 0.52465 * 0. 0.52465) = 0.8194
0.57320793 --> 0.57320793/sqrt(0.750.75 + 0. 0.52465 * 0. 0.52465) = 0.5732
这里不要偷懒，自己亲手计算一遍，会对tf-idf有更深的理解与记忆。

看一下官方文档的计算：
还是第一篇文档
第一个词3

注意，这里词频计算，直接用原来的数值3，因为有最后一步的标准化，所以不影响最后结果。
同理，计算第2，第3个词的tf-idf：

标准化

对于smooth_idf=True

from sklearn.feature_extraction.text import TfidfTransformer
transformer = TfidfTransformer(smooth_idf=True)
#TF-IDF模型通常和词袋模型配合使用，对词袋模型生成的数组进一步处理
counts = [[3, 0, 1],
        [2, 0, 0],
        [3, 0, 0],
        [4, 0, 0],
        [3, 2, 0],
        [3, 0, 2]]
tfidf = transformer.fit_transform(counts)
print(tfidf.toarray())

结果：

[[0.85151335 0.         0.52433293]
 [1.         0.         0.        ]
 [1.         0.         0.        ]
 [1.         0.         0.        ]
 [0.55422893 0.83236428 0.        ]
 [0.63035731 0.         0.77630514]]

详细的计算过程：
idf的计算公式是下面这一个，分子分母都加1，做了一个平滑

上面计算了，第一个单词的tf-idf = 3

第3个单词的tf-idf为：

最后结果：

2、余弦相似度

余弦相似度，又称为余弦相似性，是通过计算两个向量的夹角余弦值来评估他们的相似度。
说白了，就是计算余弦值
假设向量a、b的坐标分别为(x1,y1)、(x2,y2) 。则：

余弦值的范围在[-1,1]之间，值越趋近于1，代表两个向量的方向越接近；越趋近于-1，他们的方向越相反；接近于0，表示两个向量近乎于正交。
最常见的应用就是计算文本相似度。将两个文本根据他们词，建立两个向量，计算这两个向量的余弦值，就可以知道两个文本在统计学方法中他们的相似度情况。