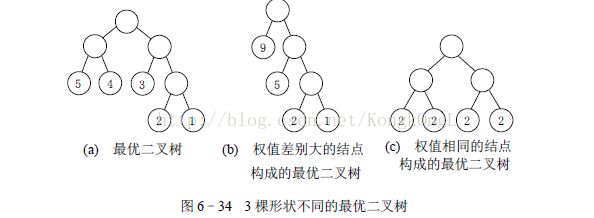
树的形状也各不相同。图634 是3 棵最优二叉树的例子。它们的共同特点是:带权值的
结点都是叶子结点。权值越小的结点,其到根结点的路径越长。构造最优二叉树的方法
如下:
(1) 将每个带有权值的结点作为一棵仅有根结点的二叉树,树的权值为结点的权值;
(2) 将其中两棵权值最小的树组成一棵新二叉树,新树的权值为两棵树的权值之和;
(3) 重复(2),直到所有结点都在一棵二叉树上。这棵二叉树就是最优二叉树。
最优二叉树的左右子树是可以互换的,因为这不影响树的带权路径长度。当结点的权
值差别大到一定程度,最优二叉树就形成了如图634(b)所示的“一边倒”的形状。有些
书称最优二叉树都是这种“一边倒”的形状是不对的。这通过计算二叉树的带权路径长度
是否最短就可看出。当所有结点的权值一样,或其权值差别很小,最优二叉树就形成了如
图634(c)所示的完全二叉树的形状。叶子结点的路径长度近似相等。
最优二叉树除了叶子结点就是度为2 的结点,没有度为1 的结点。这样才使得树的带
权路径长度最短。根据二叉树的性质3,最优二叉树的结点数为叶子数的2 倍减1。
// c6-7.h 赫夫曼树和赫夫曼编码的存储结构(见图6.35)
typedef struct
{
unsigned int weight;
unsigned int parent,lchild,rchild;
}HTNode,*HuffmanTree; // 动态分配数组存储赫夫曼树
typedef char **HuffmanCode; // 动态分配数组存储赫夫曼编码表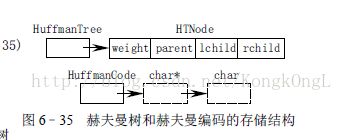
c6-7.h 定义的二叉树结构是我们在前边没有讨论过的,但它特别适合建立赫夫曼树。
赫夫曼树是由多棵二叉树(森林)组合成而的一棵树。这种二叉树结构既适合表示树,也适
合表示森林。赫夫曼树结点的结构包括权值、双亲及左右孩子,双亲值为0 的是根结点,
左右孩子值均为0 的是叶子结点。这种二叉树结构是动态生成的顺序结构。当叶子结点数
确定,赫夫曼树的结点数也确定。由图636(d)可见,建成的赫夫曼树除0 号结点空间不
用外,每个结点空间都没空置。
// func6-1.cpp 程序 algo6-1.cpp和algo6-2.cpp要调用
int min(HuffmanTree t,int i)
{ // 返回i个结点中权值最小的树的根结点序号,函数select()调用
int j,flag;
unsigned int k=UINT_MAX; // 取k为不小于可能的值(无符号整型最大值)
for(j=1;j<=i;j++)
if(t[j].weights2)
{
j=s1;
s1=s2;
s2=j;
}
} // algo6-1.cpp 求赫夫曼编码。实现算法6.12的程序
#include"c1.h"
#include"c6-7.h"
#include"func6-1.cpp"
void HuffmanCoding(HuffmanTree &HT,HuffmanCode &HC,int *w,int n) // 算法6.12
{ // w存放n个字符的权值(均>0),构造赫夫曼树HT,并求出n个字符的赫夫曼编码HC
int m,i,s1,s2,start;
unsigned c,f;
HuffmanTree p;
char *cd;
if(n<=1)
return;
m=2*n-1;
HT=(HuffmanTree)malloc((m+1)*sizeof(HTNode)); // 0号单元未用
for(p=HT+1,i=1;i<=n;++i,++p,++w)
{
(*p).weight=*w;
(*p).parent=0;
(*p).lchild=0;
(*p).rchild=0;
}
for(;i<=m;++i,++p)
(*p).parent=0;
for(i=n+1;i<=m;++i) // 建赫夫曼树
{ // 在HT[1~i-1]中选择parent为0且weight最小的两个结点,其序号分别为s1和s2
select(HT,i-1,s1,s2);
HT[s1].parent=HT[s2].parent=i;
HT[i].lchild=s1;
HT[i].rchild=s2;
HT[i].weight=HT[s1].weight+HT[s2].weight;
}
// 从叶子到根逆向求每个字符的赫夫曼编码
HC=(HuffmanCode)malloc((n+1)*sizeof(char*));
// 分配n个字符编码的头指针向量([0]不用)
cd=(char*)malloc(n*sizeof(char)); // 分配求编码的工作空间
cd[n-1]='\0'; // 编码结束符
for(i=1;i<=n;i++)
{ // 逐个字符求赫夫曼编码
start=n-1; // 编码结束符位置
for(c=i,f=HT[i].parent;f!=0;c=f,f=HT[f].parent)
// 从叶子到根逆向求编码
if(HT[f].lchild==c)
cd[--start]='0';
else
cd[--start]='1';
HC[i]=(char*)malloc((n-start)*sizeof(char));
// 为第i个字符编码分配空间
strcpy(HC[i],&cd[start]); // 从cd复制编码(串)到HC
}
free(cd); // 释放工作空间
}
void main()
{
HuffmanTree HT;
HuffmanCode HC;
int *w,n,i;
printf("请输入权值的个数(>1): ");
scanf("%d",&n);
w=(int*)malloc(n*sizeof(int));
printf("请依次输入%d个权值(整型):\n",n);
for(i=0;i<=n-1;i++)
scanf("%d",w+i);
HuffmanCoding(HT,HC,w,n);
for(i=1;i<=n;i++)
puts(HC[i]);
}
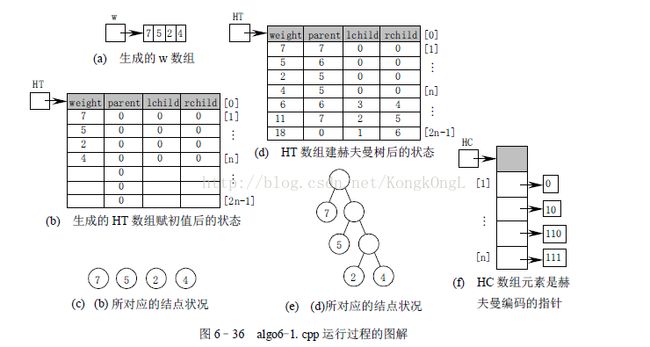
代码的运行结果(以教科书图6.24 为例,如图636 所示):
请输入权值的个数(>1): 4
请依次输入4个权值(整型):
7 5 2 4
0
10
110
111
图636 是运行过程的图解。初始状态下(见图636(b)),权值分别为7、5、2、4
的4 个结点是4 棵独立的树(根结点)。它们没有双亲,也没有左右孩子。反复查找权值最
小的两棵树,并把它们合并成一棵树,其权值为两树的权值之和。最后,所有结点合并成
一棵赫夫曼树(见图636(d))。
算法6.12(在algo6-1.cpp 中)在找到两个无双亲且权值最小的结点后,将序号小的结
点作为左子树,序号大的结点作为右子树,如果不按这个规则,赫夫曼编码的形式会改
变。但码长不会改变,仍然是赫夫曼编码。
// algo6-2.cpp 实现算法6.13的程序
#include"c1.h"
#include"c6-7.h"
#include"func6-1.cpp"
void HuffmanCoding(HuffmanTree &HT,HuffmanCode &HC,int *w,int n) // 前半部分为算法6.12
{ // w存放n个字符的权值(均>0),构造赫夫曼树HT,并求出n个字符的赫夫曼编码HC
int m,i,s1,s2; // 此句与algo6-1.cpp不同
unsigned c,cdlen; // 此句与algo6-1.cpp不同
HuffmanTree p;
char *cd;
if(n<=1)
return;
m=2*n-1;
HT=(HuffmanTree)malloc((m+1)*sizeof(HTNode)); // 0号单元未用
for(p=HT+1,i=1;i<=n;++i,++p,++w)
{
(*p).weight=*w;
(*p).parent=0;
(*p).lchild=0;
(*p).rchild=0;
}
for(;i<=m;++i,++p)
(*p).parent=0;
for(i=n+1;i<=m;++i) // 建赫夫曼树
{ // 在HT[1~i-1]中选择parent为0且weight最小的两个结点,其序号分别为s1和s2
select(HT,i-1,s1,s2);
HT[s1].parent=HT[s2].parent=i;
HT[i].lchild=s1;
HT[i].rchild=s2;
HT[i].weight=HT[s1].weight+HT[s2].weight;
}
// 以下为算法6.13,无栈非递归遍历赫夫曼树,求赫夫曼编码,以上同算法6.12
HC=(HuffmanCode)malloc((n+1)*sizeof(char*));
// 分配n个字符编码的头指针向量([0]不用)
cd=(char*)malloc(n*sizeof(char)); // 分配求编码的工作空间
c=m;
cdlen=0;
for(i=1;i<=m;++i)
HT[i].weight=0; // 遍历赫夫曼树时用作结点状态标志
while(c)
{
if(HT[c].weight==0)
{ // 向左
HT[c].weight=1;
if(HT[c].lchild!=0)
{
c=HT[c].lchild;
cd[cdlen++]='0';
}
else if(HT[c].rchild==0)
{ // 登记叶子结点的字符的编码
HC[c]=(char *)malloc((cdlen+1)*sizeof(char));
cd[cdlen]='\0';
strcpy(HC[c],cd); // 复制编码(串)
}
}
else if(HT[c].weight==1)
{ // 向右
HT[c].weight=2;
if(HT[c].rchild!=0)
{
c=HT[c].rchild;
cd[cdlen++]='1';
}
}
else
{ // HT[c].weight==2,退回
HT[c].weight=0;
c=HT[c].parent;
--cdlen; // 退到父结点,编码长度减1
}
}
free(cd);
}
void main()
{ // 主程序同algo6-1.cpp
HuffmanTree HT;
HuffmanCode HC;
int *w,n,i;
printf("请输入权值的个数(>1): ");
scanf("%d",&n);
w=(int *)malloc(n*sizeof(int));
printf("请依次输入%d个权值(整型):\n",n);
for(i=0;i<=n-1;i++)
scanf("%d",w+i);
HuffmanCoding(HT,HC,w,n);
for(i=1;i<=n;i++)
puts(HC[i]);
}代码的运行结果(以教科书例62 为例):
请输入权值的个数(>1): 8
请依次输入8个权值(整型):
5 29 7 8 14 23 3 11
0110
10
1110
1111
110
00
0111
010